【吴恩达机器学习】第七周课程精简笔记——支持向量机SVM
Support Vector Machines
1. Large Margin Classification
(1)Optimization Objective(优化目标)
对比一下sigmoid函数来看一下

如果我们的 y = 1 y=1 y=1,想要得到 h θ ( x ) ≈ 1 h_\theta(x)≈1 hθ(x)≈1,就需要 让 θ T x ≫ 0 \theta^Tx \gg 0 θTx≫0 。
如果我们的 y = 0 y=0 y=0,想要得到 h θ ( x ) ≈ 0 h_\theta(x)≈0 hθ(x)≈0,就需要 θ T x ≪ 0 \theta^Tx \ll 0 θTx≪0 。

在对数几率回归中,
当 y = 1 y=1 y=1时,令 θ T x ≫ 0 \theta^Tx \gg 0 θTx≫0 , − l o g 1 1 + e ( − x ) -log\frac{1}{1+e^(-x)} −log1+e(−x)1 趋近于0。
当 y = 0 y=0 y=0时,令 θ T x ≪ 0 \theta^Tx \ll 0 θTx≪0 , − l o g 1 1 + e ( − x ) -log\frac{1}{1+e^(-x)} −log1+e(−x)1 趋近于0。
SVM的代价函数是与对数几率回归的代价函数趋向很类似,但SVM的代价函数图像是紫色曲线,由左侧的斜直线和右侧的直线组成。SVM相比于Logistic Regression 有着计算上的优势,并使接下来的优化问题变的更加简单、更容易解决。

在SVM中,我们不再用 λ \lambda λ去控制B,而是用参数 C C C来控制A,使 C A + B CA+B CA+B 整体达到最小。

支持向量机并不会输出一个概率,而是通过一个优化函数得到一个参数,然后使用这个参数来直接预测 y y y 是等于1 还是0。
(2) Large Margin Intuition(大间隔的直观理解)

左右两侧分别为 y = 1 y=1 y=1 和 y = 0 y=0 y=0情况下的函数图像

当我们选择某个参数来将第一项的值变为0时,优化目标就变为
min θ 1 2 ∑ i = 1 n θ j 2 s . t . Θ T x ( i ) ≥ 1 i f y ( i ) = 1 Θ T x ( i ) ≥ 0 i f y ( i ) = 0 \min \limits_{\theta} \frac{1}{2} \sum_{i=1}^n \theta_j^2 \\ s.t. \quad \Theta^Tx^{(i)} ≥ 1 \qquad if \ y^{(i)}=1 \\ \qquad \Theta^Tx^{(i)} ≥ 0 \qquad if \ y^{(i)}=0 θmin21i=1∑nθj2s.t.ΘTx(i)≥1if y(i)=1ΘTx(i)≥0if y(i)=0
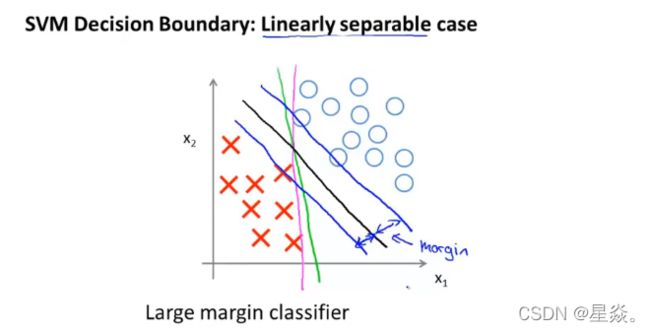
黑色的直线相距正例样本和负例样本具有更大的间隙(margin),在分离样本时,支持向量机会使用尽量可能大的间隙来分离,这使得SVM具有鲁棒性。也因此,SVM有时也称为大间距分类器(a large margin classifier)。
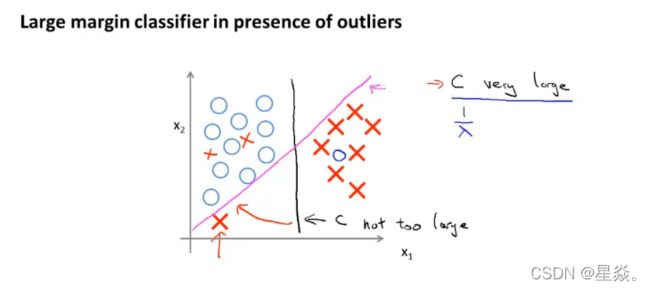
当C被设定值的非常大时,就会对异常点数据非常敏感。间隔线就会由黑色变为紫色。如果C被设置的不是非常大时,它会忽略左下角的异常点,间隔线依然使黑色线。C的作用类似与 1 λ \frac{1}{\lambda} λ1 ,当C非常大或者说 λ \lambda λ 非常小时,拟合能力过强容易出现过拟合现象。当C设置的不是非常大或者说 λ \lambda λ 不是非常小时,就觉有更强的泛化能力,会忽略一些异常点来得到预测结果。甚至于在非线性问题上,SVM也能取到很好的效果。
(3)Mathematics Behind Large Margin Classification
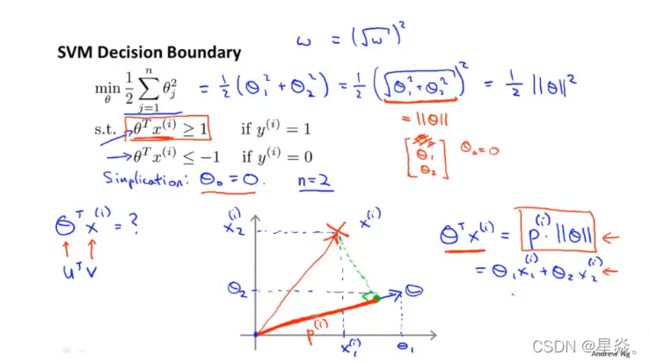
可以将目标优化函数转换为范数形式 1 2 ∣ ∣ Θ ∣ ∣ 2 \frac{1}{2} ||\Theta||^2 21∣∣Θ∣∣2,其中 Θ = [ θ 0 θ 1 θ 2 ] , θ 0 假 设 为 0 \Theta = [ \theta_0 \ \theta_1 \ \theta_2],\theta_0假设为0 Θ=[θ0 θ1 θ2],θ0假设为0。

假设 θ 0 = 0 \theta_0 = 0 θ0=0 的好处是可以让我们的决策边界通过原点,便于观察。当然令 θ 0 \theta_0 θ0 等于其他数也可以不会影响最终结果。
2. Kernels(核函数)
(1)Kernel I

我们使用了一个新的符号f来表示非线性决策边界

手动选取一些点,将其称为 l ( 1 ) 、 l ( 2 ) 、 l ( 3 ) l^{(1)}、l^{(2)}、l^{(3)} l(1)、l(2)、l(3),我们将 f i f_i fi 定义为一种相似度的度量,即训练样本 x x x 和 标记 ( i ) ^{(i)} (i) 之间的相似度。Kernel(核函数,也称高斯核函数)如下:
f i = s i m i l a r i t y ( x , l ( i ) ) = e − ∣ ∣ x − l ( i ) ∣ ∣ 2 2 σ 2 f_i = similarity(x,l^{(i)})=e^{-\frac{|| x - l^{(i)} ||^2}{2\sigma^2}} fi=similarity(x,l(i))=e−2σ2∣∣x−l(i)∣∣2

当训练样本 x x x 与 l ( i ) l^{(i)} l(i) 非常接近时, f 1 ≈ 1 f_1≈1 f1≈1;
当训练样本 x x x 与 l ( i ) l^{(i)} l(i) 距离非常远时, f 1 ≈ 0 f_1≈0 f1≈0。

在这个三维图中,z轴表示 f 1 f_1 f1、另外两个轴表示 x 1 x_1 x1、 x 2 x_2 x2,给定一个 x 1 x_1 x1 和 x 2 x_2 x2 的值,可以得到相应的 f 1 f_1 f1 的值。当 x ⃗ = [ 3 5 ] T \vec{x} = [3 \ 5]^T x=[3 5]T 时, f 1 = 1 f_1 = 1 f1=1,此时正好是最大值。当越偏离这个点时,就会 f 1 f_1 f1 越接近于0。
当改变 σ 2 \sigma^2 σ2 时,将会改变函数的图像。当 σ 2 \sigma^2 σ2变小时,可以发现图像还是相似的,但是整体变窄了。当偏离最大值点时,这个函数接近0值的速度变的更快了。当 σ 2 \sigma^2 σ2变大时,图像整体变宽了。当偏离最大值点时,这个函数接近0值的速度变的更慢了。

令 θ 0 = − 0.5 , θ 1 = 1 , θ 2 = 1 , θ 2 = 0 \theta_0=-0.5, \theta_1 = 1, \theta_2 = 1, \theta_2 = 0 θ0=−0.5,θ1=1,θ2=1,θ2=0
考虑紫色点,会得到 f 1 ≈ 1 , f 2 ≈ 0 , f 3 ≈ 0 f_1≈1,f_2≈0,f_3≈0 f1≈1,f2≈0,f3≈0,从而得到 θ 0 + θ 1 × 1 + θ 2 × 0 + θ 3 × 0 = − 0.5 + 1 = 0.5 ≥ 0 \theta_0+\theta_1 × 1 + \theta_2 × 0 + \theta_3 × 0 = -0.5 + 1 = 0.5 ≥ 0 θ0+θ1×1+θ2×0+θ3×0=−0.5+1=0.5≥0,那么就预测紫色点是 y = 1 y=1 y=1。
考虑蓝色点,会得到 f 1 , f 2 , f 3 ≈ 0 f_1,f_2,f_3≈0 f1,f2,f3≈0,从而得到 θ 0 + θ 1 f 1 + θ 2 f 2 + θ 3 f 3 ≈ − 0.5 < 0 \theta_0 + \theta_1f_1 + \theta_2f_2 + \theta_3f_3 ≈ -0.5 < 0 θ0+θ1f1+θ2f2+θ3f3≈−0.5<0,那么就预测蓝色点是 y = 0 y=0 y=0。
综上可以从直观上认为,接近 l ( 1 ) l^{(1)} l(1) 和 l ( 2 ) l^{(2)} l(2) 的点预测为 y = 1 y=1 y=1,远离 l ( 1 ) l^{(1)} l(1) 和 l ( 2 ) l^{(2)} l(2) 的点预测为 y = 0 y=0 y=0。可以大致得到,红色的那条线为我们的决策判别边界(the decision boundary)。在红色曲线内的值,预测为 y = 1 y=1 y=1,曲线外的预测为 y = 0 y=0 y=0 。
(2)Kernel II

给定核函数和相似度函数

在这个优化函数中,我们有n个特征。而我们的有效特征,也相当于是f的维度的数量,所以n实际上等于m。
和之前的视频一样,我们不会正则化参数 θ 0 \theta_0 θ0,而是从 1 到 m 1到m 1到m,也相当于是从 1 到 n 1到n 1到n。
这就是我们的支持向量机算法,在具体的应用中,最后这一项会有点不同。会用 Θ T M Θ \Theta^TM\Theta ΘTMΘ ,其中 M M M 为我们定义的核函数这种形式来取代后面这一项。这样做可以使它能够应用于更大的训练集上。然而,如果将核函数的方式应用到对数几率回归上将会变得很慢。

C较大,相当于 λ \lambda λ 较小时,会发生过拟合现象。
C较小,相当于 λ \lambda λ 较大时,会发生欠拟合现象。
σ 2 \sigma^2 σ2 较大,高斯核函数,即相似度函数就会非常光滑,会得到一个较大的偏差、较低方差的分类器,过拟合现象。
σ 2 \sigma^2 σ2 较小,特征 f i f_i fi ,高斯核函数的变化就会非常剧烈,会得到一个较大方差、较低偏差的分类器,会发生欠拟合现象。
3. Using an SVM
使用SVM工具包,得到参数 θ \theta θ。
使用的时候需要考虑如下情况:
- 选择参数C
- 选择核函数(你想使用的相似函数)
- 其中一个是选择不使用任何内核参数,这样的函数也称为线性核函数,也就是实现了一个不带核函数的线性SVM。 这是一个只使用了 θ T x \theta^Tx θTx 的核函数。在使用此方法时,要考虑选取样本特征值数和样本数量的均衡。
- 如果你想要使用核函数来拟合相当复杂的非线性决策边界的话,高斯核函数是一个不错的选择。在使用此方法时,要考虑 σ 2 \sigma^2 σ2 的大小。
- 高斯核函数和线性核函数是最常用的两个核函数。

在实现这个核函数前,记得将特征变量的大小按比例进行归一化。

这里还有一些其他的核函数

对于多分类任务,与之前的可相同使用one-vs-all方法,训练K个SVM,分出K个类别。将每个类别从其他类别中区分出来。
第一种情况: n大,m小。如果特征量相对较多而数据集规模相对较小,线性函数可能会工作的很好,你有足够的数据集来拟合非常复杂的非线性函数。
第二种情况: n小,m适中。如果特征量相对较小而数据集规模适中,使用线性核函数的SVM会工作的更好。
第三种情况: n小,m大。如果特征量相对较小而数据集规模相对较大。高斯核函数的运行速度就会很慢。应该手动的创建一些特征变量,然后用对数几率回归或者不带核函数的SVM(这两者都是非常相似的算法)。
对于不同的问题,设计不同的神经网络可能会非常有效,但神经网络训练起来可能会特别慢。相反,如果你有一个好的SVM实现包,那么它将会运行的比较快,比神经网络快很多。
SVM是一个凸优化问题,一个好的SVM实现包总会找到全局最小值或者接近它的值。因此,在使用SVM是,你不用担心局部最优解。
拓展阅读
对于由 w T x + b = 0 \boldsymbol{w^Tx}+b=0 wTx+b=0 公式描述的超平面,实际上是用了高数下里解析几何里的知识,使用点法式方程定义了超平面公式: A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A(x−x0)+B(y−y0)+C(z−z0)=0
平面上点 x \boldsymbol{x} x 到超平面 ( x , b ) (\boldsymbol{x},b) (x,b) 的的距离 r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r=\frac{|\boldsymbol{w^Tx}+b|}{||\boldsymbol{w}||} r=∣∣w∣∣∣wTx+b∣,使用的是高数下的点到平面的距离公式: ∣ A x 1 + B y z + C z 1 + D ∣ A 2 + B 2 + C 2 \frac{|Ax_1+By_z+Cz_1+D|}{\sqrt{A^2+B^2+C^2}} A2+B2+C2∣Ax1+Byz+Cz1+D∣
注意要区分平面公式和直线公式的区别。平面公式是使用法向量和平面上的点定义平面,直线公式是使用方向向量和直线上的点定义直线,不要搞混淆。
SVM笔记1——对SVM中超平面的理解
Exercise 6:支持向量机SVM
【吴恩达机器学习】Week7 编程作业ex6——支持向量机SVM