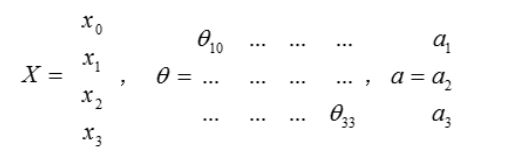吴恩达机器学习——笔记
(考研数学一基础,仅供个人纪录,大纲为主,其中python代码cr [email protected] 笔记)
一、基础知识
1 监督学习/无监督学习
2 单变量线性回归
(1)模型表示
(2)代价函数(cost function)——残差平方和
(3) 直观理解——图示法
(4)梯度下降——求解全局最小值
学习率α;梯度下降算法;梯度下降中的线性回归
正规方程法 ![]() ——向量化
——向量化
3 多变量线性回归
(1)多维特征
(2)多变量梯度下降法
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))①特征缩放——类似于正态分布标准化
②学习率——影响迭代次数和最终收敛
(3)特征和多项式回归
(4)正规方程法(特征变量数目不大时)![]()
import numpy as np
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X 等价于 X.T.dot(X)
return theta不可逆性——伪逆
4 逻辑回归
( Logistic Regression)
①逻辑函数(logistic function ) 或 S型函数(Sigmoid function)
python 代码实现:
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))②判定边界(decision border)
③代价函数——log(有点类似假设检验)
import numpy as np
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
return np.sum(first - second) / (len(X))注:虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样,但是这里 的ℎ() = ()与线性回归中不同,所以实际上是不一样的。另外,在运行梯度下降算法 之前,进行特征缩放依旧是非必要的
④分类:一对多(one-vs-all)—— 逻辑回归分类、取最大值
⑤其他高级优化算法
5 正则化
(Regularization)
(1)原因:过拟合(over-fitting)——无法泛化/推广到新数据
(正则化,就是通过收缩的办法,限制模型变的越来越「大」,牺牲样本内误差,降低模型(参数)的误差,从而提高样本外的预测效果,防止过拟合)
(2)处理办法:正则化——保留所有特征,但是减少参数的大小
(3)代价函数——添加正则化参数![]()
(4)线性回归的正则化
(5)逻辑回归的正则化
import numpy as np
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:the
ta.shape[1]],2))
return np.sum(first - second) / (len(X)) + reg
二、神经网络
(Neutral Network)
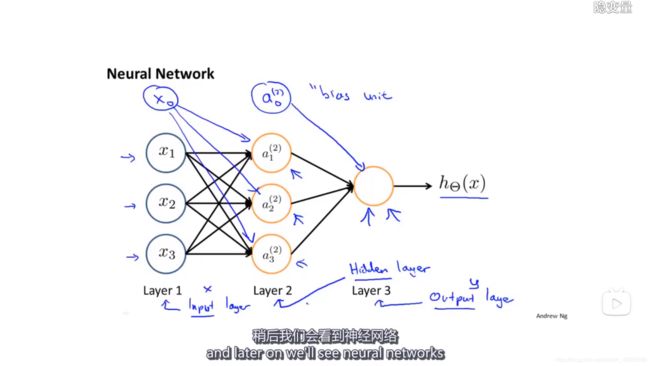
1 表述
(1)神经元/激活单元,activation unit
(2)输入层、隐藏层、输出层、偏差单位(bias unit)
(3)模型表示(前向传播)
![]() 代表第2层的第一个激活单元
代表第2层的第一个激活单元
![]() 代表从第一层映射到第二层的权重的矩阵,其尺寸为:以第j+1层的激活单元数量为行数,以第j层的激活单元加一为列数的矩阵,例如上图所述
代表从第一层映射到第二层的权重的矩阵,其尺寸为:以第j+1层的激活单元数量为行数,以第j层的激活单元加一为列数的矩阵,例如上图所述![]() 的尺寸为3*4
的尺寸为3*4
![]()
(4)举例
①XOR/异或:如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
XNOR/同或:异或结果取反
AND模型、OR模型
②通过上述模型组合构造神经网络——XOR模型
(5)利用神经网络解决多元分类问题
2 学习
(1)反向传播算法
(2)梯度检验(gradient checking)
(3)初始随机化(random initialization)
(4)训练神经网络
1. 参数的随机初始化2. 利用正向传播方法计算所有的 ℎ ()3. 编写计算代价函数 的代码4. 利用反向传播方法计算所有偏导数5. 利用数值检验方法检验这些偏导数6. 使用优化算法来最小化代价函数
(5)改进神经网络算法
①训练集:交叉验证集:测试集=6:2:2
②诊断偏差和方差(d—特征数量)
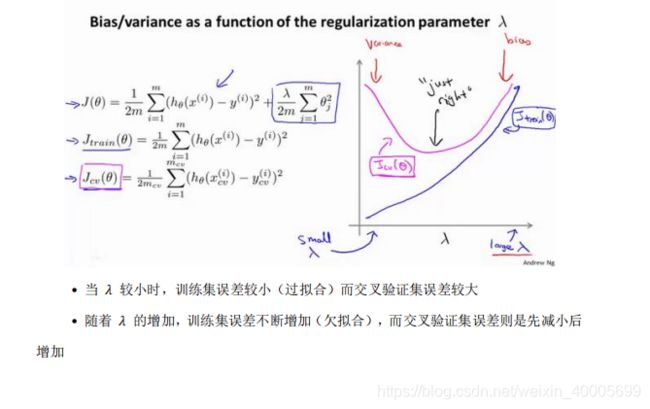
③正则化和偏差/方差
尝试改变想要测试的λ值
④学习曲线(改变m—训练集数据)
⑤结论
(增加多项式特征是指![]() )
)
高方差:获得更多训练实例;尝试减少特征数量;尝试增加正则化程度
高偏差:尝试获得更多特征;尝试增加多项式特征;尝试减少正则化程度
(6)构建学习算法
1. 从一个简单的能快速实现的算法开始,实现该算法并用交叉验证集数据测试这个算法2. 绘制学习曲线,决定是增加更多数据,或者添加更多特征,还是其他选择3. 进行误差分析:人工检查交叉验证集中我们算法中产生预测误差的实例,看看这些实例是否有某种系统化的趋势,并思考怎样能改进分类器4. 推荐使用量化数值评估
(7)偏斜类/skewed classes
类偏斜情况表现为我们的训练集中有非常多的同一种类的实例,只有很少或没有其他类的实例。
评估度量值——查准率(Precision)和查全率(Recall)
选择阀值的方法:![]() ,选择其中F值较高的
,选择其中F值较高的
三、支持向量机/SVM
(support vector machines)
简单点讲,SVM就是一种二类分类模型,他的基本模型是的定义在特征空间上的间隔最大的线性分类器,SVM的学习策略就是间隔最大化。
1.优化目标
2.大边界的直观理解
回顾 = 1/ ,因此:较大时,相当于 较小,可能会导致过拟合,高方差。较小时,相当于 较大,可能会导致低拟合,高偏差。
3.核函数
(Kernels)
![]()
常用核函数:线性核函数、高斯核函数
其余:多项式核函数、字符串核函数、卡方核函数、直方图交集核函数......
以上需要满足Mercer's定理
下面是一些普遍使用的准则:为特征数, 为训练样本数。(1) 如果相较于 而言, 要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。(2) 如果 较小,而且 大小中等,例如 在 1-1000 之间,而 在 10-10000 之间,使用高斯核函数的支持向量机。(3) 如果 较小,而 较大,例如 在 1-1000 之间,而 大于 50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
四、聚类
(Clustering)
1 无监督学习——聚类算法
2 K-均值算法(K-means)
K- 均值 是一个迭代算法,假设我们想要将数据聚类成 n 个组,其方法为 :①首先选择 个随机的点,称为 聚类中心 ( cluster centroids );②对于数据集中的每一个数据,按照距离 个中心点的距离,将其与距离最近的中心点关联起来,与同一个中心点关联的所有点聚成一类。③计算每一个组的平均值,将该组所关联的中心点移动到平均值的位置。④重复步骤 2-4 直至中心点不再变化。
3 优化目标
4 初始随机化
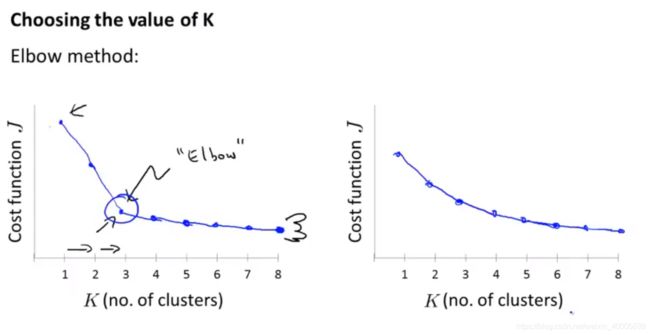
5 选取聚类数量
五、降维——PCA
(Dimensionality Reduction)
1 数据压缩/降维、数据可视化
2 主成分分析(PCA)
Principal Component Anayslis
PCA减少 维到 维:第一步是。我们需要计算出所有特征的均值,然后令。如果特征是在不同的数量级上,我们还需要将其除以标准差
。
第三步是计算协方差矩阵 的 特征向量 ( eigenvectors ) :奇异值分解
(可以理解为奇异值是特征值的推广,对长方形或者正方形但不满秩的矩阵,我们总可以求其奇异值。对于一般方阵两者不一定有联系。对于对称方阵,二者相等。)
选择主成分的数量
①我们可以先令 = 1,然后进行主要成分分析,获得![]() 和
和![]() ,然后计算比例是否小于1%。如果不是的话再令 = 2,如此类推,直到找到可以使得比例小于 1%的最小 值(原因是各个特征之间通常情况存在某种相关性)。
,然后计算比例是否小于1%。如果不是的话再令 = 2,如此类推,直到找到可以使得比例小于 1%的最小 值(原因是各个特征之间通常情况存在某种相关性)。
②
3 压缩重现
5 PCA应用
六、异常检测
(Anomaly Detection)
1 高斯分布/正态分布
2 利用高斯分布开发异常检测算法
①对于给定的数据集![]() ,我们要针对每一个特征计算
,我们要针对每一个特征计算 ![]() 和
和 ![]() 的估计值。
的估计值。
②给定新的一个训练实例,根据模型计算 (),当() < 时,为异常。
3 开发和评价一个异常检测系统
具体的评价方法如下:1. 根据测试集数据,我们估计特征的平均值和方差并构建 () 函数2. 对交叉检验集,我们尝试使用不同的 值作为阀值,并预测数据是否异常,根据 F1 值或者查准率与查全率的比例来选择3. 选出 后,针对测试集进行预测,计算异常检验系统的 1值,或者查准率与查全率之比。
4 异常检测与监督学习对比
|
异常检测
|
监督学习 |
| 非常少量的正向类(异常数据 = 1), 大量的负向类( = 0) | 同时有大量的正向类和负向类 |
|
许多不同种类的异常,非常难。根据非常少量的正向类数据来训练算法。
|
有足够多的正向类实例,足够用于训练算法,未来遇到的正向类实例可能与训练集中 的非常近似。 |
| 未来遇到的异常可能与已掌握的异常、非常的不同。 |
|
|
例如:欺诈行为检测 生产(例如飞机引擎) 检测数据中心的计算机运行状况
|
例如:邮件过滤器 天气预报 肿瘤分类 |
5 选择特征
6 多变量高斯分布
七、推荐系统
(Recommender Systems)
1 问题形式化
2 基于内容的推荐系统
3 协同过滤
④推行工作上的细节:均值归一化
八、大规模机器学习
如果我们有一个低方差的模型,增加数据集的规模可以帮助你获得更好的结果。我们应该怎样应对一个有 100 万条记录的训练集?以线性回归模型为例,每一次梯度下降迭代,我们都需要计算训练集的误差的平方和,如果我们的学习算法需要有 20 次迭代,这便已经是非常大的计算代价。首先应该做的事是去检查一个这么大规模的训练集是否真的必要,也许我们只用 1000个训练集也能获得较好的效果,我们可以绘制学习曲线来帮助判断
1 随机梯度下降法
2 小批量梯度下降
3 随机梯度下降收敛
4 在线学习
5 映射化简和数据并行
Map Reduce and Data Parallelism
吴恩达机器学习作业python实现 https://www.heywhale.com/mw/project/5da16a37037db3002d441810