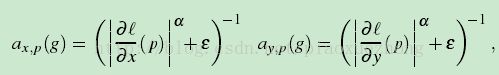加权最小二乘(wls)滤波算法原理及实现
加权最小二乘滤波WLS(weighted least squares)加上双边滤波,引导滤波是三种较为经典的边缘保持性滤波算法,该算法最早见于论文:《Edge-Preserving Decompositions for Multi-Scale Tone and Detail Manipulation》中,原作者项目主页:http://www.cs.huji.ac.il/~danix/epd/,本篇进行总结和测试。
加权最下二乘滤波原理:
作者提出该算法的初衷是,基于双边滤波的算法无法在多尺度上提取到很好的细节信息,并可能出现伪影。加权最小二乘滤波目的即是使得结果图像u 与原始图像 p经过平滑后尽量相似,但是在边缘部分尽量保持原状,用数学表达出来即为:
其中,ax,ay为权重系数。目标函数第一项(up−gp)2代表输入图像u和输出图像g越相似越好;第二项是正则项,通过最小化u的偏导,使得输出图像g越平滑越好。
上式可以改写为矩阵形式:
其中,Ax,Ay为以ax,ay为对角元素的对角矩阵,Dx,Dy为前向差分矩阵,DTx和DTy是后向差分算子,要使得(2)式去的最小值,u需满足如下:
其中,![]() ,作者去的平滑权重系数为:
,作者去的平滑权重系数为:
其中 l 表示log, ε一般取0.0001。式(3)求出μ为:
当所选区域连续是,平滑权重系数可以近似为:ax ≈ ay ≈ a,那么:
现在,式(5)未知变量就只剩下一个L了,L = DTxDx + DTyDy,可以看出,L为拉普拉斯齐次矩阵。更多内容可以参考《Efficient Preconditioning of Laplacian Matrices for Computer Graphics》,里面介绍了拉普拉斯矩阵的数学基础和应用。
加权最小二乘滤波实现:
原作者在项目主页中公布了源码,这里po一下,便于理解:
function OUT = wlsFilter(IN, lambda, alpha, L)
%WLSFILTER Edge-preserving smoothing based on the weighted least squares(WLS)
% optimization framework, as described in Farbman, Fattal, Lischinski, and
% Szeliski, "Edge-Preserving Decompositions for Multi-Scale Tone and Detail
% Manipulation", ACM Transactions on Graphics, 27(3), August 2008.
%
% Given an input image IN, we seek a new image OUT, which, on the one hand,
% is as close as possible to IN, and, at the same time, is as smooth as
% possible everywhere, except across significant gradients in L.
%
%
% Input arguments:
% ----------------
% IN Input image (2-D, double, N-by-M matrix).
%
% lambda Balances between the data term and the smoothness
% term. Increasing lambda will produce smoother images.
% Default value is 1.0
%
% alpha Gives a degree of control over the affinities by non-
% lineary scaling the gradients. Increasing alpha will
% result in sharper preserved edges. Default value: 1.2
%
% L Source image for the affinity matrix. Same dimensions
% as the input image IN. Default: log(IN)
%
%
% Example
% -------
% RGB = imread('peppers.png');
% I = double(rgb2gray(RGB));
% I = I./max(I(:));
% res = wlsFilter(I, 0.5);
% figure, imshow(I), figure, imshow(res)
% res = wlsFilter(I, 2, 2);
% figure, imshow(res)
if(~exist('L', 'var')), %如果参数不存在,所取默认值,下同
L = log(IN+eps);
end
if(~exist('alpha', 'var')),
alpha = 1.2;
end
if(~exist('lambda', 'var')),
lambda = 1;
end
smallNum = 0.0001;
[r,c] = size(IN);
k = r*c;
% Compute affinities between adjacent pixels based on gradients of L
dy = diff(L, 1, 1); %对L矩阵的第一维度上做差分
dy = -lambda./(abs(dy).^alpha + smallNum);
dy = padarray(dy, [1 0], 'post'); %在最后一行后面补一行0
dy = dy(:); %按列生成向量,就是Ay对角线上元素构成的矩阵,下同
dx = diff(L, 1, 2);
dx = -lambda./(abs(dx).^alpha + smallNum);
dx = padarray(dx, [0 1], 'post');
dx = dx(:);
% Construct a five-point spatially inhomogeneous Laplacian matrix
B(:,1) = dx;
B(:,2) = dy;
d = [-r,-1];
A = spdiags(B,d,k,k);
e = dx;
w = padarray(dx, r, 'pre'); w = w(1:end-r);
s = dy;
n = padarray(dy, 1, 'pre'); n = n(1:end-1);
D = 1-(e+w+s+n);
A = A + A' + spdiags(D, 0, k, k);
% Solve
OUT = A\IN(:);
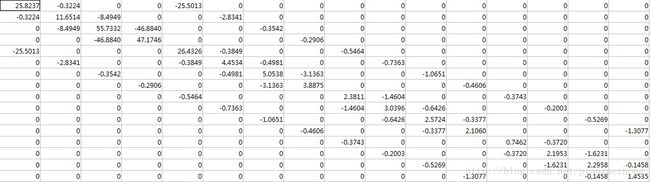
OUT = reshape(OUT, r, c);这里A+A′构造的是拉普拉斯非主对角线元素,D是主对角线元素。n,s,w,e是上(北)下(南)左(西)右(东)四个方位。 最终生成的一副拉普拉斯矩阵图:
图中每一行元素之和都为0。其中紧靠主对角线元素的两个对角线填充的是dy元素,比较远的对角线填充的是dx元素,这样拉普拉斯矩阵处理的就是二维图像了。
%% 加权最小二乘滤波测试函数
clc,close all,clear all;
RGB = imread('flower.png');
% if length(size(RGB))>2
% I = double(rgb2gray(RGB));
% else
% I=double(RGB);
% end
I=double(RGB);
res=I;
if length(size(RGB))>2
for i=1:3
I(:,:,i) = I(:,:,i)./max(I(:));
res(:,:,i) = wlsFilter(I(:,:,i));
end
end
figure,
subplot(211),imshow(I),title('原图');
subplot(212), imshow(res),title('wls-output');参考:
http://blog.csdn.net/bluecol/article/details/48576253
Edge-preserving decompositions for multi-scale tone and detail manipulation. ACM Transactions on Graphics
Efficient preconditioning of laplacian matrices for computer graphics[J]. ACM Transactions on Graphics