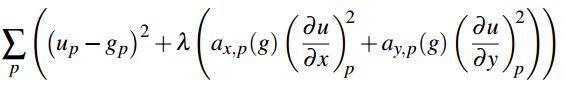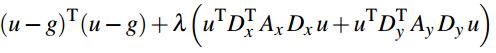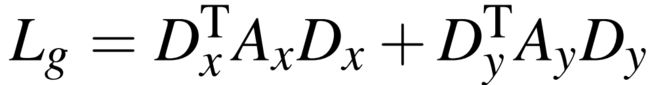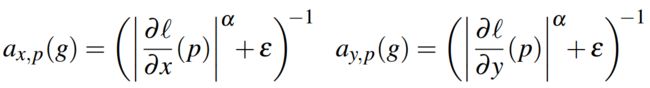加权最小二乘(WLS)图像滤波原理剖析及代码解读(并以人脸磨皮示例)
加权最小二乘滤波器是一种保边滤波器,其目标是是滤波结果尽可能接近原图,同时在梯度较小区域尽可能平滑,而强梯度的边缘部分尽可能保持。记原图为![]() ,待求解的滤波结果为
,待求解的滤波结果为![]() ,
,![]() 、
、![]() 分别为x和y方向梯度的权值矩阵,则损失函数
分别为x和y方向梯度的权值矩阵,则损失函数![]() 可表示为:
可表示为:
其中,![]() 为像素点坐标。
为像素点坐标。
其矩阵形式为:
其中,![]() 、
、![]() 为图像的向量表示。设图像大小为
为图像的向量表示。设图像大小为![]() ,令
,令![]() ,则其为
,则其为![]() 的列向量。
的列向量。![]() 、
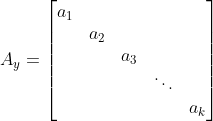
、![]() 为
为![]() 的对角权值矩阵,
的对角权值矩阵,![]() 、
、![]() 为 离散差分算子的矩阵表示。令
为 离散差分算子的矩阵表示。令![]() 导数为0,可得优化目标的解满足的方程:
导数为0,可得优化目标的解满足的方程:
其中,
这里权值应该是一个随着梯度增大而单调减的函数,这样给小梯度分配高权重就会迫使最优解在原来较平缓的地方变得更平缓。作者使用的权值函数如下:
很多人不明白差分算子的矩阵表示到底是怎么回事,这里就给大家简单介绍一下。以前向差分为例,若y方向为列方向、x方向为行方向。则严格意义的![]() 形如:
形如:
0值行对应每列的最后一个元素,因为不能拿下一列的第一个元素减去该元素作为该位置的前向差分。考虑到图像的行数一般很大,所以即便这样相减了(代表了将第一行与最后一行错位相减的梯度值也计入目标函数),对于整个求解的影响也可以忽略。为了表达的简洁性和构造方便起见,实际计算中![]() 是没有零值行的。当然啦,图像肯定不止两列,这里因为用编辑器写矩阵太麻烦了才没写完整。
是没有零值行的。当然啦,图像肯定不止两列,这里因为用编辑器写矩阵太麻烦了才没写完整。
则有:
![]() 与
与![]() 的形式类似,只是每行的-1和+1之间隔着
的形式类似,只是每行的-1和+1之间隔着![]() 个0,毕竟x方向上相邻两个元素的索引差值是
个0,毕竟x方向上相邻两个元素的索引差值是![]() 。相应的
。相应的![]() 、
、![]() 也都需要做类似调整。
也都需要做类似调整。
下面让我们看一下源代码:
function OUT = wlsFilter(IN, lambda, alpha, L)
%WLSFILTER Edge-preserving smoothing based on the weighted least squares(WLS)
% optimization framework, as described in Farbman, Fattal, Lischinski, and
% Szeliski, "Edge-Preserving Decompositions for Multi-Scale Tone and Detail
% Manipulation", ACM Transactions on Graphics, 27(3), August 2008.
%
% Given an input image IN, we seek a new image OUT, which, on the one hand,
% is as close as possible to IN, and, at the same time, is as smooth as
% possible everywhere, except across significant gradients in L.
%
%
% Input arguments:
% ----------------
% IN Input image (2-D, double, N-by-M matrix).
%
% lambda Balances between the data term and the smoothness
% term. Increasing lambda will produce smoother images.
% Default value is 1.0
%
% alpha Gives a degree of control over the affinities by non-
% lineary scaling the gradients. Increasing alpha will
% result in sharper preserved edges. Default value: 1.2
%
% L Source image for the affinity matrix. Same dimensions
% as the input image IN. Default: log(IN)
%
%
% Example
% -------
% RGB = imread('peppers.png');
% I = double(rgb2gray(RGB));
% I = I./max(I(:));
% res = wlsFilter(I, 0.5);
% figure, imshow(I), figure, imshow(res)
% res = wlsFilter(I, 2, 2);
% figure, imshow(res)
if(~exist('L', 'var')),
L = log(IN+eps);
end
if(~exist('alpha', 'var')),
alpha = 1.2;
end
if(~exist('lambda', 'var')),
lambda = 1;
end
smallNum = 0.0001;
[r,c] = size(IN);
k = r*c;
% Compute affinities between adjacent pixels based on gradients of L
dy = diff(L, 1, 1);
dy = -lambda./(abs(dy).^alpha + smallNum);
dy = padarray(dy, [1 0], 'post');
dy = dy(:);
dx = diff(L, 1, 2);
dx = -lambda./(abs(dx).^alpha + smallNum);
dx = padarray(dx, [0 1], 'post');
dx = dx(:);
% Construct a five-point spatially inhomogeneous Laplacian matrix
B(:,1) = dx;
B(:,2) = dy;
d = [-r,-1];
A = spdiags(B,d,k,k);
e = dx;
w = padarray(dx, r, 'pre'); w = w(1:end-r);
s = dy;
n = padarray(dy, 1, 'pre'); n = n(1:end-1);
D = 1-(e+w+s+n);
A = A + A' + spdiags(D, 0, k, k);
% Solve
OUT = A\IN(:);
OUT = reshape(OUT, r, c);其中,B(:,1)是编号为-r与r(主对角线编号为0,往左下方数编号分别为-1,-2,...-k-1,往右上方数编号分别为1,2,...k-1)的对角线上的元素,对应上面![]() 中的非主对角线。B(:,2)是编号为-1与1的次对角线上的元素,对应上面
中的非主对角线。B(:,2)是编号为-1与1的次对角线上的元素,对应上面![]() 中的次主对角线。
中的次主对角线。
-(e+w)就是![]() 主对角线上的元素,-(s+n)就是
主对角线上的元素,-(s+n)就是![]() 次对角线上的元素。五点对角阵的
次对角线上的元素。五点对角阵的![]() 就是这样构造的。
就是这样构造的。
至于WLS的用途嘛,WLS可广泛应用于图像去噪、HDR图像色调调制、图像细节增强、图像抽象等领域。详情参见论文原文或者https://blog.csdn.net/zhaoyin214/article/details/102714697。这里就不多做介绍了。
下面给出一个WLS滤波用于人脸磨皮的示例程序:
clear all;close all;clc;
img=imread('1.png');
ycc=rgb2ycbcr(img);
nimg=ycc(:,:,1);
lambda=0.1;
alpha=1.8;
diff = uint8(wlsFilter(double(nimg), lambda,alpha,double(nimg)/50));
fimg=ycbcr2rgb(cat(3,diff,ycc(:,:,2:3)));
figure,imshow(img);
figure,imshow(fimg);
figure,imshow(uint8((double(fimg)+double(img))/2)); %与原图加权叠加,保留自然感
imwrite(fimg,'res.jpg');原图:
滤波结果:
保留自然感的叠加结果:
需要说明的一点是,通过调节lambda、alpha值和用于计算权重矩阵![]() 、
、![]() 的权重引导图像(函数的第四个参数),我们可以控制得到滤波结果的缓变区域的平滑度和突变区域的锐利度。在合适的参数下,滤波本身所得结果就可以具备不错的自然感,这里是为了演示获得自然感的常用手段(即原图与平滑图像加权叠加)才这样处理的。
的权重引导图像(函数的第四个参数),我们可以控制得到滤波结果的缓变区域的平滑度和突变区域的锐利度。在合适的参数下,滤波本身所得结果就可以具备不错的自然感,这里是为了演示获得自然感的常用手段(即原图与平滑图像加权叠加)才这样处理的。