最优化笔记

最优化技术

一维搜索技术

一维无约束优化问题：min f(x)

步骤：

• 确定初始的搜索区间[a,b]，在此区间是单峰区间，函数呈现”大-小-大“变化趋势
• 在搜索区间找到极小值点（试探法：黄金分割，二分，Fibonacci 插值法：牛顿插值，割线法）

进退法

• a0,h>0，令a1=a0，a2=a1+h，f1,f2
• 若f2
• 令a3=a2+h,f3=f(a3)
• 若f3>f2，结束运算,[a,b]=[a1,a3]
• 否则，加大步长继续搜索。 h=2*h，a1=a2，a2=a3，a3=a2+h

如果f2>f1，后退运算

• h=-h，a1,a2=a2,a1,a3=a2+h

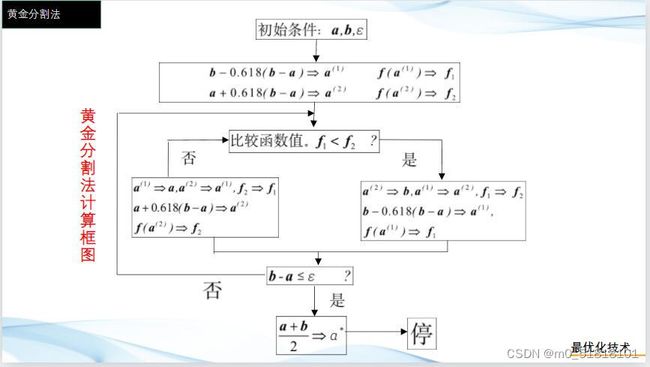
黄金分割法

步骤：

• 置初始搜索区间[a,b]，并置精度要求$ϵ$,并计算左右试探点
  • a1=a+0.318(b-a); a2=a+0.618(b-a)
• 比较f1和f2的大小
  • 若f1>f2,极小点在[a1,b],a=a1,a1=a2,a2=a+0.618(b-a);
  • 若f1<=f2，极小点在[a,a2]，b=a2,a2=a1,a1=a+0.382(b-a)
• 当缩短的区间长度小于精度$ϵ$,极小点=(a+b)/2

Fibonacci法

• 与黄金分割法一致，设初始区间[a,b]有唯一的极小值点，规定一共计算n次

$$\begin{gathered} s.t.F_N>=(b-a)/ϵ \\ 取试探点x_1=\frac{F_{n-2}}{F_n}(b-a)+a \\ {x}_2=\frac{F_{n-1}}{F_n}(b-a)+a \end{gathered}$$

• 如果$f_1<=f_2$ 最小值在[a,$x_2$]，b=$x_2{x}_2=x_1$ $x_1=a+\frac{F_{n-2-k}}{F_{n-k}}k=1\dots n-2$
• 如果$f_1>f_2$,最小值在[$x_1$,b], a=x1,x1=x2, $x_2=a+\frac{F_{n-1-k}}{F_{n-k}}(b-a)$
• 如果k=n-2

二分法

基本原理：

• 取具有极小点的单峰函数的搜索区间[a,b]的坐标中点$\frac{a+b}{2}$作为计算点，计算目标函数在该点处的导数
• 利用函数在极小点的导数为0，在其左侧为负，在其右侧为正的原理
  • 若 $ f’(\frac{a+b}{2}) $ < 0 , 则搜索区间为 $[\frac{a+b}{2},b]$
  • 若 $f^{\prime }(\frac{a+b}{2})$ > 0，则搜索区间为 $[a,\frac{a+b}{2}]$
• 逐次迭代下去，直到搜索区间收敛到局部极小点。

计算步骤：

给定 $a,b,{\epsilon }_1,{\epsilon }_2$

• 计算 ${\alpha }_k=\frac{a+b}{2},若|b-a|<={\epsilon }_1$,停止迭代，取得结果为${\alpha }_k$，停止迭代，否则下一步。
• 计算$f^{\prime }({\alpha }_k),若f^{\prime }({\alpha }_k)=0或者f^{\prime }({\alpha }_k)<={\epsilon }_2$,停止迭代，否则：
  • 若$f’(\alpha_k) < 0 $,则取[$\alpha_k$,b] 转（1）
  • 若$f^{\prime }({\alpha }_k)>0$,则取[$a,{\alpha }_k$] 转（1）

牛顿插值法

梯度下降法

参考链接：

优化思想：用当前位置的负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，最速下降法越接近目标值，步长越小，前进越慢

梯度的含义：

• 在单变量的函数当中，梯度其实就是函数的微分，代表着函数在某个给定点的切率
• 在多变量的函数当中，梯度就是一个方向，向量有方向，梯度的方向指出了函数在给定点上升最快的方向

$${\theta }^1={\theta }^0-\alpha \nabla J(\theta )$$

$\alpha$称之为学习率或者步长，不能太大或太小

场景分析：线性回归
用梯度下降法拟合出一条直线

首先需要定义一个代价函数，这里选用均方误差代价函数（平均误差函数）
$$J(\theta )=\frac{1}{2m}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
在此公式当中

• m是数据集中数据点的个数，也就是样本数
• 1/2是一个常量，这样是为了在求梯度的时候，二次方求导下来的2就和1/2抵消了
• y是数据集中每个点真实的y坐标的值
• h是我们的预测函数，直线方程$h_{\theta }(x^{(i)})={\theta }_0+{\theta }_1{x}_1^{(i)}$

共轭梯度

补充定义：

• 正定矩阵：M是n阶方阵，如果对于任何非零向量z,都有$z^{T}Mz$>0,M为正定矩阵

共轭方向指的是若干个方向矢量组成的方向组，各方向有着相同的性质，它们之间存在特定的关系
$$\begin{gathered} x^{(1)}是在某个等值面上的一点s^{(1)}是R^n中的一个方向 \\ {x}^{(0)}沿着s^{(1)}以最优步长搜索得到点x^{(1)} \\ 则S^{(1)}是点x^{(1)}所在的等值面的切向量 \\ 法向量为▽f(x^{(1)})=A(x^{(1)}-x) \\ {S}^{(1)T}▽f(x^{(1)})=0 \\ {S}^{(2)}=x-x^{(1)} \\ {s}^{(1)T}A{s}^{(2)}=0 \\ 等值面上一点处的切向量与由这个点指向极小点的向量关于A共轭 \end{gathered}$$

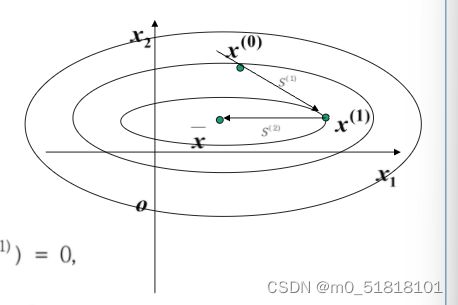
同心椭圆簇的几何性质：任意做两条平行线，与椭圆组中的两椭圆切于点 x(1)，x(2) 。该两点必通过椭圆的中心；或者说，过椭圆中心做任意直线与任意两个椭圆相交，通过交点作椭圆切线必互相平行

共轭方向法对于n阶对称正定矩阵A，至多需要n次迭代就可以得到最优解

如何选取一组共轭方向？

利用已知迭代点处的梯度方向构造一组共轭方向，并且沿此方向进行搜索，求出函数的极小点

（1）搜索步长的确定

已知迭代点$x^{(k)}$和搜索方向$d^{(k)}$,利用一维搜索确定最优步长${\lambda }_k$
$$\begin{gathered} 求解minf(x^{(k)}+\lambda d^{(k)}) \\ \phi (\lambda )=f(x^{(k)}+\lambda d^{(k)}) \\ 令\phi (\lambda {)}^{\prime }=▽f(x^{(k)}+\lambda d^{(k)}{)}^T{d}^{(k)}=0 \\ 已知▽f(x)=Ax+b \\ 即有|A(x^{(k)}+\lambda d^{(k)})+b{|}^T{d}^{(k)}=0 \\ 令g_k=▽f(x^{(k)})=A{x}^{(k)}+b,则有 \\ |g_k+\lambda A{d}^{(k)}{|}^T{d}^{(k)}=0 \\ 解得{\lambda }_k=-\frac{g_k^T{d}^{(k)}}{d^{(k{)}^T}A{d}^{(k)}} \end{gathered}$$

（2）搜索方向的确定

• 任意取得初始点$x^{(1)}$,第一个搜索方向取为 $d^{(1)}=-▽f(x^{(1)})$;
• 设已求得点$x^{(k+1)},若▽f(x^{(k+1)})不等于0，令$ $g_{k+1}=▽f(x^{(k+1)})$

$$\begin{gathered} 则下一个搜索方向按照如下方式确定： \\ 令d^{(k+1)}=-g_{k+1}+{\beta }_k{d}^{(k)} \\ 其中d^{k+1}和d^k关于A共轭 \\ {d}^{(k{)}^T}A{d}^{(k+1)}=0 \\ 解得{\beta }_k=\frac{d^{(k{)}^T}A{g}_{k+1}}{d^{(k{)}^T}A{d}^{(k)}} \end{gathered}$$

共轭梯度算法性质

对于正定二次函数 $f(x)=\frac{1}{2}{x}^{T}Ax+b^T+c$,FR算法在n次以内搜索终止。

• 搜索方向 $d^{(1)},d^{(2)},\dots d^{(m)}$关于A共轭。

共轭梯度算法步骤(正定二次函数)

• 任取初始点$x^{(1)}$,精度要求$\epsilon$,令k=1

• 令$g_1=▽f(x^{(1)})$,如果||$g_1$||<$\epsilon$,停止，$x^{(1)}$为所求的极小点，否则，令$d^{(1)}=-g_1$，利用公式（3）计算${\lambda }_1,令x_2=x_1+{\lambda }_1{d}^{(1)}$

• 计算$g_{k+1},如果g_{k+1}小于精度，停止$

  否则， 令$d^{(k+1)}=-g_{k+1}+{\beta }_k{d}^{(k)}$,其中${\beta }_k$用${\beta }_i=\frac{||g_{i+1}|{|}^2}{||g_i|{|}^2}$ k=k+1

• 利用公式(3)计算${\lambda }_k$, 算出$x_{k+1}$

对于一般函数，搜索步长${\lambda }_i$需要一维搜索确定

注意：PPT上求解步长公式推导使用了正定二次函数性质，但方向推导没有，所以方向公式适用于一般函数。

算法在有限步迭代后不一定能满足停止条件：以n次迭代为一轮，每次完成一维搜索后，如果还没有求得极小值，则以上一轮的最后一个迭代点作为新的初始点，取最速下降方向为第一个搜索方向，开始下一轮搜索

线性规划

基本概念

在一组线性约束条件下，求解目标函数的最优解

线性规划标准形式：

• 目标函数求最大值，注意一维搜索是寻找最小值
• 所有的约束条件均由等式表示
• 每个约束条件右端常数常为非负值
• 所有决策变量为非负值

若不满足，改造方法如下：

• 若目标函数求最小值，添加负号改为求最大值
• 约束条件中，某些常数项bi为负数，则在约束条件两边乘以负号。
• 约束条件为不等式：
  • <= 左边加上非负数
  • >= 左边减去非负数
• 若某一变量 $x_j<=0,则令x_j^{\prime }=x_j$
• 若某一变量无符号限制，则需要添加两个非负变量吗$V_k,U_k,令x_k=V_k-U_k$

设线性规划约束方程组的系数矩阵$A_{m\ast n}$的秩为m，则A中某m列组成的任一个m阶可逆矩B称之为该线性规划问题的一个基矩阵。

当Ax=b式中A确定一个基B后，与基向量$p_k$相对于的决策变量$x_k$称为关于基B的一个基变量。

设 $B=p_{k1},p_{k2},\dots ,p_{km}$ 是A中的一个基，对应的基变量为$x_{k1},x_{k2},x_{k3},\dots ,x_{km}$,我们称非基变量取值均为0且满足约束条件的一个解x为基B的一个基本解。

三条重要定理：

• 若线性规划问题存在可行解，则该问题的可行域是凸集。
• 线性规划问题的基本可行解X对应可行域（凸集）的顶点
• 若问题存在最优解，一定存在一个基本可行解是最优解。

单纯形法

迭代原理：

1. 选择初始基，确定初始基本可行解。
2. 判断当前解是否是最优解
   1. 将基变量用非基变量表示，并用非基变量表示目标函数
   2. 当目标函数中所有非基变量系数小于等于0时，才是最优解。若某一个非基变量等于0，由无穷多个最优解
3. 解的改进，找出目标函数中贡献最大的非基变量，让非基变量的取值从0变为整数，即将x2从非基变量转换为基变量，称之为进基变量。再从原来基变量中选择一个离开。
4. 用非基变量（此时还未替换）去表示基变量（马上有人要退出了），让进基变量从0开始增加，使得有一个基变量减少到0就停止，此时变为0的基变量称之为离基变量。

最优解判定定理

对于求最大目标函数的问题中，对于某个可行的基本可行解，所有的检验数$\sigma <=0$，这个基本可行解才是最优解

• 当非基变量的检验数都小于0，存在唯一最优解
• 非基变量的检验数存在等于0，则有无穷多最优解
• 存在某非基变量的检验数大于0，但该变量对应的所有系数都小于等于0，是无界解。
• 添加人工变量之后，当所有的非基变量的检验数都小于等于0，而基变量中有人工变量时，则问题无可行解。

单纯形表值得注意的地方： 找出基变量找检验数最大所对应的变量，找离基变量时找对应系数最小的变量。

为了避免退化问题造成反复循环，在选出基和入基变量的时候：

• 在所有检验数大于0且相同的非基变量中，选一个下标最小的作为入基变量
• 在存在两个和两个以上相同比值时，选一个下标最小的基变量为出基变量。

动态规划

引例

任务选择问题

opt(i) 表示完成前 i 个任务的最优解

状态转移方程：
$$\begin{gathered} opt[i]=max\{v(i)+opt[prev(i)],opt(i-1)\} \\ 终止条件：opt[0]=0 \end{gathered}$$

不相邻数选择

opt[i] 表示选择前i个数的最大和

状态转移方程：
$$\begin{gathered} opt[i]=max\{a[i]+opt[i-2],opt[i-1]\} \\ 出口：opt[0]=a[0],opt[1]=max\{a[0],a[1]\} \end{gathered}$$

动态规划问题的特征

最优子结构

问题的最优解包含了其他子问题的最优解

重叠子问题

投资分配问题

将a万元分给n个工厂，xi为分给第i个工厂资金，gi(xi)为第i个工厂得到资金后提供的利润值

令 fk(x)表示将x万元资金分给前k个工厂所得到的最大利润， gk(y)表示将y万元资金分给第k个工厂所获得的利润。

状态转移方程：
$$f1(x)=g1(x)f_{k}k(x)=max\{f_{k-1}(x-y)+gk(y)\},其中0<=y<=x$$

背包问题

有一个徒步旅行者，其可携带物品重量的限度为a 公斤，设有n 种物品可供他选择装入包中。已知每种物品的重量及使用价值（作用），问此人应如何选择携带的物品（各几件），使所起作用（使用价值）最大？

令 fk(y) 表示只带前k种物品，重量不超过y所获得的最大利润。 求解 fn(a).

状态转移方程
$$\begin{gathered} f_k(y)=max\{f_{k-1}(y-a_k{x}_k)+c_k{x}_k\},其中0<=x_k<=\frac{y}{a_k} \\ 当k=1，f_1(y)=c_1(\frac{y_1}{a_1}) \end{gathered}$$

排序问题

状态变量 （X,t）

X:在机床A上等待加工的工件集合

x:不属于X的在A上最后加工完的工件

t:在A上加工完x的时刻算起到B上加工完x所需的时间

指标最优值函数：

f(X,t) : 由状态(X,t)出发，对未加工的工件采取最优加工顺序后，将X所有工件加工所需时间。

f(X,t,i):由状态(X,t)出发，在A上加工i，然后对未加工工件采取最优加工顺序后，将X中所有工件加工完所需时间

f(X,t,i,j):由状态(X,t)出发，在A上加工工件i,j，然后再对未加工工件采取最优加工顺序后，将X中所有工件加工完所需要的时间。

状态转移方程 ： (X,t) ----> (X-i,$z_i(t)$) Zi(t)表示从 状态(X,t)出发，从A上加工完i工件时刻算起到B上加工完i工件所用的时间。
$$f(X,t,i)=\{\begin{array}{c}{a}_i+f(X/i,t-a_i+b_i)t\ge a_i\\ a_i+f(x/i,b_i)t\le a_i\end{array}$$
是不是看不懂？，我也是哈哈，然而看到下面你就会了，上面建议跳过，非常坑人

加工总周期 ： $ T = \sum t_{Ai} + t_{Bmin}$

n $\times$ 3排序问题

将 $n\times 3$排序问题转换为$n \times 2 $排序问题。

just don’t bi bi. show me the example

加工总周期： $T=\sum t_{Ai}+t_{Bmin}+t_{Cmin}$

遗传算法

遗传算法是一种通过模拟自然进化 过程搜索最优解的方法

轮盘赌选择法

参考文档：https://blog.csdn.net/weixin_39068956/article/details/105121469

目的：有若干个备选方案，而且每个方案都有自己的潜力分值，但是在选择的时候并不完全按照分值的高低来选，而是有一定的概率接受，分值高的接受概率高，分值较低接受的概率也低。

思想

各个个体的被选择概率和其适应度值成比例，适应度越大，被选中的概率也就越大。

每个部分被选中的概率与其适应度成比例。设一部分x(i)的适应度表示为f(xi),被选中的概率为p(xi),累计概率为q(xi)，对应的计算公式如下：
$$\begin{gathered} P(x_i)=\frac{f(x_i)}{{\sum }_{j=1}^{N}fj} \\ q(xi)=\sum _{j=1}^{i}p(x_j) \end{gathered}$$

过程

• 计算每个个体被选中的概率
• 计算每个部分的累计概率
• 随机生成一个数组m，数组中的元素取值范围在0到1之间，并将其按照从大到小的方式进行排序，若累计概率q(xi)大于数组中的元素，则个体x(i)被选中，若小于m(i)，则比较下一个个体，直至选出一个个体为止。

交叉算子

参考文档：https://blog.csdn.net/u010743448/article/details/108445588

• 一点交叉
• 二点交叉
• 多点交叉
• 部分匹配交叉

部分匹配交叉（PMX）

参考文档：https://blog.csdn.net/Juuunn/article/details/108948237

保证了每个染色体中的基因仅仅出现一次，常用于旅行商和其他排序问题

• 随机选择一对染色体中几个基因的起始位置
• 交换这两组基因的位置
• 做冲突检测，根据交换的两组基因建立一个映射关系，所有冲突的基因都会经过映射，保证下一代基因无冲突

顺序交叉（OX）

• 与PMX相同，随机选择一对染色体（父代）中几个基因起止位置
• 生成一个子代，并保证子代被选中的基因的位置与父代相同
• 首先找出第一步选中的基因在另一个父代中的位置，再将其余基因按照顺序放入上一步生成的子代当中

基于位置的交叉（PBX）

在两个父代染色体中随机选择几个位置，位置可以不连续，将父代染色体1这些位置上的基因复制到子代1相同位置上，再在父代染色体2上将子代1中缺少的基因按照顺序填入。另一个子代以类似方式得到。PBX与OX的不同在于选取的位置可以不连续。

遗传算法基本思想：在求解问题时从多个解开始，然后通过一定的法则进行逐步迭代以产生新的解

基本流程

• 通过随机的方式产生若干个确定长度编码的初始群体
• 通过适应度函数对每个个体进行评价，选择适应度高的个体参与遗传操作，适应度低的被淘汰
• 经过遗传操作（复制，交叉，变异）的个体形成新的一代种群，直到满足停机准则。
• 然后将后代表现好的个体做为遗传算法的执行结果。

人工神经网络（ANN）

参考博客：https://www.cnblogs.com/mantch/p/11298290.html#:~:text=%E6%AD%A3%E5%90%91%E4%BC%A0%E6%92%AD,%28forward-propagation%29%E6%98%AF%E6%8C%87%E5%AF%B9%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E6%B2%BF%E7%9D%80%E4%BB%8E%E8%BE%93%E5%85%A5%E5%B1%82%E5%88%B0%E8%BE%93%E5%87%BA%E5%B1%82%E7%9A%84%E9%A1%BA%E5%BA%8F%EF%BC%8C%E4%BE%9D%E6%AC%A1%E8%AE%A1%E7%AE%97%E5%B9%B6%E5%AD%98%E5%82%A8%E6%A8%A1%E5%9E%8B%E7%9A%84%E4%B8%AD%E9%97%B4%E5%8F%98%E9%87%8F%20%28%E5%8C%85%E6%8B%AC%E8%BE%93%E5%87%BA%29%E3%80%82

概述

• 外部刺激通过神经末梢，转换为电信号，转导到神经细胞（神经元）
• 无数神经元构成神经中枢
• 神经中枢综合各种信号，对外部刺激做出反应
• 人体根据神经中枢的指令，对外部的刺激做出反应。

激活函数

功能：判断从多个神经元传递过来的信号之和是否超过阈值，不超过不做出任何反应

实例：

单位阶跃函数

输入小于等于0时，输出0；当输出大于0，输出1；

Sigmoid型函数

$$\sigma (x)=\frac{1}{1+exp(-x)}$$

Tanh函数

$$tanh(x)=\frac{exp(x)-exp(-x)}{exp(x)+exp(-x)}$$

ReLU函数（常用）

$$ReLU(x)=max(0,x)$$

交叉熵损失函数

$$L_i=-log(\frac{e^{S_{yi}}}{\sum j{e}^{sj}})$$

注意：神经网络的激活函数必须使用非线性函数

原因：如果使用线性函数，那么不管如何加深层数，总是存在与之等效的”无隐藏层神经网络“。

人工神经网络

• 输入层：网络输入层的每个神经元代表了一个特征

• 输出层：输出层个数代表分类标签的个数（在做二分类的时候，如果采用sigmoid分类器，输出层的神经元为1个；如果采用softmax分类器，输出层神经元个数为2个）

神经网络主要用于解决监督学习中的分类问题，主要通过带标记的数据集训练神经网络，不断调节权重，使得误差最小后。利用训练好的权重对数据进行分类。

1+exp(-x)}
$$

Tanh函数

$$tanh(x)=\frac{exp(x)-exp(-x)}{exp(x)+exp(-x)}$$

ReLU函数（常用）

$$ReLU(x)=max(0,x)$$

交叉熵损失函数

$$L_i=-log(\frac{e^{S_{yi}}}{\sum j{e}^{sj}})$$

注意：神经网络的激活函数必须使用非线性函数

原因：如果使用线性函数，那么不管如何加深层数，总是存在与之等效的”无隐藏层神经网络“。

人工神经网络

• 输入层：网络输入层的每个神经元代表了一个特征

• 输出层：输出层个数代表分类标签的个数（在做二分类的时候，如果采用sigmoid分类器，输出层的神经元为1个；如果采用softmax分类器，输出层神经元个数为2个）

神经网络主要用于解决监督学习中的分类问题，主要通过带标记的数据集训练神经网络，不断调节权重，使得误差最小后。利用训练好的权重对数据进行分类。