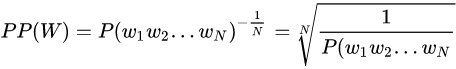NLP 文本分类实战

语言模型

语言模型用来判断：一句话从语法上是否通顺。通俗的讲就是判断一句话是不是人说的话的模型，即能够判断出$p(Iwanttolearnnlp)>p(Iwanttonlplearn)$

通常情况下一个句子由若干词或者字组成，若句子用 $s$ 表示，组成句子的词用 $w$ 表示，可记做 $w_1,w_2,w_3,w_4,...,w_n$ ，如下所示：

• $p(s)=p(w_1,w_2,w_3,w_4,...,w_n)$

• $p(我要学习NLP)=p(我,要,学习,NLP)$

如何计算一个句子出现的概率 ？在此之前需要了解一个 Chain Rule 的数理统计的知识，如下：

• $p(A,B,C,D)=p(A)\cdot p(B|A)\cdot p(C|A,B)\cdot p(D|A,B,C)$

  • $p(A,B)=p(A)\cdot p(B|A)$
  • $p(A,B,C)=p(A,B)\cdot p(C|A,B)$

• $p(w_1,w_2,w_3,w_4,...,w_n)=p(w_1)\cdot p(w_2|w_1)....p(w_n|w_1{w}_2{w}_3{w}_4...w_{n-1})$

那么，对于句子“ 我要学习NLP” 来说，计算其概率可采用 Chain Rule 的规则方法。

• $p(我要学习NLP)=p(我,要,学习,NLP)$

• $p(我,要,学习,NLP)=p(我)\cdot p(要|我)....p(NLP|我，要，学习)$

然而概率的条件越多，比如：$p(NLP|我，要，学习)$，符合概率的情况就越小。假如“我”出现的概率是0.0001，“要”出现的概率0.0001，“学习”出现的概率更小的话，一直累乘下去“NLP”出现的概率会越来越小。为了解决该问题，需要引入了 N-gram 模型来解决这个问题，N-gram 模型引入了马尔科夫假设（markov assumption），即当前词出现的概率只与其前 n-1 个词有关。

markov assumption

一个马尔科夫过程是状态间的转移仅依赖于前 $n$ 个状态的过程。这个过程被称之为 $n$ 阶马尔科夫模型。最简单的马尔科夫过程是一阶模型，它的状态选择仅与前一个状态有关。举个例子：

• 假设：当前词出现的概率与其他单词无关，Unigram model。不考虑单词之间的顺序
  • $p(NLP|我，要，学习)\approx p(NLP)$
• 假设：当前词出现的概率与距离最近的单词有关，Bigram model
• $p(NLP|学习)\approx p(NLP)$
• 假设：当前词出现的概率与前两个单词有关, Trigram model
  • $p(NLP|要，学习)\approx p(NLP)$
• 假设：当前词出现的概率只与其前 n-1 个词有关, N-gram model

Unigram model

$p(w_1,w_2,w_3,w_4,...,w_n)=p(w_1)...p(w_n)={\prod }_{i=1}^{n}p(w_i)$

Bigram model

$p(w_1,w_2,w_3,w_4,...,w_n)=p(w_1)\cdot p(w_2|w_1)...p(w_n|w_{n-1})=p(w_1){\prod }_{i=2}^{n}p(w_i|w_{i-1})$

Trigram model

$p(w_1,w_2,w_3,w_4,...,w_n)=p(w_1)\cdot p(w_2|w_1)\cdot p(w_3|w_1{w}_2)...p(w_n|w_1...w_{n-1})=p(w_1)p(w_2|w_1){\prod }_{i=3}^{n}p(w_i|w_{i-2}{w}_{i-1})$

在实践中用的最多的是 bigram 和 trigram。

例子

• $p(是|今天)=0.01$
• $p(今天)=0.002$
• $p(周日|是)=0.001$
• $p(周日|今天)=0.0001$
• $p(周日)=0.02$
• $p(是|周日)=0.0002$

比较：今天是周日 VS 今天周日是，采用 Bigram model

• $p(今天，是，周日)=p(今天)\cdot p(是|今天)\cdot p(周日|是)=0.002\ast 0.01\ast 0.0001=x$

• $p(今天,周日,是)=p(今天)\cdot p(周日|今天)\cdot p(是|周日)=0.002\ast 0.0001\ast 0.0002=y$

通过比较 $x$ 和 $y$ 的大小来得知那句话更符合语法。

评估语言模型的好坏

训练出来的语言模型，怎么评价模型的好坏？

理想情况下：

1. 假设有两个语言模型 A，B
2. 选定一个特定的任务比如拼写纠错
3. 把两个模型A，B都应用在此任务中
4. 最后比较准确率，从而判断A，B的表现

然而特定任务成本太高，有没有更简单的评估方法，不需要在特定的任务中验证，而困惑度（perplexity）便是一个衡量语言模型好坏的指标。

给定语料库下，更好的语言模型应该给更通顺的句子更高的概率，比如句子：天要下 _ 了。更好的语言语言模型 $p(雨｜天)$ 的概率应该更大。因为天要下雨了是非常符合逻辑的，当出现 “ 天要下 ” 这三个字，接下来是 “雨” 字的可能性更大。如果比较两个语言模型，那个语言模型 $p(雨｜天)$ 的概率更高，说明哪个语言模型更好。

Perplexity

困惑度与测试集上的句子概率相关，其基本思想是：给测试集的句子赋予较高概率值的语言模型较好,当语言模型训练完之后，测试集中的句子都是正常的句子，那么训练好的模型就是在测试集上的概率越高越好[1]，公式如下：

这里想补充一下参考资料里没有强调的一些点[2]:

1. 根号内是句子概率的倒数，所以显然 句子越好（概率大），困惑度越小，也就是模型对句子越不困惑。 这样我们也就理解了这个指标的名字。
2. 开N次根号（N为句子长度）意味着几何平均数（把句子概率拆成字符概率的连乘）

• 需要平均的原因是，因为每个字符的概率必然小于1，所以越长的句子的概率在连乘的情况下必然越小，所以为了对长短句公平，需要平均一下

• 是几何平均的原因，是因为其的特点是，如果有其中的一个概率是很小的，那么最终的结果就不可能很大，从而要求好的句子的每个字符都要有基本让人满意的概率

神经网络中的困惑度常常不是直接使用句子概率来计算的，而常常使用如下形式：

$perplexity=2^{-(x)},x:averageloglikehood$

例如：由 $w_1,w_2,w_3,w_4,w_5$ 组成的句子，如果采用 Bigram model 的 markov assumption，则 perplexity 的求解方式为：

$$\begin{gathered} P_{LM}(w_1,w_2,w_3,w_4,w_5) \\ =\frac{log{P}_{LM}(w_1)+log{P}_{LM}(w_2|w_1)+log{P}_{LM}(w_3|w_2)+log{P}_{LM}(w_4|w_3)+log{P}_{LM}(w_5|w_4)}{5}=x \end{gathered}$$
如果 $x$ 越大说明句子出现的概率越大，则 $perplexity=2^{-(x)}$ 越小，说明模型就越好。

Laplace Smoothing

Laplace Smoothing 解决零概率问题，就是在计算实例的概率时，如果某个量 $x$，在观察样本库（训练集）中没有出现过，会导致整个实例的概率结果是 0。在文本分类的问题中，当一个词语没有在训练样本中出现，该词语概率为 0，使用连乘计算文本出现概率时也为 0。这是不合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是 0。

举个例子：两句话，其中一句话明明更加通顺，但是语料库中没出现过它其中的一个词，所以它的概率就会为 0。这是不合理的。

Add-one Smoothing （Laplace Smoothing）

$P_{MLE}(w_i|w_{i-1})=\frac{c(w_{i-1},w_i)}{c(w_{i-1})}$

$P_{ADD-1}(w_i|w_{i-1})=\frac{c(w_{i-1},w_i)+1}{c(w_{i-1})+v}v是词库的大小$

例子

语料库：今天 上午 的 天气 很好 我 很 想 出去 运动 但 今天 上午 有 课程 没 办法 啊

$P_{MLE}(没有|上午)=\frac{0}{2}=0$

$P_{ADD-1}(没有|上午)=\frac{0+1}{2+v}=\frac{1}{2+18}=\frac{1}{20}$

Add-K Smoothing （Laplace Smoothing）

$P_{ADD-k}(w_i|w_{i-1})=\frac{c(w_{i-1},w_i)+k}{c(w_{i-1})+kv}v是词库的大小$

语言模型在拼写纠错中的应用

Spell Correction

目的如下，用户输入不对的词，可以进行纠正。

用户输入（input）	纠正输入（correction）
天起	天气
theris	theirs
机器学系	机器学习

find the words with smallest edit distance

其中一个纠正思路如下：

用户输入	候选	编辑距离
	there	1
	their	1
therr	thesis	3
	theirs	2
	the	2

其中一个方法是，输入 therr ，循环整个词库，计算词库中的词和输入词的编辑距离。然后对编辑距离进行排序就可以得到一个候选集，紧接着再根据哪个词更符合上下文等判断，来选出最佳的词。

alternative way

之前的方法：用户输入 -> 从词典中寻找编辑距离最小的 -> 返回 （需要遍历整个词库，$o（｜v｜）$为时间复杂度）

现在的方法：用户输入 -> 生成编辑距离为1，2的字符串 -> 过滤 -> 返回

如何过滤？

用户输入 -> 生成编辑距离为1，2的字符串作为候选词 -> 过滤 -> 返回

appl -> app， apple， apply -> 判断 appl 替换成候选词中哪个词更妥当 -> 返回

如何选择候选词？

假设 $w$ 是错误的单词，我们想把它改成正确的形式（ 记为 $c$ ）。一个单词错误的情况下，把它改造成另外一个词，我们希望下方的条件概率越大越好。

$$\begin{gathered} C=argmaxP（c|w） \\ =argmax\frac{P（w|c）P（c）}{P（w）} \\ =argmaxP（w|c）P（c）,cϵcandidates \end{gathered}$$

公式用到了贝叶斯定理，更多详细的描述可以移步查看文章：https://zhuanlan.zhihu.com/p/37768413

$P（w|c）$： $P（w|c）$ 是 $w$ 和 $c$ 相关的 score，如何得到这个 socre，有很多手段：

• 可以使用 edit distance 来评估：
  • 比如：edit distance = 1 时，score = 0.8
  • 比如：edit distance = 2 时，score = 0.2
• 可以使用 collected data 来评估：
  • $P（w|c）$ 当用户拼写 $c$ 的时候有多少概率把它拼错为 $w$ ，比如：
    • Apple ( 出现 12 次) -> appl ( 拼错 9 次) , Apple -> app ( 出现 2 次) , Apple -> appla ( 出现 1 次)
    • 那么拼错成 appl，app，appla 的概率分别为：9/12，1/6，1/12

$P（c）$ ：而 $P（c）$ 更像是语言模型：

比如有一个句子，这个句子是：I eat an appl ，it is a fruit. 其中 appl 是错误的词，我们需要把它替换成正确的，此时候选集有 apple，app。这时候可以使用语言模型来判断哪个词是更好的。

比如，使用 Bigram model：

I eat an ( apple ) it is a fruit

-> $P(apple|eat,an)P(it|an,apple)P(is|apple,it)P(a|it,is)$

I eat an ( app) it is a fruit

-> $P(app|eat,an)P(it|an,app)P(is|app,it)P(a|it,is)$

比较两个概率即可。

预处理

过滤词

在进行文本处理的时候，我们通常先把停用词、出现频率很低的词汇过滤掉。

• 停用词：的，地，is，the 等

分词算法

• jieba分词
• SnowNLP
• LTP
• HanNLP

词的标准化

词的标准化，常用于英文词：

• went，go，going
• fly，flies
• deny，denied，denying
• fast，faster，fastest

意思都类似，如何进行合并？如果处理的是英文词汇,还需要进行stemming或者lemmazation的过程,也就是标准化的过程：

• Stemming，https://tartarus.org/martin/PorterStemmer/

  • went，go，going -> go
  • fly，flies -> fli
  • deny，denied，denying -> deni
  • fast，faster，fastest -> fast
  • 无法保证生成的词在词库里，比如 fli、deni

• Lemmazation

  • 可以确保生成的词在词库里

单词表示

人工智能领域，我们常常需要把文本转换成特征向量、图片转化成向量、语音转化成向量。对于文本来说，如何把一个 word 转化成向量，即 word representation 。

one-hot

常常有如下的方法：词典 [ 我们，去，爬山，今天，你们，昨天，跑步 ]

每个单词的 独热（one-hot）编码 表示：

• 我们：( 1, 0, 0, 0, 0, 0, 0 )
• 爬山：( 0, 0, 1, 0, 0, 0, 0 )
• 跑步：( 0, 0, 0, 0, 0, 0, 1 )
• …

每个句子的 独热（one-hot）编码 表示 ( boolean vector )：

• 我们 今天 去 爬山：( 1, 0, 1, 1, 1, 0, 0, 0 )
• 你们 昨天 跑步：( 0, 0, 0, 0, 0, 1, 1, 1 )
• 你们 又 去 爬山 又 去 跑步 ：( 0, 1, 1, 0, 0, 1, 0, 1 )
• …

每个句子的 独热（one-hot）编码 表示 （ count vector） 可以考虑次数：

• 我们 今天 去 爬山：( 1, 0, 1, 1, 1, 0, 0, 0 )
• 你们 昨天 跑步：( 0, 0, 0, 0, 0, 1, 1, 1 )
• 你们 又 去 爬山 又 去 跑步 ：( 0, 2, 2, 0, 0, 1, 0, 1 )
• …

虽然 count vector 可以考虑词的次数，并不是词出现的次数越多就越重要，并不是出现的次数越少就越不重要。

Tf-idf Representation

$tfidf(w)=tf(d,w)\ast idf(w)$

• $tf(d,w)$：term frequency，文档 d 中 w 的词频

• $idf(w)=log\frac{N}{N(w)}$：inverse document frequency，单词的重要性

  • N：语料库中的文档总数
  • N(w)：词语 w 出现在多少个文档？

例子：

词库 v = [ 今天，上，NLP，课程，的，有，意思，数据，也]

此时有三个文档：

• 今天 上 NLP 课程
• 今天 的 课程 有 意思
• 数据 课程 也 有 意思

进行 tf-idf 编码后：

• 今天 上 NLP 课程 -> $v_1=（1\cdot log\frac{3}{2},1\cdot log\frac{3}{1},1\cdot log\frac{3}{1},1\cdot log\frac{3}{3},0,0,...）$
• 今天 的 课程 有 意思 -> …
• 数据 课程 也 有 意思 -> …

词向量

one-hot 方法有几个缺点：

• 独热便秘是无法表示一个单词具体的含义的
• Sparsity稀疏性，0太多

维度是词库词的个数，并且两个向量的相似度与另外两个向量的相似度是相同的（如果发生正交）。

Distributed Representation

我们：[ 0.1, 0.2, 0.4, 0.2 ]

爬山：[ 0.2, 0.3, 0.7, 0.1 ]

运动：[ 0.2, 0.3, 0.6, 0.2 ]

昨天：[ 0.5, 0.9, 0.1, 0.3 ]

维度是可以自定义的，并且两个向量的相似度与另外两个向量的相似度是不同的，这个独热编码不一样。如何训练出来一个非常好的词向量，是我们的目标。

• 100维的 one-hot 表示法最多可以表达 100 个不同的单词
• 100维的分布式表示法最多可以表达无数个单词

Learn Word Embeddings

将语料库放入 词向量模型 中进行训练，就可以得到 Distributed Representation。这里的词向量模型可以是：

• 传统方式：
  • Skip-Gram
  • Glove
  • CBow
• 考虑上下文：
  • ELMO
  • Bert
  • XLNet

Learn Representation of Words

目标：learn a vector representation for each word w

Distributional hypothesis：you shall know a word by the company it keep

挨在一起的单词相似度更高。

Word Embedding -> Sentence Embedding

我：$[0.2,0.3,0.7,0.1]$

去：$[0.3,0.2,0.1,0.1]$

吃饭：$[0.1,0.2,0.5,0.1]$

我去吃饭：$[\frac{(0.2+0.3+0.1)}{3},\frac{(0.3+0.2+0.2)}{3},\frac{(0.7+0.1+0.5)}{3},\frac{(0.1+0.1+0.1)}{3}]$

Skip-Gram

根据中间的单词预测周围的单词

例子

• 语料库：我 喜欢 nlp

• window size = 1

• maximize：

$$\begin{gathered} maximize:P(喜欢｜我)P(我｜喜欢)P(nlp｜喜欢)P(喜欢｜nlp) \\ =\prod _{w\in text}\prod _{c\in content(w))}P(c|w;\Theta ) \\ w为中心词，c为上下文词 \end{gathered}$$

即：
$$\begin{gathered} optimal\Theta =argmax\prod _{w\in text}\prod _{c\in content(w))}P(c|w;\Theta ) \\ =argmax\sum _{w\in text}\sum _{c\in content(w))}logP(c|w;\Theta ) \end{gathered}$$
其中：
$$\begin{gathered} P(c|w;\theta )=\frac{e^{u_c{v}_w}}{{\sum }_{c^{\prime }}^{}{e}^{u_{c^{\prime }}{v}_w}}\Theta =[u,v] \\ u,v分别代表上下文词和中心词的词向量。 \end{gathered}$$

CBow

根据周围的单词预测中间的单词

Sentence similarity

欧式距离 (不考虑向量的方向)：$d=|s_1-s_2|$
$$\begin{gathered} x=(x_1,x_2,x_3) \\ y=(y_1,y_2,y_3) \\ {d}_E(x,y)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+(x_3-y_3{)}^2} \end{gathered}$$
S1: " 我们 今天 去 爬山 "：( 1, 0, 1, 1, 1, 0, 0, 0 )

S2: " 你们 昨天 跑步 "：( 0, 0, 0, 0, 0, 1, 1, 1 )

S3: " 你们 又 去 爬山 又 去 跑步 " ：( 0, 2, 2, 0, 0, 1, 0, 1 )

$d_E(S_1,S_2)$：句子 $S_1$ 和句子 $S_2$ 的距离。

余弦相似度(最常用)：$Sim=\frac{s_1\cdot s_2}{|s_1|\ast |s_2|}$ 其中 $s_1\cdot s_2$ 是内积，代表两个向量的相似度，分母是归一化的操作。
$$\begin{gathered} x=(x_1,x_2,x_3) \\ y=(y_1,y_2,y_3) \\ {d}_E(x,y)=\frac{x_1\cdot y_1+x_2\cdot y_2+x_3\cdot y_3}{\sqrt{x_1^2+x_2^2+x_3^2}\cdot \sqrt{y_1^2+y_2^2+y_3^2}} \end{gathered}$$

除了这些计算相似度的公式，还有其它的距离公式：

• Mahalanobis Distance
• Chebyshev Distance
• . . .

参考

[1] https://zhuanlan.zhihu.com/p/44107044

[2] https://zhuanlan.zhihu.com/p/114432097

[3] https://www.cnblogs.com/bqtang/p/3693827.html