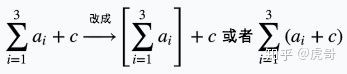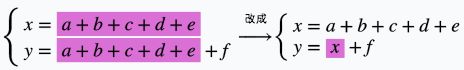手撕 BiLSTM-CRF
文章转载自:
虎哥:https://zhuanlan.zhihu.com/p/97676647
如有侵权,联系删除
目录
网上关于BiLSTM-CRF的资料可谓汗牛充栋;但是扎扎实实给出每一步推导(不跳跃),并结合每一行代码(包括每处张量运算的注释)的文章,至今未见
所以,关于【BiLSTM-CRF的推导和代码部分】你看到的可能是迄今为止最扎实的一个版本
注:我假设你已经熟悉了BiLSTM和CRF的基本原理; 否则,请先【大致浏览】以下材料
CRF: http://homepages.inf.ed.ac.uk/csutton/publications/crftut-fnt.pdf
LSTM: https://colah.github.io/posts/2015-08-Understanding-LSTMs/
BiLSTM-CRF原文: https://arxiv.org/pdf/1508.01991v1.pdf
零、Introduction
本文要介绍的是NLP序列标注领域近年来最经典的文章,百度研究院出品的《Bidirectional LSTM-CRF Models for Sequence Tagging》
本文专注于"手撕"这个模型的【代码和推导细节】,所有背景知识一概省略
一、路线图
Talk is cheap, 直接看代码
链接: https://gist.github.com/koyo922/9300e5afbec83cbb63ad104d6a224cf4
简化解构如下, 我会大致按照执行顺序来讲解:
-
1 从
__main__入手;了解主流程,即构造训练数据集和模型对象 -
2 模型训练
其中涉及求lossneg_log_likelihood()
CRF的分子_score_sentence();
CRF的分母_forward_alg(); 顺便介绍用到的log_sum_exp() -
3 模型推断, 就是前向运算
forward()
其中涉及维特比解码_viterbi_decode()
def log_sum_exp(smat): # 模型中经常用到的一种路径运算的实现
...
class BiLSTM_CRF(nn.Module):
def neg_log_likelihood(self, words, tags): # 求负对数似然,作为loss
...
def _score_sentence(self, frames, tags): # 求路径pair: frames->tags 的分值
...
def _forward_alg(self, frames): # 求CRF中的分母"Z", 用于loss
...
def _viterbi_decode(self, frames): # 求最优路径分值 和 最优路径
...
def forward(self, words): # 模型inference逻辑
...
if __name__ == "__main__":
training_data = [...] # 准备好训练数据和模型
model = BiLSTM_CRF(...)
...
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=1e-4)
for epoch in range(300): # 训练300个epoch
for words, tags in training_data:
model.zero_grad()
model.neg_log_likelihood(words, tags).backward()
optimizer.step()
# 观察训练后的inference结果
with torch.no_grad(): print(model(training_data[0][0]))
二、参数估计(Parameter Estimation)
沿着执行顺序看,__main__下面的主流程就是构造训练数据集和模型对象,然后训练,然后推断;不多说。
看训练逻辑
https://gist.github.com/koyo922/9300e5afbec83cbb63ad104d6a224cf4#file-bilstm_crf-py-L78-L83
def neg_log_likelihood(self, words, tags): # 求一对 在当前参数下的负对数似然,作为loss
frames = self._get_lstm_features(words) # emission score at each frame
gold_score = self._score_sentence(frames, tags) # 正确路径的分数
forward_score = self._forward_alg(frames) # 所有路径的分数和
# -(正确路径的分数 - 所有路径的分数和);注意取负号 -log(a/b) = -[log(a) - log(b)] = log(b) - log(a)
return forward_score - gold_score
-
首先使用LSTM求出了每一帧对应到每种tag的"发射【分值】矩阵"
frames(注意不是【概率】!!! ,这里加起来和不为1;注意CRF跟HMM/MEMM的区别) -
然后,基于
frames和当前的CRF层参数,可以求出指定隐状态路径tags对应的分值gold_score
然后,不限定隐状态路径,求出所有路径对应分值之和forward_score -
最后,根据CRF模型定义,两者相减即可
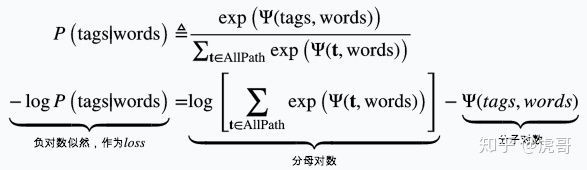
2.1 CRF的分子对数 _score_sentence()
上述 l o g ( Ψ ( t a g s , w o r d s ) ) log(\Psi(tags, words)) log(Ψ(tags,words))可通过函数 _score_sentence()求解
根据CRF模型定义,推导如下:
对应代码
def _score_sentence(self, frames, tags):
tags_tensor = self._to_tensor([START_TAG] + tags, self.tag2ix)
score = torch.zeros(1)
for i, frame in enumerate(frames): # 沿途累加每一帧的转移和发射
score += self.transitions[tags_tensor[i], tags_tensor[i + 1]] + frame[tags_tensor[i + 1]]
return score + self.transitions[tags_tensor[-1], self.tag2ix[END_TAG]] # 加上到END_TAG的转移
※ 注意到上述推导过程中,我在 Σ \Sigma Σ 外面套了一层中括号。
这是为了避免歧义. 例如: ∑ i = 1 3 a i + c \sum_{i=1}^3 ai+c i=1∑3ai+c到底是指 a 1 + a 2 + a 3 + c a1+a2+a3+c a1+a2+a3+c 还是 ( a 1 + c ) + ( a 2 + c ) + ( a 3 + c ) (a1+c)+(a2+c)+(a3+c) (a1+c)+(a2+c)+(a3+c)呢?
这里字母 c c c 不含下标,通常按照前一种方式理解即可。
符号简单的时候,还勉强能看出来;如果复杂一点呢?
相信很多同学都有 类似的被晦涩而充满歧义的数学表达坑过的惨痛经历。
古文是没有断句的,要靠读者的经验来消歧;古人不以糊涂草率为耻,反而将这种所谓“技能”美其名曰“句读”。 e.g. 子曰“民可使由之不可使知之”。断成“民可使由之,不可使知之” v.s. “民可使,由之;不可使,知之”;截然相反的歧义。
如果把代码比作“白话文”,则数学公式表达类似于“文言文”,而且是还没断句的那种。
呼吁大家:从我做起,尽力改善数学表达的可读性
期望能早日看到这个领域的 “胡适、鲁迅、陈独秀、蔡元培”们站出来改善这一局面; 目前我能想到的有以下几个方向,抛砖引玉,欢迎讨论补充:
-
合理命名:
-
尽量使用大家习惯的符号,避免滥用 n , a , b , i , j , . . . n,a,b,i,j,... n,a,b,i,j,... 之类的无意义变量
-
尽量使用容易猜到含义的首字母或者希腊字母作为变量名 e.g. I − > I n i t i a l , T − > T r a n s i t i o n , E − > E m i s s i o n , L − > L e n g t h , △ − > D i f f e n r e n c e I-> Initial, T->Transition, E->Emission, L->Length, △->Diffenrence I−>Initial,T−>Transition,E−>Emission,L−>Length,△−>Diffenrence
-
必要时,使用 多字母的变量名(e.g. “head/tail”), 甚至导入辅助概念(第一枚硬币的颜色 “red/black”) 也是可以的

-
充分注解:
2.2 CRF的分母 _forward_alg()
分母对数 = l o g [ ∑ t ∈ A l l P a t h e x p ( Ψ ( t , w o r d s ) ) ] log[\sum_{t\in AllPath} exp(\Psi(t, words))] log[∑t∈AllPathexp(Ψ(t,words))]
这里有个困难 t ∈ A l l P a t h t\in AllPath t∈AllPath 难以穷举。e.g. 设 len(tags)=5且len(words)=10,则 t 的取值空间是 5 10 5^{10} 510 。
换个思路,不再按照 t t t 求和,而是改为 沿着时间轴做DP
思考一下递推关系:
-
穷举所有长度为L-1的path, 其集合记作 P L − 1 P^{L-1} PL−1
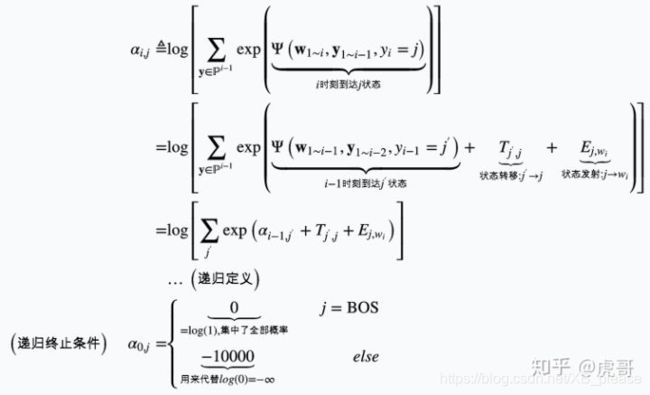
定义 α i , j = l o g [ ∑ y ∈ P i − 1 e x p ( Ψ ( w 1 − i , y 1 − i − 1 , y i = j ) ) ] α_{i,j} = log[\sum_{y\in P^{i-1}} exp(\Psi(w_{1-i}, y_{1-{i-1}}, y_i = j))] αi,j=log[∑y∈Pi−1exp(Ψ(w1−i,y1−i−1,yi=j))] ,即"i时刻到状态j"的所有路径分数的log_sum_exp
至此,我们将待求的"分母对数"化成了 关于 α α α 向量的log_sum_exp形式;只要能DP求出 α α α向量,问题就得到了解决。 α α α的递推关系如下
根据上述推导,观察【单个状态】 α i − 1 , j ′ − > α i , j α_{i-1,j'}->α_{i,j} αi−1,j′−>αi,j 的递推过程:
已知: α i − 1 , j ′ α_{i-1,j'} αi−1,j′ ∀ j ′ − > A l l T a g s \forall j'->AllTags ∀j′−>AllTags
要求: α i , j α_{i,j} αi,j
做法: 加上 j ′ − > j j'->j j′−>j 的状态转移分 和 j ′ − > w i j'->w_i j′−>wi 的发射分;
即 α i , j = l o g [ ∑ j ′ e x p ( α i − 1 , j ′ + j j ′ , j + E j , w i ) ] α_{i,j} = log[\sum_{j'} exp(α_{i-1,j'}+j_{j',j}+E_{j,w_i})] αi,j=log[∑j′exp(αi−1,j′+jj′,j+Ej,wi)]
将上述【单个状态】的推导加以概括,得到【矩阵化】写法; 以1 -> 2时刻为例
对应代码
def _forward_alg(self, frames):
""" 给定每一帧的发射分值; 按照当前的CRF层参数算出所有可能序列的分值和,用作概率归一化分母 """
alpha = torch.full((1, self.n_tags), -10000.0)
alpha[0][self.tag2ix[START_TAG]] = 0 # 初始化分值分布. START_TAG是log(1)=0, 其他都是很小的值 "-10000"
for frame in frames:
# log_sum_exp()内三者相加会广播: 当前各状态的分值分布(列向量) + 发射分值(行向量) + 转移矩阵(方形矩阵)
# 相加所得矩阵的物理意义见log_sum_exp()函数的注释; 然后按列求log_sum_exp得到行向量
alpha = log_sum_exp(alpha.T + frame.unsqueeze(0) + self.transitions)
# 最后转到EOS,发射分值为0,转移分值为列向量 self.transitions[:, [self.tag2ix[END_TAG]]]
return log_sum_exp(alpha.T + 0 + self.transitions[:, [self.tag2ix[END_TAG]]]).flatten()
def log_sum_exp(smat):
"""
参数: smat 是 "status matrix", DP状态矩阵; 其中 smat[i][j] 表示 上一帧为i状态且当前帧为j状态的分值
作用: 针对输入的【二维数组的每一列】, 各元素分别取exp之后求和再取log; 物理意义: 当前帧到达每个状态的分值(综合所有来源)
例如: smat = [[ 1 3 9]
[ 2 9 1]
[ 3 4 7]]
其中 smat[:, 2]= [9,1,7] 表示当前帧到达状态"2"有三种可能的来源, 分别来自上一帧的状态0,1,2
这三条路径的分值求和按照log_sum_exp法则,展开 log_sum_exp(9,1,7) = log(exp(9) + exp(1) + exp(7)) = 3.964
所以,综合考虑所有可能的来源路径,【当前帧到达状态"2"的总分值】为 3.964
前两列类似处理,得到一个行向量作为结果返回 [ [?, ?, 3.964] ]
注意数值稳定性技巧 e.g. 假设某一列中有个很大的数
输入的一列 = [1, 999, 4]
输出 = log(exp(1) + exp(999) + exp(4)) # 【直接计算会遭遇 exp(999) = INF 上溢问题】
= log(exp(1-999)*exp(999) + exp(999-999)*exp(999) + exp(4-999)*exp(999)) # 每个元素先乘后除 exp(999)
= log([exp(1-999) + exp(999-999) + exp(4-999)] * exp(999)) # 提取公因式 exp(999)
= log([exp(1-999) + exp(999-999) + exp(4-999)]) + log(exp(999)) # log乘法拆解成加法
= log([exp(1-999) + exp(999-999) + exp(4-999)]) + 999 # 此处exp(?)内部都是非正数,不会发生上溢
= log([exp(smat[0]-vmax) + exp(smat[1]-vmax) + exp(smat[2]-vmax)]) + vmax # 符号化表达
代码只有两行,但是涉及二维张量的变形有点晦涩,逐步分析如下, 例如:
smat = [[ 1 3 9]
[ 2 9 1]
[ 3 4 7]]
smat.max(dim=0, keepdim=True) 是指【找到各列的max】,即: vmax = [[ 3 9 9]] 是个行向量
然后 smat-vmax, 两者形状分别是 (3,3) 和 (1,3), 相减会广播(vmax广播复制为3*3矩阵),得到:
smat - vmax = [[ -2 -6 0 ]
[ -1 0 -8]
[ 0 -5 -2]]
然后.exp()是逐元素求指数
然后.sum(axis=0, keepdim=True) 是"sum over axis 0",即【逐列求和】, 得到的是行向量,shape=(1,3)
然后.log()是逐元素求对数
最后再加上 vmax; 两个行向量相加, 结果还是个行向量
"""
vmax = smat.max(dim=0, keepdim=True).values # 每一列的最大数
return (smat - vmax).exp().sum(axis=0, keepdim=True).log() + vmax
三、推断(Inference)
推断逻辑很直观,就是过一遍LSTM拿到每一帧的发射状态分布;然后跑viterbi解码得出最优路径和分值。
def forward(self, words): # 模型inference逻辑
lstm_feats = self._get_lstm_features(words) # 求出每一帧的发射矩阵
return self._viterbi_decode(lstm_feats) # 采用已经训好的CRF层, 做维特比解码, 得到最优路径及其分数
3.1 维特比解码 _viterbi_decode()
我假设你熟悉CRF算法;所以viterbi本身不用介绍了。 说一下跟前向求CRF分母对数时的小小区别:这里除了要迭代更新 α α α 以外,还要追踪每一帧的每个状态的最优“上一步”来自于哪里。因此,可以看到第9行的log_sum_exp()上方的第8行还记下了argmax
def _viterbi_decode(self, frames):
backtrace = [] # 回溯路径; backtrace[i][j] := 第i帧到达j状态的所有路径中, 得分最高的那条在i-1帧是神马状态
alpha = torch.full((1, self.n_tags), -10000.)
alpha[0][self.tag2ix[START_TAG]] = 0
for frame in frames:
# 这里跟 _forward_alg()稍有不同: 需要求最优路径(而非一个总体分值), 所以还要对smat求column_max
smat = alpha.T + frame.unsqueeze(0) + self.transitions
backtrace.append(smat.argmax(0)) # 当前帧每个状态的最优"来源"
alpha = log_sum_exp(smat) # 转移规律跟 _forward_alg()一样; 只不过转移之前拿smat求了一下回溯路径
# 回溯路径
smat = alpha.T + 0 + self.transitions[:, [self.tag2ix[END_TAG]]]
best_tag_id = smat.flatten().argmax().item()
best_path = [best_tag_id]
for bptrs_t in reversed(backtrace[1:]): # 从[1:]开始,去掉开头的 START_TAG
best_tag_id = bptrs_t[best_tag_id].item()
best_path.append(best_tag_id)
return log_sum_exp(smat).item(), best_path[::-1] # 返回最优路径分值 和 最优路径
四、总结
本文给出了 BiLSTM-CRF用作序列标注算法的 详细推导步骤,并在PyTorch官方教程的基础上 修改成了矩阵化写法;同时,给出了一份注释详尽的教学代码。
单步调试跟一遍,相信你会有不小收获。
happy coding, 祝好运!
参考文献
BiLSTM-CRF原文: https://arxiv.org/pdf/1508.01991v1.pdf
PyTorch官方教学代码: https://pytorch.org/tutorials/beginner/nlp/advanced_tutorial.html
矩阵化推导: https://zhuanlan.zhihu.com/p/44042528