10_分类算法-朴素贝叶斯算法应用场景、联合概率和条件概率、朴素贝叶斯介绍、朴素贝叶斯公式、朴素贝叶斯模型流程、半朴素贝叶斯分类器、sklearn朴素贝叶斯实现API、拉普拉斯平滑、优缺点、面试题
1、应用场景
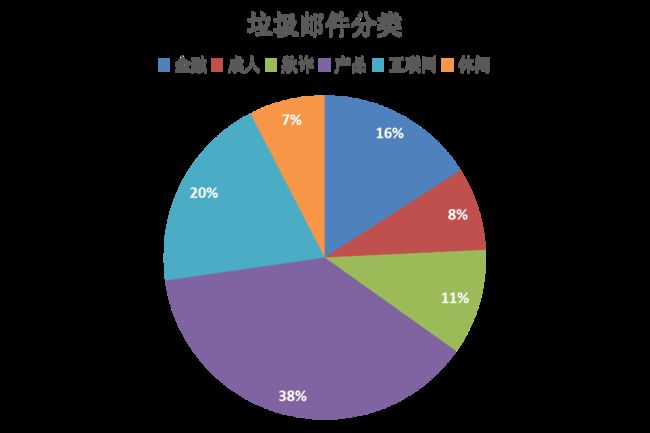
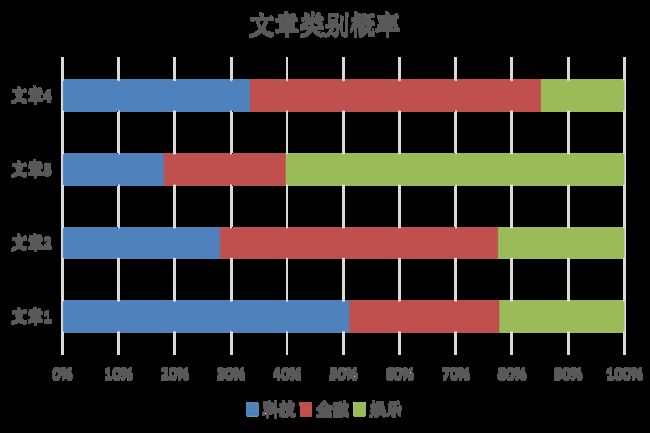
1.1 垃圾邮件分类
2、概率基础
1、女神喜欢的概率?
2、职业是程序员并且体型匀称的概率?
3、在女神喜欢的条件下,职业是程序员的概率?
4、在女神喜欢的条件下,职业是产品,体重是超重的概率?
2.1 联合概率和条件概率
以下主要来自:https://blog.csdn.net/sinat_30353259/article/details/80932111
联合概率:包含多个条件,且所有条件同时成立的概率。记作:P(A,B)
条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率。记作:P(A | B),读做"在B条件下A的概率"
若只有两个事件A,B,那么:

特性:P(A1,A2|B) = P(A1|B)P(A2|B)
注意:此条件概率的成立,是由于A1,A2相互独立的结果。
全概率公式:表示若事件A1,A2,…,An构成一个完备事件组且都有正概率,则对任何一个事件B都有公式成立。
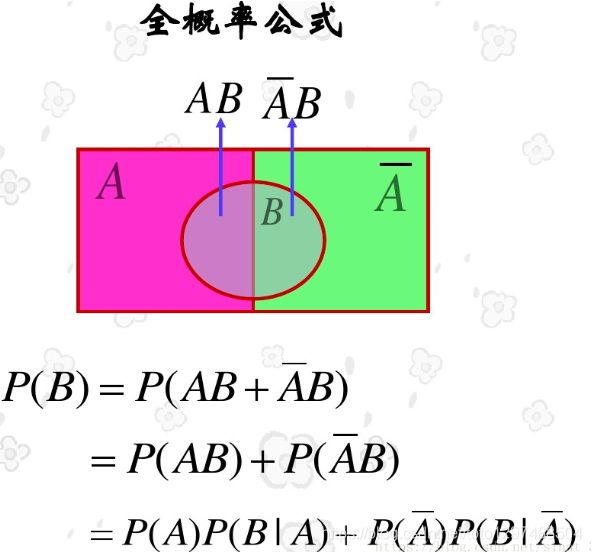
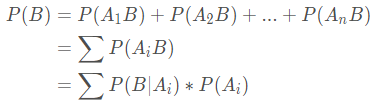
3、朴素贝叶斯介绍
贝叶斯公式是将全概率公式带入到条件概率公式当中, 对于事件Ak和事件B有:
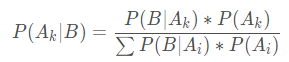

朴素贝叶斯公式:
![]()
【例2】一起汽车撞人逃跑事件,已知只有两种颜色的车,比例为蓝色15% 绿色85%,目击者指证是蓝车,但根据现场分析,当时那种条件目击者看正确车的颜色的可能性是80%,那么,肇事的车是蓝车的概率到底是多少。
答案:
设A={目击者看到车是蓝色的}, B={车的实际颜色是蓝色}
P(A)=80%×15%+20%×85%=29%
即: 车是蓝色(15%)×目击者看正确(80%)+车是绿色(85%)×目击
者看错了(20%)
P(AB)=80%×15%=12%
即: 车是蓝色(15%)×目击者看正确(80%)
P(B|A)=P(AB)/P(A)=12%/29%≈41%
3.2 朴素贝叶斯模型流程
朴素贝叶斯的基本方法: 在统计数据的基础上,依据条件概率公式,计算当前特征的样本属于某个分类的概率,选最大的概率分类。
对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别:
①计算流程:

例题:


②三个阶段:
第一阶段——准备阶段, 根据具体情况确定特征属性, 对每个特征属性进行适当划分, 然后由人工对一部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段, 其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段——分类器训练阶段, 这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计, 并将结果记录。 其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段, 根据前面讨论的公式可以由程序自动计算完成。
第三阶段——应用阶段。 这个阶段的任务是使用分类器对待分类项进行分类, 其输入是分类器
和待分类项, 输出是待分类项与类别的映射关系。这一阶段也是机械性阶段, 由程序完成。
3.3 拉普拉斯平滑
4 半朴素贝叶斯分类器
概念
在朴素的分类中, 我们假定了各个属性之间的独立,这是为了计算方便,防止过多的属性之间的依赖导致的大量计算。这正是朴素的含义,虽然朴素贝叶斯的分类效果不错,但是属性之间毕竟是有关联的, 某个属性依赖于另外的属性, 于是就有了半朴素贝叶斯分类器:
5、朴素贝叶斯介绍(补)
5.1 贝叶斯公式
- P©:每个文档类别的概率(某文档类别词数/总文档词数)
- P(W|C):给定类别下特征(被预测文档中出现的词)的概率。
计算方式:P(F1|C) = Ni / N
Ni为该F1词在C类别所有文档中出现的次数
N为所属类别C下的文档所有词出现的次数和
- P(F1,F2,…)预测文档中每个词的概率。
训练集统计结果(指定统计词频):
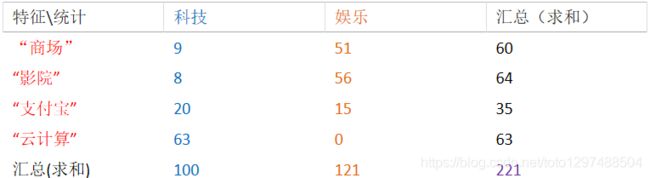
现有一篇被预测文档:出现了影院,支付宝,云计算,计算属于科技、娱乐的类别概率?

思考:属于某个类别为0,合适吗?
5.2 拉普拉斯平滑
问题:从上面的例子我们得到娱乐概率为0,这是不合理的,如果词频列表里面有很多出现次数都为0,很可能计算结果都为零

5.3 sklearn朴素贝叶斯实现API
sklearn.naive_bayes.MultinomialNB(alpha = 1.0, fit_prior= True, class_prior= None)
概念解释:
针对多项式模型的朴素贝叶斯(Naive Bayes)分类器。
多项式朴素贝叶斯分类器适合离散特征的分类问题。(例如:文本分类中的单词计数)。
多项式分布一般要求特征计数是整数。然而,实际应用中,如tf-idf这种分类计数也可能有效。
参数
| Parameters | 数据类型 | 意义 |
|---|---|---|
| alpha | float,optional (default=1.0) | 附加的平滑参数(Laplace/Lidstone) ,0是不平滑(这个就是拉普拉斯平滑系数) |
| fit_prior | boolean,optional (default=True) | 不管是否学习经典先验概率,如果False则采用uniform先验 |
| class_prior | array-like, size (n_classes,), optional (default=None) | 类别的先验概率,一经指定先验概率不能随着数据而调整 |
属性Attributes
| Attributes | 数据类型 | 意义 |
|---|---|---|
| class_log_prior_ | array,shape(n_classes,) | 平滑的经验对数概率 |
| intercept_ | array,shape(n_classes,n_features) | class_log_prior_的镜像将MultinomialNB解释为线性模型 |
| featur_log_prob_ | array, shape (n_classes, n_features) | 特征的经验对数概率P(X_i |
| coef_ | array, shape (n_classes, n_features) | feature_log_prob_镜像用于将MultinomialNB解释为线性模型 |
| class_count_ | array,shape(n_classes,) | 拟合过程中每个类遇到的样本数,这个值用给定的权重值作为权重 |
| feature_count_ | array, shape (n_classes, n_features) | 拟合过程中每个(类、特征)遇到的样本数,这个值用给定的权重值作为权重 |
方法Methods
1、fit(self, X, y[, sample_weight])
根据X,y拟合NB分类器
2、get_params(self[, deep])
获取这个评估器的参数
3、partial_fit(self, X, y[, classes, sample_weight])
对一批样本进行增量拟合
4、predict(self, X)
在测试向量X构成的数组上演示分类性能
5、predict_log_proba(self, X)
返回针对测试向量X的对数概率估算
6、predict_proba(self, X)
返回针对测试向量X的概率估算
7、score(self, X, y[, sample_weight])
返回针对特殊样本的准确性
9、set_params(self, **params)
为此评估器设置参数
案例一:
1、Out-of-core classification of text documents
2、Classification of text documents using sparse features
案例二
A:朴素贝叶斯算法案例
1、sklearn20新闻分类
2、20个新闻组数据集包含20个主题的18000个新闻组帖子
B:朴素贝叶斯案例流程
1、加载20类新闻数据,并进行分割
2、生成文章特征词
3、朴素贝叶斯estimator流程进行预估
C:代码
from sklearn.datasets import fetch_20newsgroups
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics import classification_report
def naviebayes():
"""
朴素贝叶斯进行文本分类
:return: None
"""
news = fetch_20newsgroups(subset='all')
# 进行数据分割
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
# 对数据集进行特征抽取
tf = TfidfVectorizer()
# 以训练集当中的词的列表进行每篇文章重要性统计['a','b','c','d']
x_train = tf.fit_transform(x_train)
print(tf.get_feature_names())
x_test = tf.transform(x_test)
# 进行朴素贝叶斯算法的预测
mlt = MultinomialNB(alpha=1.0)
print(x_train.toarray())
mlt.fit(x_train, y_train)
y_predict = mlt.predict(x_test)
print("预测的文章类别为:", y_predict)
# 得出准确率
print("准确率为:", mlt.score(x_test, y_test))
print("每个类别的精确率和召回率:", classification_report(y_test, y_predict, target_names=news.target_names))
return None
if __name__ == "__main__":
naviebayes()
输出结果:
在这里插入代码片
5.4 朴素贝叶斯分类优缺点
优点:
1、朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
2、对缺失数据不太敏感,算法也比较简单,常用于文本分类。
3、分类准确度高,速度快
缺点:
1、需要知道先验概率P(F1,F2,…|C),因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
6、朴素贝叶斯的面试题
1、朴素贝叶斯与LR的区别
简单来说:朴素贝叶斯是生成模型,根据已有样本进行贝叶斯估计学习出先验概率P(Y)和条件概率P(X|Y),进而求出联合分布概率P(XY),最后利用贝叶斯定理求解P(Y|X), 而LR(逻辑回归)是判别模型,根据极大化对数似然函数直接求出条件概率P(Y|X);朴素贝叶斯是基于很强的条件独立假设(在已知分类Y的条件下,各个特征变量取值是相互独立的),而LR则对此没有要求;朴素贝叶斯适用于数据集少的情景,而LR适用于大规模数据集。
2、朴素贝叶斯“朴素”在哪里?
简单来说:利用贝叶斯定理求解联合概率P(XY)时,需要计算条件概率P(X|Y)。在计算P(X|Y)时,朴素贝叶斯做了一个很强的条件独立假设(当Y确定时,X的各个分量取值之间相互独立),即P(X1=x1,X2=x2,…Xj=xj|Y=yk) = P(X1=x1|Y=yk)P(X2=x2|Y=yk)…*P(Xj=xj|Y=yk)。
3、 在估计条件概率P(X|Y)时出现概率为0的情况怎么办?
简单来说:引入λ,当λ=1时称为拉普拉斯平滑。
4、朴素贝叶斯的优缺点
优点:对小规模的数据表现很好,适合多分类任务,适合增量式训练。
缺点:对输入数据的表达形式很敏感(离散、连续,值极大极小之类的)。
重点:
面试的时候怎么回答朴素贝叶斯呢?
首先朴素贝斯是一个生成模型(很重要),其次它通过学习已知样本,计算出联合概率,再求条件概率。
生成模式和判别模式的区别:
生成模式: 由数据学得联合概率分布,求出条件概率分布P(Y|X)的预测模型;
常见的生成模型有:朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型(LDA)、限制玻尔兹曼机
**判别模式:**由数学得决策函数或条件概率分布作为预测模型。
常见的判别模型有:K近邻、SVM、决策树、感知机、线性判别分析(LDA)、线性回归、传统的神经网络、逻辑斯蒂回归、boosting、条件随机场。
其它(非常好的一篇文章):
《机器学习实现》
https://blog.csdn.net/TeFuirnever/article/details/100108341
打个赏呗,您的支持是我坚持写好博文的动力。
![]()