详解 Hough 变换(上)基本原理与直线检测
Hough 变换原理与应用
前言: 详细介绍了 Hough 变换的基本思想、基本原理和应用等。其中大多都是自己的理解,难免有偏差,仅供参考。
文章目录
- Hough 变换原理与应用
-
- 1. 基本概述
-
- 1.1 一些基本问题
- 1.2 以例子说明
-
- 1.2.1 例子1:直线 y = k x + b y = kx + b y=kx+b 到参数空间的变换(k,b为定值,如k=2,b=4)
- 1.2.2 例子2:极坐标下的直线到参数空间的变换
- 1.2.3 例子3:圆到参数空间的变换
- 2. Hough 直线检测
-
- 2.1 问题
- 2.2 思路
- 2.3 总结
- 2.4 提升
-
- 2.4.1 实际问题
- 2.4.2 求解思路
- 2.4.3 自编程实现
- 2.5 openCV对应代码解读
1. 基本概述
1.1 一些基本问题
Hough 变换简单概括就是原空间到参数空间的变换。
以一条直线为例,常用直线方程为 y = k x + b y = kx+b y=kx+b ,这个是原空间。在这个直线方程里,x 和 y 是变量,k和b为直线方程参数。注意参数不是固定的,数量也不是固定的,比如这个直线不一定非要用 k,b (斜率和截距)这两个参数,下面会有举例说明。
何为到参数空间的变换呢?
直接了当地说就是,把参数当作变量(即坐标轴)。上面直线例子而言,就是把 k,b 当作横纵坐标构建的空间。注意,这一变换并非坐标系的变换(如:不是笛卡尔坐标向极坐标的变换;两者本质就不一样),Hough变换是始终以笛卡尔坐标系为基础,只是换了坐标轴(新空间中,坐标轴换成了原空间表达式中的参数,也是因此新空间叫参数空间。)
为何要变换到参数空间呢?
原空间中一些事物具有很强的关联性,但在原空间不好观察和把握,因此考虑从别的视角来表述它们关联性。参数空间就是一种,还有类似的傅里叶变换等等。所以,可以说,我们变换此空间,是为了更直观地揪出原坐标系下一系列点间的共同特点(或者说联系)。至于为什么选择参数空间,别问,问就是第一个想出这点的数学家的智慧和创新。并且,”很巧”的是,它在处理一些问题上确实很管用。
既然说参数选择不是固定的,如何选择最佳参数来构成参数空间?
这个不用操心,针对一些特定任务和问题,前人已经给出了答案了。
1.2 以例子说明
下面以三个例子说明上述自己理解得出的重点。
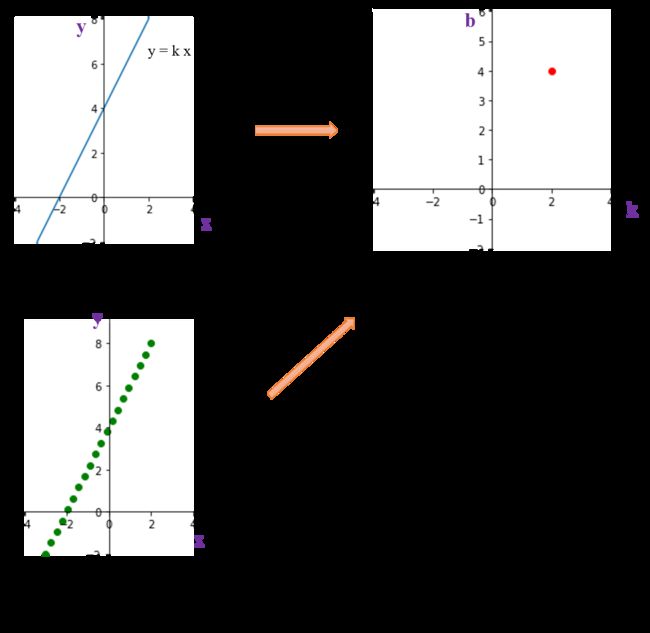
1.2.1 例子1:直线 y = k x + b y = kx + b y=kx+b 到参数空间的变换(k,b为定值,如k=2,b=4)
事实上,使用这样例子并不好,容易给人带来误解,但又不得不从该例子说起。之所以说容易带来误解,原因在于:
我们遇到的问题,往往都是考察原坐标系下所给出的一系列点的关系问题。即基于点,去将这些点变换到参数空间;这个例子的表述,恰恰与此过程相反,该例子表述是已知结果(这些点是在一条直线上),去说明参数变换这回事。
两个是因果倒置的问题。这么说有些难以理解,下面例子会说明上面两句话要表达的含义。
我们考察直线到其参数空间的变换,这里参数就选择 k,b,变换如下图(a)(b)所示。
我们这样表述:左侧原空间下,对于直线 y = k x + b y = kx + b y=kx+b ,将 k , b k,b k,b 当作坐标轴的话,得到右侧参数空间,**该直线就对应于右侧空间一点 ( k , b ) (k,b) (k,b) ** 。这样表述有些别扭,因为常规上,我们都是把问题落脚在点上,毕竟计算机存储和处理的都是离散点数据。
因此修改说: 左侧原空间下,直线 y = k x + b y=kx+b y=kx+b 上的点 对应 右侧参数空间中一点 ( k , b ) (k, b) (k,b),如图©到(b)所示。 但这样说的话,同样别扭,因为这句话是错的。
Hough 变换不是常规的映射,不是点对点的对应关系,不是函数式的 f(x)。这点也可以说明它跟坐标系间变换有本质区别。
左侧原空间上的任意一点如 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),对应到右侧,不会是一个点,事实上是一条线。因为右侧表示的是直线的斜率和截距,而经过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 的直线有无数条,也就对应着无数的 k 和 b。那是否意味着左侧这 ( x 0 , y 0 ) (x_0, y_0) (x0,y0) 点,对应到右侧,就是充满坐标轴的所有点?当然不是,因为 k,b 虽然是随机的,取值可以 [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞],但它俩不是各自随机,两者是有关系的。因为我们前面前提是经过 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 点的直线,即
y = k ( x − x 0 ) + y 0 y = k (x-x_0) + y_0 y=k(x−x0)+y0
说明:用这个 y = kx + b 这个式子不好,因为后面例子都是把 x、y 放到一侧,两者式子下,过点限制条件是由差别的。使用 y − k x = b y-kx = b y−kx=b或 y − k x − b = 0 y-kx-b=0 y−kx−b=0 理解更好,这样的话,限制条件就是
y − k x = y 0 − k x 0 或 y − k x − b = y 0 − k x 0 − b y - k x= y_0-k x_0\ \ \ \ 或 \ \ \ y-kx-b = y_0-kx_0 -b y−kx=y0−kx0 或 y−kx−b=y0−kx0−b
也即
y − k x = ( y 0 − k x ) y - kx = (y_0-kx) y−kx=(y0−kx)
这里会衍生出一个问题,即好像一个参数 k 就可以确定这一直线了。到这节最后会说到这个问题。先忽略之,或自己加以理解。
依据上式,也就是以 k, y 0 − k x 0 y_0-kx_0 y0−kx0 为参数,即 k 当横轴, y 0 − k x 0 y_0-kx_0 y0−kx0 当纵轴,或者写为我们更常见的
b = − k x 0 + y 0 b = -kx_0+y_0 b=−kx0+y0
其中,b为纵轴,k为横轴。整个过程如下图(a)(b)所示
反过来,参数空间一点,就对应于原空间里 斜率为 k,截距为 b 的直线。
总结一下,这两个空间的关系可以这样表述:左侧原空间的直线对应右侧参数空间一点;左侧原空间一点对应右侧空间一条直线。这是比较有意思的相互关系,圆形变换其实也有这个特点。参数即变量,变量即参数 的感觉。
基于此,我们就把刚才别扭的表述,说得准确些:对于左侧直线,我们用斜率 k 和截距 b 就可以描述它,并且唯一确定它,因此若建立一个斜率、截距空间,点(k,b)就可以表征一条原空间下斜率为 k 截距为 b 的直线。
那么是不是参数只能选择 k,b 呢?显然不是,比如你就可以选择 参数空间里横坐标为 k+b, 纵坐标为 b,同等效果。但一般,参数选择要为计算、理解方便服务。
假设,我们发挥了自己的想象,采取了如下两个参数,即圆心到直线的距离 d 和 这个垂线的角度 θ \theta θ,如下图所示。首先,我们明确的是,这两个参数是否可以唯一确定地表示这一直线?答案当时是肯定的,那么这个参数就能用。
那么,问题就来了,如果以 d , θ d, \theta d,θ 为参数空间横纵坐标,那应该是怎样的。我们下面来考察一下:
首先,我们先把这条直线用 d 和 θ \theta θ 表示出来,这个是高中数学题了,就不推导了(求解思路就是用 d 和 θ \theta θ 表征线上任意一点)。直接给出答案,这条线可以这么表示(这里没有常规地把 y 放在左侧,为了美观)
d = x c o s θ + y s i n θ d = xcos\theta + ysin\theta d=xcosθ+ysinθ
同样的方法,对于无数 d d d 和 θ \theta θ ,我们要满足原空间里经过 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),即
x 0 cos θ + y 0 sin θ = x cos θ + y sin θ x_0\cos\theta+y_0\sin\theta=x\cos\theta+y\sin\theta x0cosθ+y0sinθ=xcosθ+ysinθ
也即有
d = x 0 cos θ + y 0 sin θ d = x_0\cos\theta + y_0\sin\theta d=x0cosθ+y0sinθ
这里体现了 d 是有取值范围的。
根据三角函数的和差角公式,可以写成
d = x 0 + y 0 s i n ( θ + ψ ) d = \sqrt {x_0+y_0}sin(\theta+\psi) d=x0+y0sin(θ+ψ)
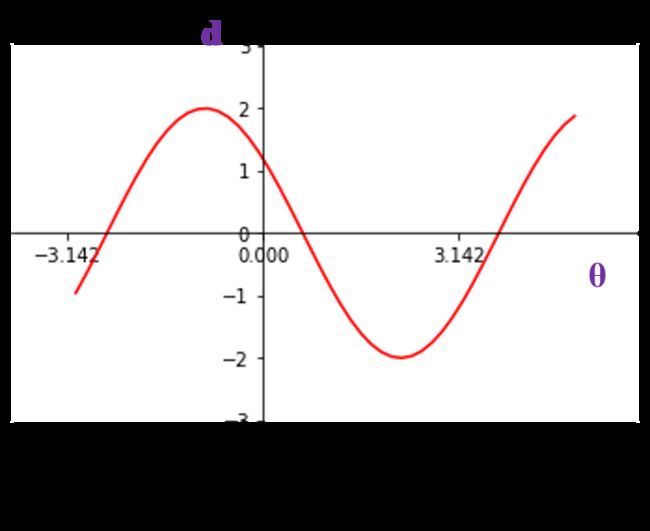
其中, ψ \psi ψ为常数,且 ψ = arctan ( x 0 y 0 ) \psi=\arctan(\frac{x_0}{y_0}) ψ=arctan(y0x0)。最终,我们就可以得到原空间直线上一点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0) ,在上述 d d d 和 θ \theta θ 参数空间下(以d为纵轴, θ \theta θ 为横轴),所表示的东西。是什么呢?是一条正弦曲线。如下图 (b) 所示
也就是说,在原空间里的任意一点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0),如果变换到上述 d , θ d,\theta d,θ 参数空间里,就是一条正弦曲线。同样是点对应线的关系。
上面是直接给出了使用 d d d 和 θ \theta θ 参数,一个是截距一个是角度,显得很突兀。但实际上,使用 d 和 θ \theta θ 参数,应用十分广泛,本质上,它是参考极了坐标的表达,另一方面,其应用广泛的原因在于 d 和 θ \theta θ 都是有范围的,后面图像直线检测实例中会讲到。
上述只是直接给出了结果,是为了避免一些人将它与直角坐标系到极坐标系变换相混淆。下面给出推导:
使用极坐标系表示直角坐标里的点,有个对应关系,即
x = ρ cos θ , y = ρ sin θ x = \rho \cos \theta\ \ \ ,\ y= \rho \sin \theta x=ρcosθ , y=ρsinθ
变换,即
x cos θ = ρ cos 2 θ , y sin θ = ρ sin 2 θ x\cos \theta = \rho \cos^2 \theta\ \ ,\ \ \ y\sin\theta = \rho\sin^2\theta xcosθ=ρcos2θ , ysinθ=ρsin2θ
两等式累加,即
x cos θ + y sin θ = ρ x\cos\theta+y\sin\theta = \rho xcosθ+ysinθ=ρ
也就是上面我们有提到的用 d d d 和 θ \theta θ 表示的直线公式。注意,这里的 ρ \rho ρ 如果要是用于变换到参数空间,表示的不是直角坐标系里的一点到原点距离,而是 过该点且垂线倾角为 θ \theta θ 的直线距原点的距离, θ \theta θ 同理。 ρ , θ \rho,\theta ρ,θ 要是用于点变换到极坐标系下,就是我们常规表示,而且此时是点对点关系。再次强调两者不同点。
总结以上:原空间一点变换到参数空间的结果会随参数选择而变化,参数选择往往是基于计算方便、基于自己目的。
1.2.2 例子2:极坐标下的直线到参数空间的变换
问题来了,极坐标下直线一般方程是什么?同样是高中问题。
直角坐标下
y = k x + b y = kx + b y=kx+b
使用常规推导,即 y = ρ sin θ , x = ρ cos θ y=\rho\sin\theta,x=\rho\cos\theta y=ρsinθ,x=ρcosθ,带入
ρ sin θ = k ρ cos θ + b \rho\sin\theta = k\rho\cos\theta + b ρsinθ=kρcosθ+b
看着别扭,把 k 和 b 换下,即变成形如下式的形式
ρ ( sin θ − m cos θ ) − n = 0 \rho(\sin\theta-m\cos\theta)-n = 0 ρ(sinθ−mcosθ)−n=0
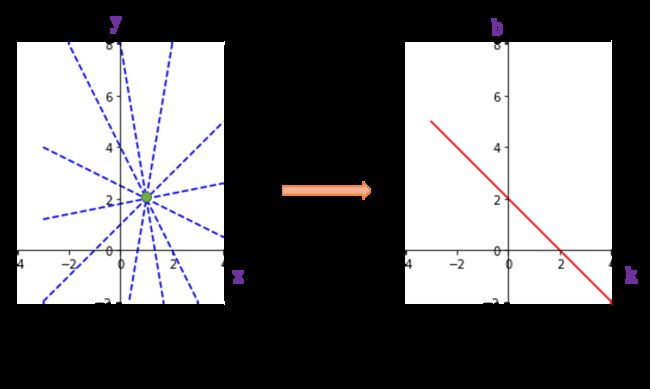
其中,m,n 为定值。也即 m,n 知道后就可以确定极坐标系下唯一直线,因此可以用 m,n 构建该极坐标系下直线的参数空间,即对应于一点(m,n)。只是它的物理意义在坐标系(极坐标系)里不那么看得出来。m,n 的物理意义是,该直线(在极坐标系下)映射到直角坐标系下的斜率和截距。贴个极坐标系下直线图
上式也可以利用三角函数的和差公式变换下,即得
ρ 1 + m 2 s i n ( θ − ψ ) − n = 0 \rho\sqrt{1+m^2} sin(\theta-\psi) -n=0 ρ1+m2sin(θ−ψ)−n=0
也即
ρ sin ( θ − ψ ) = n 1 + m 2 \rho\sin(\theta-\psi)=\frac{n}{\sqrt{1+m^2}} ρsin(θ−ψ)=1+m2n
换下参数,即
ρ sin ( θ + α ) = b \rho\sin(\theta+\alpha) = b ρsin(θ+α)=b
其中, α , b \alpha,b α,b 为常数,同样, α , b \alpha,b α,b 知道后就可以确定极坐标系下唯一直线,同样可以用它构建参数空间。
三个小问题:
-
上面以 α , b \alpha,b α,b 为参数,变换到参数空间后,形状是什么?好奇的自行探究吧。
-
这里的 α , b \alpha,b α,b 可能不能随便取值,换句话说,并不是随意两个 α , b \alpha,b α,b 都可以表示一条直线。因为从公式演化来看,两者都是受 m,n 控制,自由度受控,可能有些 α , b \alpha,b α,b 是无效的,但可以确定的是,极坐标内任意直线都可以找到一组 α , b \alpha,b α,b 与之唯一对应。感觉是如此,不再去印证。
-
是否可以考虑 参数 α , b \alpha,b α,b 用极坐标系表示?即用极坐标系表示参数空间。我想应该是可以的。这是个有意思的问题。但常规上,都是在笛卡尔坐标系下。同样不再去深究。
1.2.3 例子3:圆到参数空间的变换
有了上面的经验,我们考察一下圆。前面已经说过,表达形式不同,可选参数也是多样的。这里只给出常用的参数选择。
圆的一般方程(只考虑笛卡尔坐标系下):
( x − a ) 2 + ( x − b ) 2 = r 2 (x-a)^2+(x-b)^2 = r^2 (x−a)2+(x−b)2=r2
即圆心O坐标为 ( a , b ) (a,b) (a,b),半径为 r r r。
选择 a , b , r a,b,r a,b,r 为参数,注意,这里验证了前面提到的 对于一些问题参数数量也是不一样。
按照前面对直线考察相同的步骤,参数空间里 一点 (a,b,r) 就可以表示原空间里这一圆。不同之处在于,这里上升到了三维坐标。
同样考察对于原空间圆上一点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0) ,与直线相同的思路,经过该点有无数的圆,不同圆心O、半径r就对应着不同的过该点的圆。但同样(a,b,r)不是随意的,而是满足过 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 这一基本条件,即
( x 0 − a ) 2 + ( y 0 − b ) 2 = r 2 (x_0-a)^2+(y_0-b)^2=r^2 (x0−a)2+(y0−b)2=r2
这个也就是选择 a,b,r 作为坐标轴的参数空间下方程。写得顺眼点就是
( a − x 0 ) 2 + ( b − y 0 ) 2 = r 2 (a-x_0)^2 + (b-y_0)^2 = r^2 (a−x0)2+(b−y0)2=r2
更顺眼点,即
( x − x 0 ) 2 + ( y − y 0 ) 2 = z 2 (x-x_0)^2 + (y-y_0)^2 = z^2 (x−x0)2+(y−y0)2=z2
这个方程不就是圆锥方程吗。
参考直线时的表述,我们就可以说:过原空间一点的所有圆 对应于 参数空间里的一个圆锥。
如下图(a)(b)所示
【参考Fig.2自己想象吧,用python画太费劲了,懒。想象:左图(a)是一个点,然后有无数过该点的圆(用虚线表示);右图(b)是一个圆锥。当然也可以有志之士帮忙画一下】
事实上,不如我们把两者综合起来说,即
对于原空间坐标中的一点,如果我们考察对象是 过该点的直线,那么对应于参数空间里,就是一条直线;如果我们考察对象是 过该点的圆,那么对应于参数空间里,就是一个圆锥
两个小问题:
- 维度相较于考察对象为直线时增加了一个,是不是很神奇?自行见解。
- 一个点对应了参数空间的一个圆锥,后面应用时(Hough圆检测),计算量会非常非常大。因此一般不会直接应用,会有改进或别的思路。下面圆形检测部分会详解。
一个有意思的东西:
换个思路表示圆形,即
x = a + r cos θ \cos\theta cosθ
y = b + r sin θ \sin\theta sinθ
上面消去了 θ \theta θ ,会变成了圆一般方程 ( x − a ) 2 + ( x − b ) 2 = r 2 (x-a)^2+(x-b)^2 = r^2 (x−a)2+(x−b)2=r2, 这里我们消去r试试,即变成
y − b = ( x − a ) tan θ y-b = (x-a)\tan\theta y−b=(x−a)tanθ
如果以 a , b , θ a,b,\theta a,b,θ 为参数会怎样呢?一个更有意思的东西:
对于原空间中一点,考察经过该点的所有圆,事实上使用 (a,b) 就可以唯一表示一个圆了,即圆心为(a,b),且经过该点,就已经确定唯一圆了,即只考虑参数 a,b 不就够了吗?
换个更简单的,对于原空间一点,考察经过该点的所有直线,事实上使用斜率 k 就可以唯一表示一条线了,即斜率为k,且经过该点,截距自然而然就确定了。那只考虑参数 k 不就够了吗?为什么参数空间里还要使用两个参数 k,b 来确定经过该点唯一直线。
其实这个问题有些诡辩的意味。稍微思考一下就可以反驳,如果仅用 k 表达,也即参数空间是个一维坐标轴,反推一下,参数空间里一个 k 能表达一条唯一的线吗?显然不能。加入b的原因,就可以简单理解为 是为了把经过该点的信息囊括进去。
更简单直白点就是,参考例子 1 ,实际上 b 并不是单独参数,它只是 k的函数,即f(k),如例子1中的纵轴其实是 y 0 − k x 0 y_0-kx_0 y0−kx0。其目的就是为了表达它有个限制条件,即要经过 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)。
圆形Hough下,同样的原因。
至此,或许对 Hough 变换有了那么一点理解,或者说,有那么点印象了。
下面就直入主题,Hough变换的直线检测和圆检测,以及改进后的其它检测。
2. Hough 直线检测
将前面的结论再说一遍:
对于原空间里的一点,过该点有无数的直线,每条直线唯一对应着参数空间中的一点,而所有直线就对应参数空间里无数的点,这些无数点连起来就是一条直线 o r or or一条正弦线 o r . . . or... or...(取决于你选择的参数)。
先从解决一个简单问题入手。
2.1 问题
如何基于上述 Hough 变换的特点,检测三个点,即 a ( 1 , 2 ) , b ( 3 , 4 ) , c ( − 1 , 0 ) a(1, 2),b(3, 4),c(-1, 0) a(1,2),b(3,4),c(−1,0) 是否在一条直线上?
2.2 思路
根据上面 Hough 直线变换的特点,这里使用 k,b 参数进行分析说明。
先考察 a(-1, 0)点,经过该点有无数的线,映射到 k,b 参数空间是一条直线。而 k,b 空间上该线一点也就对应于原空间这无数线中的其中一条。如下图(b)中红点,就对应于原空间红线。
下面给出参数空间曲线求解过程(可参考 例子1 过程):
经过 a(1,2) 点的所有直线可表示为:
y = k ( x − 1 ) + 2 y = k(x-1)+2 y=k(x−1)+2
即
y = k x − k + 2 y = kx-k+2 y=kx−k+2
则参数空间中,横坐标为 k,表示原空间的直线斜率;纵坐标为 -k+2 ,表示原空间的直线截距,记为b。则参数空间中,线方程就是
y = − x + 2 y = -x + 2 y=−x+2
即 Fig.4 中图(b)所示。该线上每一点,对应左侧过点 a(1,2) 一条线。如红色所示。
同理方法,对于 b,c 点做一样的参数空间变换,最后结果如 Fig.5 所示
右侧参数空间里,有个特殊点 (1,1),参数空间里三个线都经过这点。也即有
- 对于 a ,该特殊点含义是,原空间中,有个 斜率为 k=1,截距 b=1 的直线经过它。
- 对于 b ,该特殊点含义是,原空间中,有个 斜率为 k=1,截距 b=1 的直线经过它。
- 对于 c ,该特殊点含义是,原空间中,有个 斜率为 k=1,截距 b=1 的直线经过它。
换句话说,原空间里有一条直线经过了这三点。即 Fig.5 (a) 中的红色线。
至此,我们达到了目的。即三点在一条线上。且该线的斜率为1,截距为1。也即图fig.5(b)中参数空间的红色交点。
2.3 总结
所以对于直线检测,我们只需对每个点进行参数空间的直线变换,然后查看参数空间的交点情况。
如果没有交点,就是不共线。如果有 N 个直线交于一点,对应原空间里就是 N 个点共线。我们可以把 N 称作叠加度,或者说 参数空间中该点的亮度(名字乱起的)。亮度越高,共线的点越多,在原图中能直接观察到直线的可能性越大。
有意思的一点是,原空间两个点对应到参数空间会怎样?毕竟原空间中两点必共线,那参数空间是否必相交?参数空间里仅有两条线,且平行,对应原空间的两点是什么情况?
2.4 提升
2.4.1 实际问题
有了以上思路,就可以用 Hough 直线检测来解决实际问题了。
Hough 直线检测一般用于二值图中的直线检测,通常是一张图经过边缘算子后,检测边缘二值图是否存在直线。
如,利用 Hough 直线检测,检测 Lena 图中存在的直线。
2.4.2 求解思路
如果没有参考其他已有代码,而是基于上述一些知识,自己实现编程可能会遇到一些问题(比如我就是)。
即,如果我用 k,b 当参数空间,我可以很容易得到经过一点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),变换到参数空间里的直线为
b = − x 0 ∗ k + y 0 b = -x_0* k+ y_0 b=−x0∗k+y0
但问题是,k 可以取无穷大,b 也是,毕竟是条直线。我怎么编程表示出这条直线,因为后续还要计算各点对应线的交点,叠加度。直线无法表示出,怎么求交点?
有一种思路是解方程,考虑所有点变换到参数空间后的线方程,即
{ b = − x 0 ∗ k + y 0 b = − x 1 ∗ k + y 1 ⋮ b = − x n ∗ k + y n \left\{ \begin{matrix} \begin{aligned} b &= -x_0*k + y_0 \\ b &= -x_1*k + y_1\\ &\vdots \\ b &= -x_n*k + y_n \end{aligned} \end{matrix} \right. ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧bbb=−x0∗k+y0=−x1∗k+y1⋮=−xn∗k+yn
问题转化为,得到一组组解(k,b),该解满足的方程数即为交点叠加度(或亮度)。具体解法,先将方程转化为参数矩阵,利用矩阵,然后慢慢折腾吧。(这是遇到问题后自己想到的,可行与否,未知,且不探究。感觉可行,实在不济,两两方程求解,把解带入其他方程验证。但计算复杂度可能会特别特别高。)
第二种思路就是使用之前提到的有取值范围的 d , θ d,\theta d,θ 参数。 即 原点到直线距离 d 和 直线的法向量倾角 θ \theta θ 。好处是,它俩都是有范围的。其中 d ∈ [ − x 0 2 + y 0 2 , x 0 2 + y 0 2 ] d\in[-\sqrt{x_0^2+y_0^2},\sqrt{x_0^2+y_0^2}] d∈[−x02+y02,x02+y02] , θ ∈ [ 0 , 2 π ] \theta \in[0,2\pi] θ∈[0,2π] 。这似乎就可以用编程来实现了。
-
前面已经推导出了,过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) ,变换到参数空间 d , θ d,\theta d,θ 后的曲线方程,即
d = x 0 cos θ + y 0 sin θ d = x_0\cos\theta + y_0\sin\theta d=x0cosθ+y0sinθ
或者
d = x 0 + y 0 s i n ( θ + ψ ) , 其 中 ψ = arctan ( x 0 y 0 ) d = \sqrt {x_0+y_0}sin(\theta+\psi)\ ,其中\psi=\arctan(\frac{x_0}{y_0}) d=x0+y0sin(θ+ψ) ,其中ψ=arctan(y0x0)
编程实现如下:def getLine(x0,y0,angs_resolution= 100): """ x0: 原空间下点横坐标 y0: 原空间下点纵坐标 angs_resolution: \theta 划分精度 功能:原空间(x0,y0)点,变换到 d, \theta 参数空间的曲线。 说明:因为计算机存储是离散值,所以只是 \theta 取到一些值下的直线。当然,\theta 取值越多,越精细。 """ angs = np.linspace(0, 2*np.pi, angs_resolution) # 定义\theta 取到的离散值 d = x0 * np.cos(angs) + y0 * np.sin(angs) return angs,d测试一下,点 (x0, y0) 设为 (1, 1),运行程序,可以得到如下结果

原空间中一点,对应到 θ , d \theta,d θ,d 参数空间是一条正弦线。
-
求原空间所有点对应的正弦线,计算亮度
事实上,
getLine()输出的是一系列离散点,点横坐标是 θ \theta θ ,纵坐标是 d。我们查找所有输出值中 ( θ , d ) (\theta,d) (θ,d) 重复次数就行了。重复次数,就是亮度。而且还有一点方便的是,对于每组getLine()输出值, θ \theta θ 都是相同的,因此我们只需检查每组对应位 d 是否相同(或小于某一阈值)即可。
2.4.3 自编程实现
完整代码:
import numpy as np
import matplotlib.pyplot as plt
import cv2
def getLine(x0,y0,angs_resolution= 100):
"""
x0: 原空间下点横坐标
y0: 原空间下点纵坐标
angs_resolution: \theta 划分精度
功能:原空间(x0,y0)点,变换到 d, \theta 参数空间的曲线。
说明:因为计算机存储是离散值,所以只是 \theta 取到一些值下的直线。当然,\theta 取值越多,越精细。
"""
angs = np.linspace(0, 2*np.pi, angs_resolution) # 定义\theta 取到的离散值
d = x0 * np.cos(angs) + y0 * np.sin(angs)
return angs,d
def Hough(edgeImg, angsDiv = 500, dDiv=1000):
# 获取图像尺寸
ySize, xSize = edgeImg.shape
# 得到二值图中所有点坐标(x,y)
y, x = np.where(edgeImg != 0)
# 大致确定 d 范围
dMax = np.sqrt(np.max(y)**2+np.max(x)**2)
# 分辨率
d_res = 2*dMax/(dDiv-1)
ang_res = 2*np.pi/(angsDiv-1)
# 亮度模板,起初为全黑,当经过某点,亮度 +1
template = np.zeros((dDiv, angsDiv), dtype = np.uint8)
# 亮度叠加计算
for xx in range(len(x)):
_, _d = getLine(x[xx], y[xx], angsDiv)
_n = ((_d+dMax)/d_res).astype(np.int64)
angle = np.arange(0, angsDiv)
for p in zip(angle, _n):
template[p[1], p[0]] = template[p[1], p[0]] + 1
return template
if __name__ == "__main__":
# 读取图片
imgPath = "C:\\Users\\zhangwei156\\Desktop\\figure\\lena.bmp"
grayImg = cv2.imread(imgPath, 0)
# 提取边缘
edgeImg = cv2.Canny(grayImg, 300, 500)
# 设置离散的精度
angsDiv = 500
dDiv = 1000
# 霍夫变换
forceImg = Hough(edgeImg, angsDiv, dDiv)
plt.imshow(edgeImg)
plt.show()
plt.imshow(forceImg)
plt.show()
结果如下:
# 一些后面要用到的常数
y, x = np.where(edgeImg != 0)
dMax = np.sqrt(np.max(y)**2+np.max(x)**2)
d_res = 2*dMax/(dDiv-1)
ang_res = 2*np.pi/(angsDiv-1)
# 这是只考察了最大点,即亮度最大的点
ind = np.where(forceImg == np.max(forceImg))
# theta 和 d 的真实值
theta = (ind[1])* ang_res
d = -dMax + (ind[0]) * d_res
# 对应原空间的直线
xx = np.arange(512)
i = 0
yy = (d[i] - xx*np.cos(theta[i]))/np.sin(theta[i])
plt.plot(xx, yy, "r", linewidth = 0.3)
plt.imshow(edgeImg)
plt.show()
结果:
说明:
- 为了编程方便,同时能形象展示亮度信息,我把角度 θ ∈ [ 0 , 2 π ] \theta\in[0, 2\pi] θ∈[0,2π] 和距离 d ∈ [ − d M a x , d M a x ] d\in[-dMax,dMax] d∈[−dMax,dMax] 范围各自等分了共 a n g s D i v angsDiv angsDiv 份 和 d D i v dDiv dDiv 份。 f o r c e I m g forceImg forceImg 图像横纵轴坐标表示的是第几份(全是整数),不是直接的 θ \theta θ 和 d。如果求解真正的值,对于 d = − d M a x + y ∗ d M a x − ( − d M a x ) d D i v − 1 d = -dMax + y * \frac{dMax - (-dMax)}{dDiv-1} d=−dMax+y∗dDiv−1dMax−(−dMax); θ \theta θ 同理。
- 对于如上自编程的实现,分辨率 angsDiv, dDiv 设置真的很重要,设置过小的话。结果可能看起来好像不对,就是精度问题。况且里面还用到了许多四舍五入。
- 分辨率越大,计算效率越低。已经感受到了Hough变换耗时的地方。不过,一些库(如openCV)里应该会有精巧方法,对此有所优化。
- 一个可供改进的点:可以考虑将 θ , d \theta,d θ,d 相近的划归到一条直线,通过设定阈值实现,这样结果会更合理。
- 上面只使用了亮度最大的点,即只考虑原图中最直线的一条直线。
- 还有另一种编程思路,即借助另一种变换实现。即 Radon 变换。
2.5 openCV对应代码解读
先省略之,有空再读。基本原理清楚了,应该很好理解源码。
文档书写有些卡顿
霍夫圆检测另起一篇:详解 Hough 变换(下)圆形检测
以及Hough 直线检测的拓展:Radon 变换原理与应用