2021电工杯数学建模B题代码与思路(Python)
题目内容
国家《第十四个五年规划和 2035 年远景目标纲要》中提出,将 2030 年实现
“碳达峰”与 2060 年实现“碳中和”作为我国应对全球气候变暖的一个重要远景目标。光伏建筑一体化(BIPV)是充分利用工业建筑、公共建筑屋顶等资源实施分布式光伏发电工程,它对我国实现“碳达峰”和“碳中和”起到重要作用。目前已有北京、天津、上海、重庆、内蒙古、浙江等 31 地发布光伏建筑一体化未来三至五年相关政策,这将对光伏建筑一体化相关上市企业的发展带来一定影响。
在股票交易软件中,每支股票都有日 K 线(由开盘价、收盘线、最高价、最
低价构成),还有移动平均线(5 日、10 日、20 日等),通过对日 K 线和移动平均线的分析,可知每支股票的走势。股票市场中有板块指数(将同一板块的个 股按不同的权重方式生成相关指数),它是对该板块走势的整体反映。
现统计沪深股市中 37 家光伏建筑一体化相关企业的股票数据(见附件 1),
将这 37 家企业股票看作一个整体称为光伏建筑一体化板块。光伏建筑一体化板块作为新兴板块,通过对板块指数发展趋势做出预测,可以了解板块相应行业未来的发展趋势。 请根据所给数据资料,解决以下问题:
1.利用附件 1 中数据,给出光伏建筑一体化板块指数的移动平均线(5 日、
10 日、20 日等)模型,并绘制 2019 年 4 月 1 日至 2021 年 4 月 30 日该板块指数的移动平均线。
2.利用 2021 年 5 月 6 日至 5 月 28 日数据,对所建立模型进行误差分析并修 正模型,根据修正后的模型对该板块未来发展趋势做出预测,给出 5 月 28 日后20 个交易日的日移动平均线、3 周的周移动平均线、2 个月的月移动平均线。
3.利用 2019 年 4 月 1 日至 2021 年 5 月 28 日数据,以 2 个月为一个时间段,对上证指数和光伏建筑一体化板块指数进行相关性分析。
4.对光伏建筑一体化板块个股投资风险进行评估,给出该板块 37 支股票
2021 年 6 月份投资风险由低到高的排序结果。假定投资者持有资金 100 万元人民币,欲全部用于该板块的投资,请给出 2021 年 6 月份的最优投资方案(当日可用于投资的资金为上一个交易日结束后投资者所持有的资金,且每日持股数不超过 5 支)。
5.请给相关部门写一份不少于 1500 字关于我国光伏建筑一体化行业未来发
展趋势的报告。
第一问
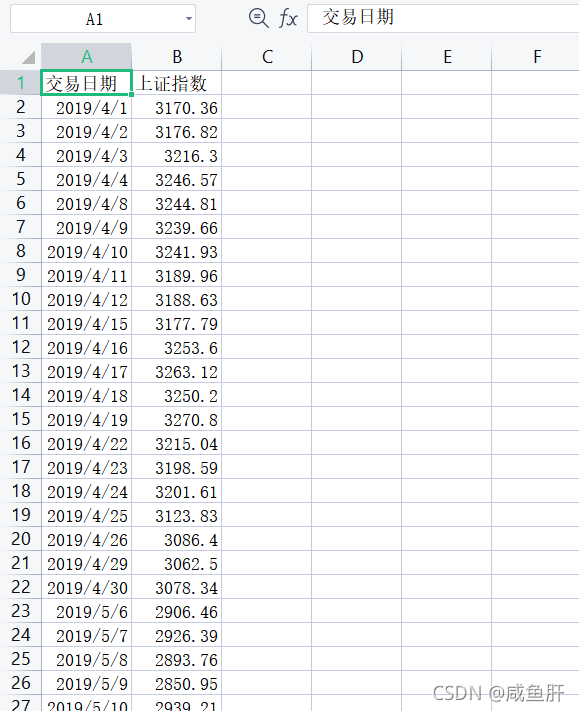
首先是读取数据,要注意的是,附件一的excel表格有多个sheet。

所以要在pandas读取的时候加一个None即可,这个其实是sheet_name的参数。
#读取数据
import pandas as pd
import numpy as np
data_path = "F:/train/建模比赛/2021电工杯/B题/附件1.xlsx"#路径
data = pd.read_excel(data_path,None)
sheet_name_list = [i for i in data]#读取sheet_name,后面会用
写一个new_time()函数,用来查看一下,各个公司的上市时间。
def new_time(x):#查看最新上市时间
s = []
p = []
for i in sheet_name_list:
s.append(x[i]["交易时间"][0])#具体时间
p.append(i)#时间所在的sheet_name
return [s,p]#返回一个列表
s = new_time(data)#调用
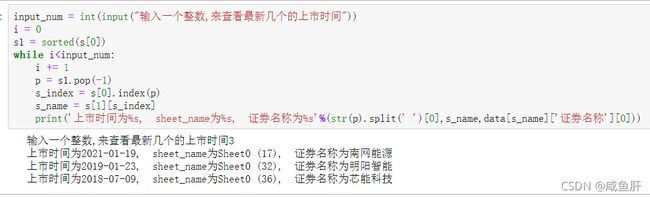
再写一个把他们上市时间排序的程序。
input_num = int(input("输入一个整数,来查看最新几个的上市时间"))
i = 0
s1 = sorted(s[0])
while i<input_num:
i += 1
p = s1.pop(-1)
s_index = s[0].index(p)
s_name = s[1][s_index]
print('上市时间为%s, sheet_name为%s, 证券名称为%s'%(str(p).split(' ')[0],s_name,data[s_name]['证券名称'][0]))
结果:
接下来就是计算他们的板块指数了。题目中有说要按他们的各个权重来计算板块指数,我这里选用的是成交量和收盘价来计算,以各股每天的成交量比上总成交量作为权重,在写出如下式子即可。

基准日市值的计算,我选择了第一家在该板块上市公司的第一天作为基准日。
def base_date_sum(x):#计算基准日市值
base_price = []#基准日开盘价
base_money = []#基准日成交量
for i in range(37):
if i == 0:
datatime = pd.to_datetime(x[sheet_name_list[i]]["交易时间"].values)
restock = x[sheet_name_list[i]].set_index(datatime)
p = restock["1992-03-01":"2021-04-30"]["成交量"][0]
p1 = restock["1992-03-01":"2021-04-30"]["收盘价"][0]
base_price.append(p1)
base_money.append(p)
else:
pass
weight = base_money/sum(base_money)#基准日权重
money = sum(base_price*weight)
return money
base_sum = base_date_sum(data)#基准日市值
base_sum
这样就有基准日的市值了,此外我还统计了一下,各个公司2019-03-01到2021-04-30的上市天数
def len_index(x):#各个公司2019-03-01到2021-04-30的上市天数
p = []
for i in sheet_name_list:
datatime = pd.to_datetime(x[i]["交易时间"].values)
restock = x[i].set_index(datatime)
p.append([str(len(restock["2019-03-01":"2021-04-30"])),str(i)])
return p
len_index(data)
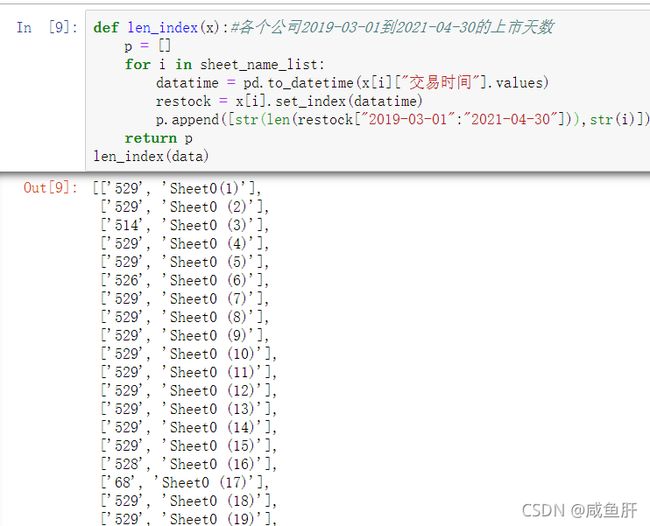
除了新上市的公司天数很少以外,还有不一样的。
有了基准日市值之后就要计算板块指数了,要保证在同一天,所以我选择了把表拼接起来。
#拼接表
for i in range(1,37):
if i == 1:
data1 = pd.concat([data[sheet_name_list[0]],data[sheet_name_list[1]]])
else:
data1 = pd.concat([data1,data[sheet_name_list[i]]])
data1.head()
[len(data[i].columns) for i in sheet_name_list]#各个表的列的数量
运行之后果然是不一样的,有的是11,有的是13,这个缺失值没什么影响。
datatime = pd.to_datetime(data1["交易时间"].values)
restock = data1.set_index(datatime)
restock1 = restock["2019-03-05":]
k_list = []#查看一下整表的长度,把他们的索引值记录下来。
k = [str(i).split(' ')[0] for i in restock1.index]
for i in k:
if i not in k_list:
k_list.append(i)
len(k_list)
#运行结果为543
接下来就是计算板块指数了。
#计算板块指数
num_list = []#储存板块指数
for i in k_list:
#先计算权重
w = np.array([j for j in restock1[i:i]["成交量"]])
weight = w/sum(w)
#计算市值
m = np.array([j for j in restock1[i:i]["收盘价"]])
money = sum(m*weight/len(weight))
#计算板块指数
sector_index = money/base_sum*1000
num_list.append(sector_index)
计算之后再可视化一下
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,6))
plt.plot(num_list,'r')
c = [0,100,200,300,400,500]
plt.xticks(c,[str(restock1.index[i]).split(' ')[0] for i in c])
结果
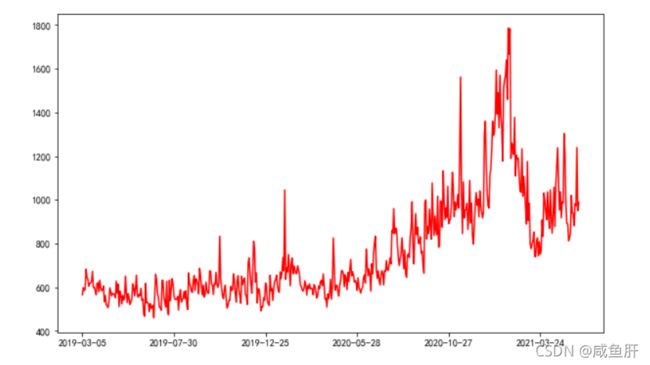
计算完事再新建数据集,把得到的数据存到数据集里,还记得data1是拼接来的吗,pandas拼接,我这里用的是纵向拼接,就是像搭积木一样,所以导致了len(restock1.index)#结果为19602
所以清洗一下,去个重。再写入创建的数据集中。
time_list = []
for i in restock1.index:
if i not in time_list:
time_list.append(i)
df = pd.DataFrame()
df['时间'] = time_list
df['板块指数'] = num_list
题目中还要求了5日,10日和20日的移动平均线,使用pandas的rolling函数,移动窗口函数。
num5_list = df['板块指数'].rolling(window=5)
num10_list = df['板块指数'].rolling(window=10)
num20_list = df['板块指数'].rolling(window=20)
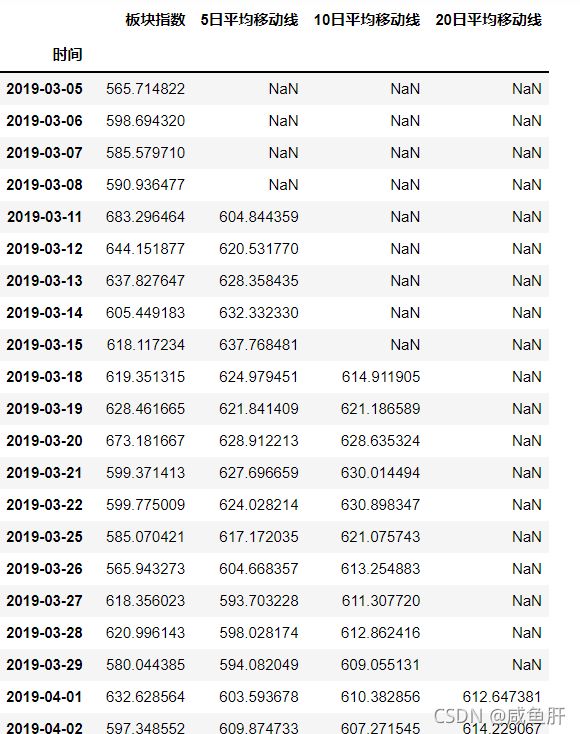
df['5日平均移动线'] = num5_list.mean()
df['10日平均移动线'] = num10_list.mean()
df['20日平均移动线'] = num20_list.mean()
df
from pyecharts.charts import Line
from pyecharts import options as opts
line = (Line()
.add_xaxis([str(i).split(' ')[0] for i in df['时间']])
.add_yaxis("5日平均移动线",[i for i in df['5日平均移动线']])
.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
.add_xaxis([str(i).split(' ')[0] for i in df['时间']])
.add_yaxis("10日平均移动线",[i for i in df['10日平均移动线']])
.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
.add_xaxis([str(i).split(' ')[0] for i in df['时间']])
.add_yaxis("20日平均移动线",[i for i in df['20日平均移动线']])
.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
)
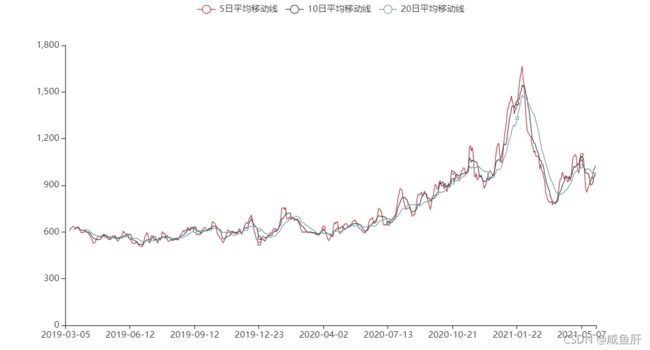
line.render_notebook()
第二问
第二问简单来说就是预测。
ARIMA模型
ARIMA的难点在于确定p,d,q的值。使用这个模型的数据,一定要的是平稳的,但是哪有那么多平稳的数据,所以使用的时候就要做差分,一阶至多阶直到数据变得平稳,做了几阶,就是d的值。而p,q的值要做自相关(ACF)和偏自相关图(PACF)来确定。具体看这里
我做了一阶差分,数据差不多就平稳了。因为不是每天都有数据的,所以重采样的时候,也就是下面第二句代码,会包含空值,所以一定要记得去重,我就是因为没去重弄了半天一直都像下面这样,还傻乎乎跑去问老师。

df = df.set_index('时间')
a = df['板块指数'].resample('B').mean()
# a = df['板块指数']
a1 = a["2021-05-06":]
plt.figure(figsize=(10,6))
a.plot()
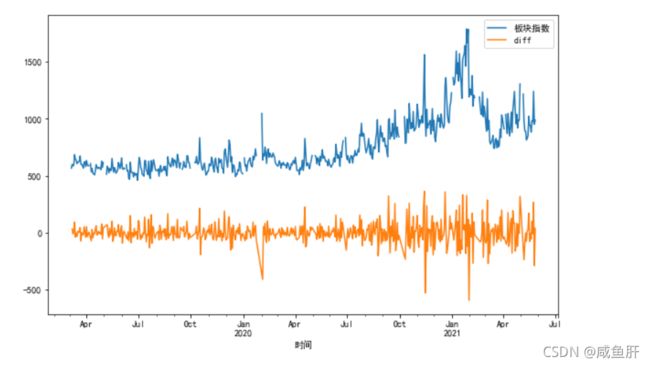
diff = a.diff().dropna()
diff.plot(label='diff')
plt.legend()
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
acf_diff = plot_acf(diff,lags=30)
plt.title('ACF')
plt.show()
pacf_diff = plot_pacf(diff,lags=30)
plt.title('PACF')
plt.show()

这里我选的q为1,p为4,如果不知道怎么确定p,q的值的话可以看看这个文章。
接下来就是用他来预测了
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(a,order=(1,1,4))
arima_result = model.fit()
print(arima_result.summary())#打印ARIMA的指标
#预测
pred_vals = arima_result.predict(start=543,end=563,
dynamic=True, typ='levels')
print(pred_vals)
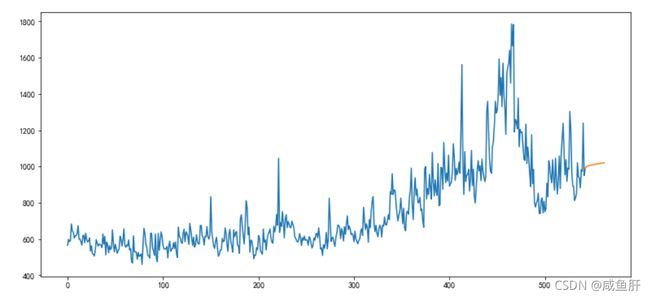
plt.figure(figsize=(13,6))
plt.plot(num_list)
plt.plot(pred_vals)
plt.plot(np.array(pred_vals))
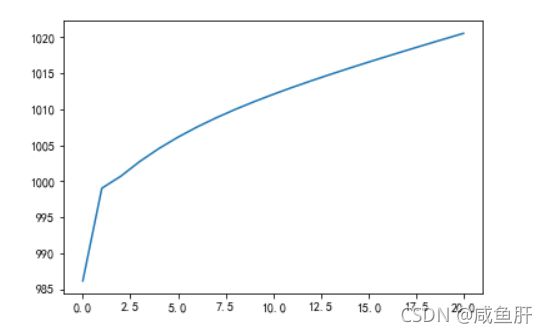
很像一个直线,应该是动态预测与静态预测的问题。变量预测过程分为动态预测与静态预测.动态预测中预测样本的初始值使用滞后变量 Y 的实际值,在随后的预测中使用 Y 的预测值,动态预测在预测过程中重复使用滞后因变量的预测值 。参考
LSTM
说到LSTM就得提一下RNN。从下图是循环神经网络的结构。(可点击链接了解RNN)
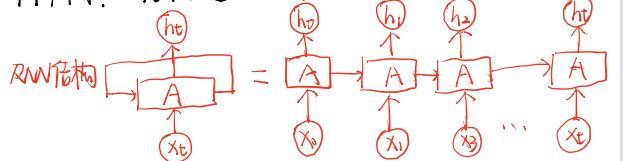
但是RNN有长期依赖问题,而LSTM就是通过刻意的设计来避免长期依赖问题。结构如下

简单来说就是LSTM作为RNN的变种,其核心的地方再于:
1.提出了门机制:遗忘门、输入门、输出门;
2.细胞状态:在RNN中只有隐藏状态的传播,而在LSTM中,引入了细胞状态。
具体可见链接:链接1,链接2
LSTM模型将学习将过去的观测序列作为输入映射到输出观测的函数。说人话就是拿前多少天的数据作为输入,这里的多少天称为步长,输出就是下一天的数据。
def split_sequence(sequence, n_steps):
X, y = list(), list()
for i in range(len(sequence)):
end_ix = i + n_steps
if end_ix > len(sequence)-1:
break
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
其中的n_steps就是步长。接下来就是reshape他们的维度
data2,labels = split_sequence(df['板块指数'],10)
data3 = data2.reshape((len(data2),10,1))
搭建LSTM神经网络模型
如果对下列代码中LSTM()的参数有不理解的地方,点击这里了解
from keras.models import Sequential
from keras.layers import LSTM,Dropout,Dense
model = Sequential()
model.add(LSTM(20,activation="relu",input_shape=(10,1),return_sequences=True))
model.add(LSTM(30,activation="relu",return_sequences=True))
model.add(LSTM(30,activation="relu"))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
model.summary()
训练
如果对下列代码中fit()的参数有不理解的地方,请点击这里
history = model.fit(data3,labels,epochs=20,batch_size=20,validation_split=0.2)
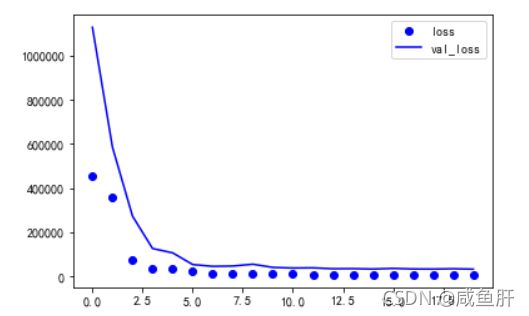
画一下loss曲线
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(range(20),loss,"bo",label="loss")
plt.plot(range(20),val_loss,"b",label='val_loss')
plt.legend()
plt.show()
#定义方法,可以预测2021-5-28后20日的结果
def predict_20days(samples):
results = []
for i in range(20):
result = model.predict(samples[-1].reshape(1,10,1))
results.append(result)
sample = np.append(samples[-1][1:],result)
sample = sample.reshape((1,10,1))
samples = np.concatenate((samples,sample),axis=0)
return results
results = predict_20days(data3)#预测
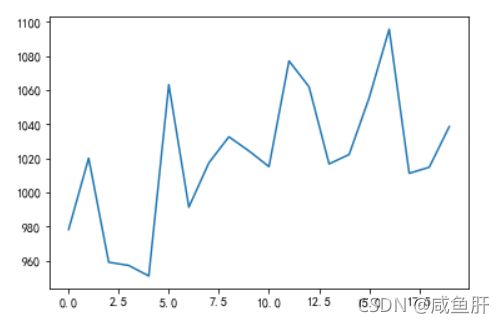
可视化
plt.plot(range(len(df)),df['板块指数'])
plt.plot(range(len(df),len(df)+20),np.array(results).reshape(20,))
plt.plot(np.array(results).reshape(20,))
第三问
数据的获取:Ajax爬取
动态加载的数据不在你访问的url里面,这时候就需要你找到数据所在的url。点击F12,再点击Network,之后刷新页面,按下CTRL+F,寻找你要的数据,我这里找的就是2017-09-21。
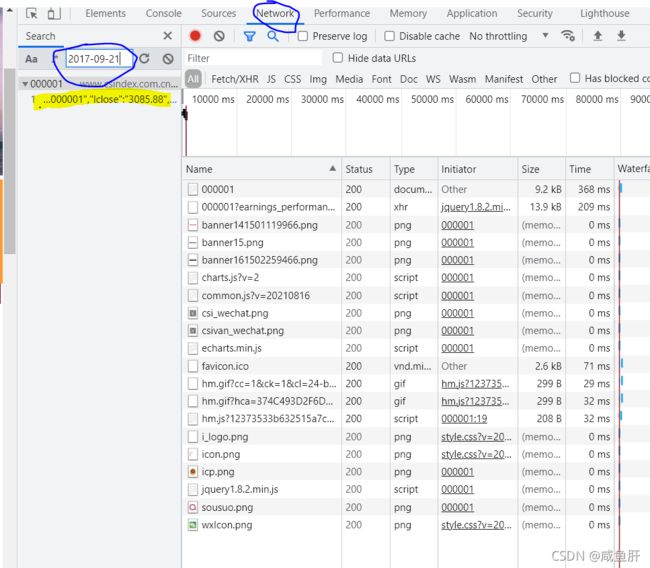
很明显,黄色部分就是我们要的数据的所在位置,点击他。

数据在红色线条位置,点击Headers,使用红色部分圈出来的参数作为我们伪装请求的headers。
import requests
from lxml import etree
import re
Ajax_url = 'http://www.csindex.com.cn/zh-CN/indices/index-detail/000001?earnings_performance=5%E5%B9%B4&data_type=json'
headers = {
'Accept': 'application/json, text/javascript, */*; q=0.01',
'Accept-Encoding': 'gzip, deflate',
'Accept-Language': 'zh-CN,zh;q=0.9',
'Connection': 'keep-alive',
'Cookie': 'Hm_lvt_12373533b632515a7c0ccd65e7fc5835=1629794920; Hm_lpvt_12373533b632515a7c0ccd65e7fc5835=1629797891',
'Host' : 'www.csindex.com.cn',
'Referer': 'http://www.csindex.com.cn/zh-CN/indices/index-detail/000001',
'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/92.0.4515.159 Safari/537.36',
'X-Requested-With': 'XMLHttpRequest'
}
res = requests.get(url=Ajax_url,headers=headers)
s = res.text
s
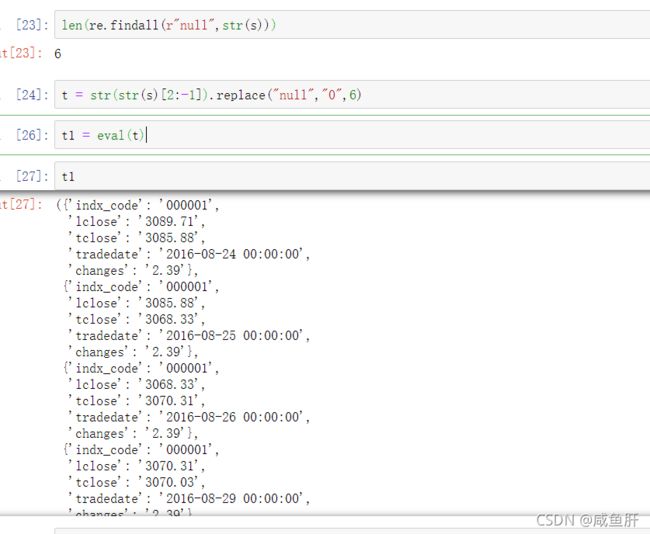
len(re.findall(r"null",str(s)))#结果为6
t = str(str(s)[2:-1]).replace("null","0",6)
t1 = eval(t)
t1
#明确要的范围是2019 年 4 月 1 日至 2021 年 5 月 28 日
#所以先找出来相应的索引,在取值,有点啰嗦,但是对别人可能更容易理解一点
for i in range(len(t1)):
if t1[i]['tradedate'] == '2019-04-01 00:00:00':
s1 = i
elif t1[i]['tradedate'] == '2021-05-28 00:00:00':
s2 = i
print(s1,s2)#结果为629 1153
保存为csv格式
#指数看收盘价就行了
tclose = []
time = []
for i in t1[s1:s2+1]:#左闭右开,所以加一
p = i['tradedate'].split(' ')[0]
time.append(p)
tclose.append(i['tclose'])
import pandas as pd
df = pd.DataFrame()
df['交易日期'] = time
df['上证指数'] = tclose
df.to_csv('上证指数爬取数据.csv',encoding='utf-8',index=False)
皮尔逊相关系数
#读取爬取到的上证指数数据
s = open('./上证指数爬取数据.csv',encoding='utf-8')
Shanghai_Stock_Index_data = pd.read_csv(s)
s.close()
Shanghai_Stock_Index_data.head()
Shanghai_Stock_Index_data = Shanghai_Stock_Index_data.set_index('交易日期')
Shanghai_Stock_Index_data.index = pd.to_datetime(Shanghai_Stock_Index_data.index)
a = Shanghai_Stock_Index_data['上证指数'].resample('M').mean()
len(a)#结果是26
df.index = pd.to_datetime(df.index)
a1 = df['板块指数'].resample('M').mean()
len(a1)#结果是27,多取了一个
a1 = a1[1:]
可视化一下
from pyecharts.charts import Line
from pyecharts import options as opts
line1 = (Line()
.add_xaxis(a.index.tolist())
.add_yaxis("板块指数",a.values)
.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
.add_xaxis(a.index.tolist())
.add_yaxis("上证指数",a1.values)
.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
)
line1.render_notebook()

计算两组数据的相关性,一般采用相关系数来描述两组数据的相关性,而相关系数则是由协方差除以两个变量的标准差而得,相关系数的取值会在 [-1, 1] 之间,-1 表示完全负相关,1 反之。
协方差
![]()
相关系数
![]()
手写版
def mean(x):
return sum(x) / len(x)
# 计算每一项数据与均值的差
def de_mean(x):
x_bar = mean(x)
return [x_i - x_bar for x_i in x]
# 辅助计算函数 dot product 、sum_of_squares
def dot(v, w):
return sum(v_i * w_i for v_i, w_i in zip(v, w))
def sum_of_squares(v):
return dot(v, v)
# 方差
def variance(x):
n = len(x)
deviations = de_mean(x)
return sum_of_squares(deviations) / (n - 1)
# 标准差
import math
def standard_deviation(x):
return math.sqrt(variance(x))
# 协方差
def covariance_true(x, y):
n = len(x)
return dot(de_mean(x), de_mean(y)) / (n -1)
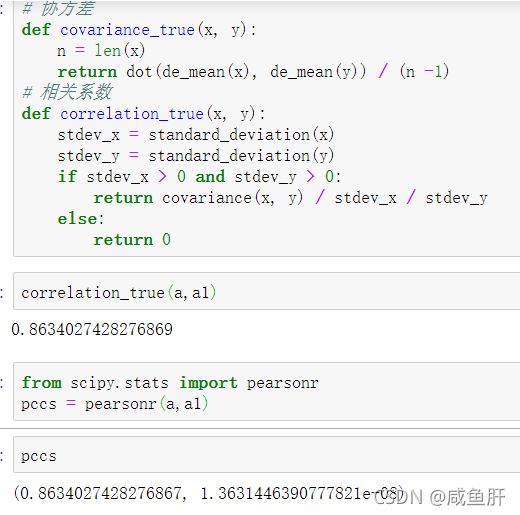
# 相关系数
def correlation_true(x, y):
stdev_x = standard_deviation(x)
stdev_y = standard_deviation(y)
if stdev_x > 0 and stdev_y > 0:
return covariance(x, y) / stdev_x / stdev_y
else:
return 0
调用
correlation_true(a,a1)
调包版
from scipy.stats import pearsonr
pccs = pearsonr(a,a1)
pccs
余弦相似度
直接掉包吧还是
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(np.array(a).reshape(1,-1),np.array(a1).reshape(1,-1))
#如果不reshape,会如下报错
#Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.
#reshape(1, -1) if it contains a single sample.
#使用数组重塑数据。如果数据具有单个特征或数组,则重塑(-1,1)。如果数据包含单个样本,则重塑(1,-1)。
第四问
我选择了历史模拟法计算VaR值,如果对别的方法有兴趣可以点这里
先计算日收益率,因为我这里没用买入卖出的数据,所以仅在这里日收益率就和涨跌幅相当,其实我不懂股票看了一下午的晦涩难懂的词汇,如果有误,欢迎指正。
写了一个在置信度为95%的时候的VaR值计算
def var_5_num(name):
VaR_5_list = []
name_list = []
for i in name:
data_time = data[i].set_index('交易时间')
data_time = data_time['2021-04':]
data_time['日收益率'] = data_time['收盘价'].pct_change()
VaR_5 = np.percentile(data_time['日收益率'].dropna(), 5)
VaR_5_list.append(VaR_5)
name_list.append(data[i]['证券名称'][0])
return [VaR_5_list,name_list]
在由得到的VaR值来排序,比较风险值的大小,
var_true = var_5_num(sheet_name_list)#调用函数,得到各股的VaR值
用来排序的函数
def var_sort(x,num):
s = x[0]
p = [i for i in zip(s,x[1])]
s_sort = sorted(s)
s_index = [s.index(i) for i in s_sort]
# for i in s_sort:
# s_index.append(s.index(i))
p_sort = [p[i] for i in s_index[:num:]]
return p_sort
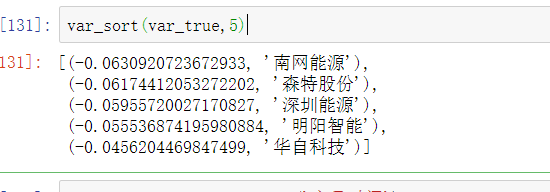
这个函数里的num可以自己定只要不超过股票的个数就行,输入5,就代表查看风险最低的前5只股票。
var_sort(var_true,5)
data1_2 = data1.set_index('交易时间')
p2 = data1_2.loc[data1_2['证券名称']=='启迪设计']['收盘价'].pct_change().dropna()
VaR_5 = np.percentile(p2, 5)
VaR_1 = np.percentile(p2, 1)
plt.figure(figsize=(10,8),dpi=70)
plt.hist(p2,bins=100,color='b',alpha=0.6)
plt.plot([VaR_1,VaR_1],[0,90],color='y',label='VaR_1')
plt.plot([VaR_5,VaR_5],[0,90],color='r',label='VaR_5')
plt.legend()
plt.title('启迪设计的日收益率分布')

至于投资什么的,我完全不懂,我只能看着自己算出来的VaR值最小的5个股票来投资,加仓什么的都不知道。我就梭哈这前五个股票,等权重投资,各占20%。
第五问
就从这个板块的出发点考虑,节能环保,还有国家政策,人民对其认识程度什么的方面考虑吧。