算法刷题记录(Day 62)

权限查询(csp-201606-3)

原题链接

解题思路:以权限为主体，建立不同权限或者不同等级的权限的访问角色表。若角色role有privilege:level的权限，则role应该被添加到privilege的0到level的数组中。同时，为了方便，需要维护一个数组，记录每一个角色对于每一个权限所拥有的最大的等级。
在进行判断中，对于是否具有权限的判断，仅需判断权限的访问角色表中的角色是否和用户的角色有交集；对于最高权限的判断，遍历用户的所有角色，利用角色-最大权限等级矩阵进行获取。

问题是:
如何去返回具有的最高等级呢？->从本身的最高等级查起
如何去标识->查询0等级和查询最高等级之间的区别->使用p来进行
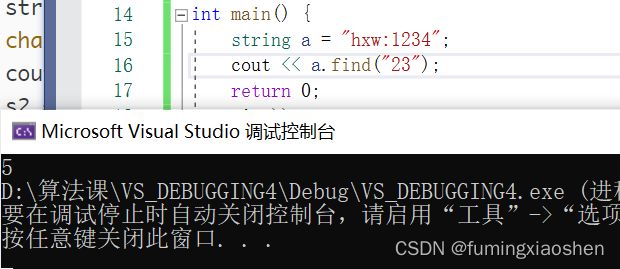
map和vector的无法嵌套使用->string的find来进行代替

#include
#include
#include
#include
using namespace std;
#define UMAX 110
int p, r, u, q;
char c;
string cur1, cur11, cur12;
int cur2,cur3;//cur3用于查询最高等级还是是否是该等级
struct privilege {
	string p2r[UMAX];//权限等级0-9
	int mp=0;//代表最高权限
}P[UMAX];
map<string, int> p2n;
map<string, int >u2n;
map<string, int> r2n;
string u2r[UMAX][UMAX];
//对于每一种角色需要存储其具有的最高权限
int rmaxp[UMAX][UMAX];
void pri_process() {
	cin >> cur1;
	int p = cur1.find(":");
	if (p < 10000 && p >= 0) {
		cur11 = cur1.substr(0, p);
		cur12 = cur1.substr(p + 1);
		cur2 = stoi(cur12);
		cur3 = 0;
	}
	else {
		cur11 = cur1;
		cur2 = 0;
		cur3 = 1;
	}
}
int main() {
	memset(rmaxp, -1, sizeof(rmaxp));
	cin >> p;
	for (int i = 1; i <= p; i++) {
		//cin >> cur1;
		pri_process();
		//cout << cur11 << " " << cur2 << endl;
;		p2n[cur11] = i;
		P[i].mp = cur2;
	}
	cin >> r;
	for (int i = 0; i < r; i++) {
		string rname;
		int num;
		cin >> rname;
		r2n[rname] = i;
		cin >> num;
		for (int j = 0; j < num; j++) {
			//cin >> cur1;
			pri_process();
			//cout << cur11 << " " << cur2 << endl;
			int p = p2n[cur11];
			if(cur2> rmaxp[i][p])rmaxp[i][p] = cur2;//角色所具有的最大的权限值
			for (int i = 0; i <= cur2; i++) {
				P[p].p2r[i] += (" " + rname + " ");
			}
		}
	}
	
	/*for (int i = 1; i <= p; i++) {
		cout << endl << endl;
		for (int j = 0; j <= P[i].mp; j++) {
			cout << P[i].p2r[j] << endl;
		}
	}*/
	cin >> u;
	for (int i = 1; i <= u; i++) {
		string uname;
		cin >> uname;
		int num;
		cin >> num;
		u2n[uname] = i;
		for (int j = 0; j < num; j++) {
			string role;
			cin >> role;
			u2r[i][j]=role;
		}
	}
	
	cin >> q;
	for (int i = 0; i < q; i++) {
		string uname;
		int pnum, unum;
		int level;
		cin >> uname;
		pri_process();
		pnum = p2n[cur11];
		unum = u2n[uname];
		if (!pnum || !unum) {
			cout << "false" << endl;
			continue;
		}
		level = cur2;
		if (!cur3 || P[pnum].mp==0) {
			int res = 0;
			for (int j = 0; u2r[unum][j] != ""; j++) {
				int judge = (P[pnum].p2r[cur2]).find(u2r[unum][j]);
				if (judge > 0 && judge <30000) {
					res = 1;
					break;
				}
			}
			if (res) cout << "true" << endl;
			else cout << "false" << endl;
		}
		else {
			int res = -1;
			for (int j = 0; u2r[unum][j] != ""; j++) {
				int rnum = r2n[u2r[unum][j]];
				if (rmaxp[rnum][pnum] > res) res = rmaxp[rnum][pnum];
			}
			if (res == -1) cout << "false" << endl;
			else cout << res << endl;
		}

	}

}

tip:
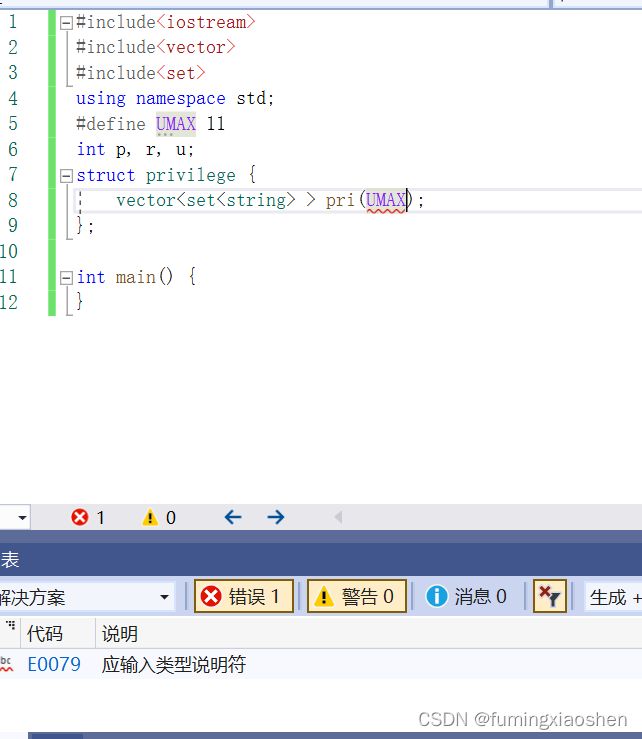
1.运行错误代表的是出现了诸如溢出之类的问题

2.调试过程中的输出不要忘记注释掉。
3.vector里面嵌套map等stl容器可能会存在错误

4.string的find返回的是子串开始的位置

5.map当不存在时返回的是0
6.注意看清楚题目的条件！！！
7.使用string.h而不是string，否则会报编译错误

参考链接:
string find使用
csp编译错误

赤壁之战

原题链接
若 使用dp[i][j]代表到i为止长度为j的子串的个数，则时间复杂度O(MNN)，肯定会超时
那么能否仅仅计算最长的严格升序列，然后再利用组合数求得最终的结果，但是除了由最长增序列求解长度为M的个数，长度为M的也可能位于非最长增序列中

使用离散化+树状数组的方式，来将对于特定的长度、特定的位置，需要遍历前面所有的数字以求和转化为树状数组的求和过程。

在计算长度为i的过程中，B中维护的是特定位置以前的长度为i-1的前缀和，鉴于在A中，可能存在相同的，因此在遍历过程中逐步在B中加上i-1的值。

#include
#include
#include
using namespace std;
#define NMMAX 1010
//#define MOD 1000000007
const int MOD=1e9+7;
int N, M, T;
int A[NMMAX], B[NMMAX];
int dp[NMMAX][NMMAX];
int lowbit(int x) {
	return x & (-x);
}
int ask(int x) {
	int res = 0;
	for (int i = x; i; i -= lowbit(i)){
	   //res = ((long long) (res+B[i]))%MOD;
	   res+=B[i];
	   res%=MOD;
	} 
	return res;
}
void add(int x, int inc) {
	for (int i = x; i <= N; i += lowbit(i)) {
		//B[i] = ((long long)(B[i]+inc))%MOD;
		B[i]+=inc;
		B[i]%=MOD;
	}
}
int main() {
	cin >> T;
	int c = 1;
	while (T--) {
		memset(dp, 0, sizeof(dp));
		cin >> N >> M;
		for (int i = 0; i < N; i++) {//树状数组必须从1开始
			cin >> A[i];
			B[i] = A[i];
		}
		sort(B, B + N);
		int cnt=unique(B, B + N ) - B;
		for (int i = 0; i < N; i++) {
			A[i] = lower_bound(B, B + cnt, A[i]) - B + 1;//从1开始
		}
		//由B去维护树状数组
		//int i;
		for (int i = 1; i <= M; i++) {//遍历所有的长度
			memset(B, 0, sizeof(B));
			for (int j = 0; j < N; j++) {
				if (i == 1) dp[i][j] = 1;
				else dp[i][j] = ask(A[j] - 1); //计算A[j]前面的所有的内容之和作为当前的值
				add(A[j], dp[i - 1][j]);//体现了
			}
		}
		int res = 0;
		for (int i = 0; i < N; i++) {
			res =  ((res + dp[M][i])) ;//% MOD;
			res%=MOD;
		}
		cout << "Case #" << c++ << ": ";
		cout << res << endl;
	}
}

#include
#include
#include
using namespace std;
#define NMMAX 1010
#define MOD 1000000007
//const int MOD=1e9+7;
int N, M, T;
int A[NMMAX], B[NMMAX];
int dp[NMMAX][NMMAX];
int lowbit(int x) {
	return x & (-x);
}
int ask(int x) {
	int res = 0;
	for (int i = x; i; i -= lowbit(i)){
	   res = ((long long) (res+B[i]))%MOD;
	   //res+=B[i];
	  // res%=MOD;
	} 
	return res;
}
void add(int x, int inc) {
	for (int i = x; i <= N; i += lowbit(i)) {
		B[i] = ((long long)(B[i]+inc))%MOD;
		//B[i]+=inc;
		//B[i]%=MOD;
	}
}
int main() {
	cin >> T;
	int c = 1;
	while (T--) {
		memset(dp, 0, sizeof(dp));
		cin >> N >> M;
		for (int i = 0; i < N; i++) {//树状数组必须从1开始
			cin >> A[i];
			B[i] = A[i];
		}
		sort(B, B + N);
		int cnt=unique(B, B + N ) - B;
		for (int i = 0; i < N; i++) {
			A[i] = lower_bound(B, B + cnt, A[i]) - B + 1;//从1开始
		}
		//由B去维护树状数组
		//int i;
		for (int i = 1; i <= M; i++) {
			memset(B, 0, sizeof(B));
			for (int j = 0; j < N; j++) {
				if (i == 1) dp[i][j] = 1;
				else dp[i][j] = ask(A[j] - 1);
				add(A[j], dp[i - 1][j]);
			}
		}
		int res = 0;
		for (int i = 0; i < N; i++) {
			res =  ((long long)(res + dp[M][i])) % MOD;
			//res%=MOD;
		}
		cout << "Case #" << c++ << ": ";
		cout << res << endl;
	}
}

tip:
1.在debug过程中发现关于%mod很奇怪，起初是下面的代码WA，后来又好了
2.对于求和的内容，离散化的思想很重要。同时，对于大小的比较，也可以考虑到离散化的角度。
3.对于add的时机，由于处理到A[i+1]及其后面的数据时，才会使用到A[i]对于B的影响，因此，需要在计算完A[i]后再在B上加上A[i]的影响。