【机器学习基础】TP,TN,FP,FN,Precision，Recall，PR曲线，AP，MAP，TPR，FPR,ROC曲线，AUC值等的解释

1.TP,TN,FP,FN：

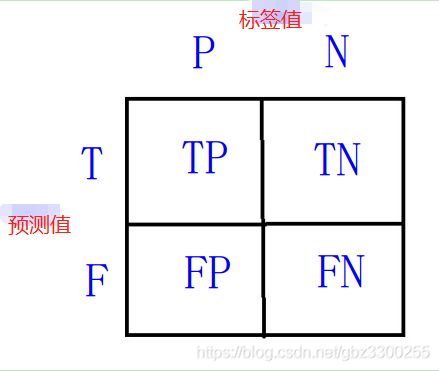
    下面两个图说的就很明白了吧。左侧有点混淆矩阵的感觉

    P：标签为正样本。

    N：标签为负样本。

    T：预测对了。

    F：预测错了

    TP：正样本被预测为正样本。

    FN：正样本被预测为负样本。 预测错了呗

    FP：负样本被预测为正样本。 预测错了呗

    TN：负样本被预测为负样本。  

  

 

2.PR曲线计算：

2.1 PR曲线画图要知道P是啥  R是啥。

        正样本精确率为：Precision=TP/(TP+FP)，表示的是  正样本识别正确总数 / 识别为正样本的样本总数

        正样本召回率为：Recall=TP/(TP+FN)，表示的是 正样本识别正确总数 / 正样本的样本总数

        上面这个Precision Recall就是PR曲线的P和R了，下面这个图太形象了。

                                                            

2.2.画PR曲线方法：

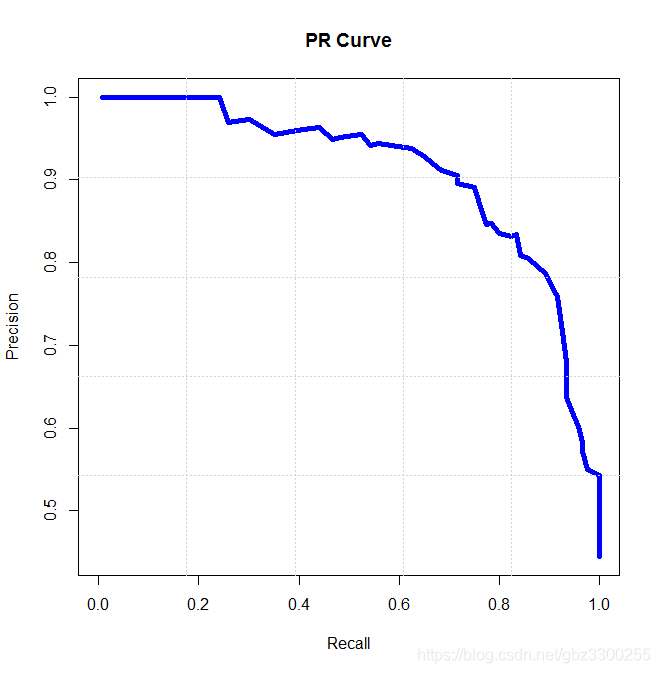
        通过置信度就可以对所有样本进行排序，再逐个样本的选择阈值，在该样本之前的都属于正例，该样本之后的都属于负例。每一个样本作为划分阈值时，都可以计算对应的precision和recall，那么就可以以此绘制曲线。下面就是类似的曲线。注意这个置信度排序是由高到低进行的。所以先按高阈值画图的话，precision会高，而recall就会低些。反之到了低阈值区域，precision会变低，因为负样本被识别成正样本的几率大大增加，而reacll就会变高，因为正样本几乎不会呗漏下了啊。

                                          

横轴就是recall，纵轴就是precision，曲线越接近右上角，说明其性能越好，可以用该曲线与坐标轴包围的面积来定量评估，值在0～1之间。

3.AP,MAP计算

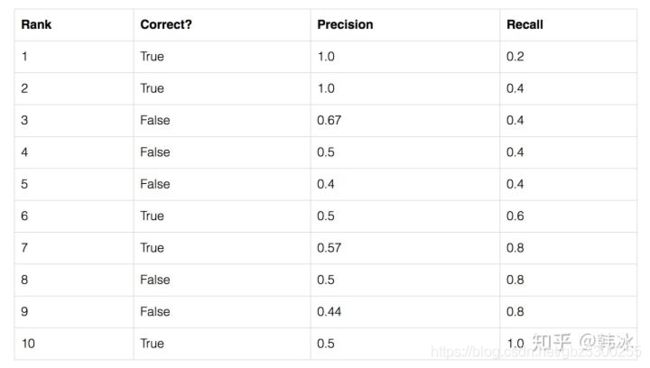
        假设我们的数据集中共有5个待检测的物体，我们的模型给出了10个候选框，我们按照模型给出的置信度由高到低对候选框进行排序。

                           .

        表格第二列表示该候选框是否预测正确（即是否存在某个待检测的物体与该候选框的iou值大于0.5，相当于标签值）第三列和第四列表示以该行所在候选框置信度为阈值时，Precision和Recall的值。我们以表格的第三行为例进行计算：

按第三行阈值，前三个都被预测为true。

TP = 2        编号1 2为true且被识别为true了

FP = 1        编号 3 为false且被识别为true了

FN = 3        编号6 7 10 为true且被识别为false了

根据公式：Precision = TP/(TP+FP) = 2 / 2 + 1 = 0.67

                    Recall=TP/(TP+FN) = 2 / 5 = 0.4

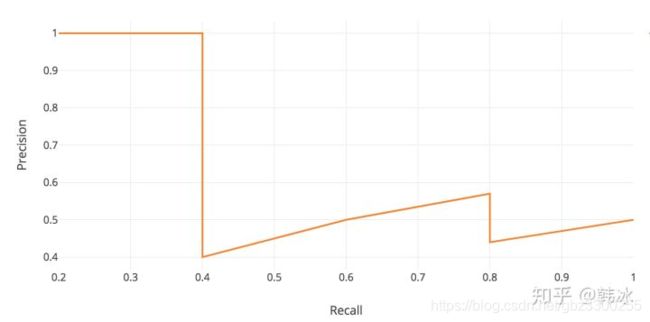
画出PR曲线图如下：

在PR曲线上进行的计算。AP 全称Average Precision。

                  

随便找的一个，下次补全一下。 https://zhuanlan.zhihu.com/p/88896868 这个里面介绍AP计算写的很清晰就是绿线线面的面积。

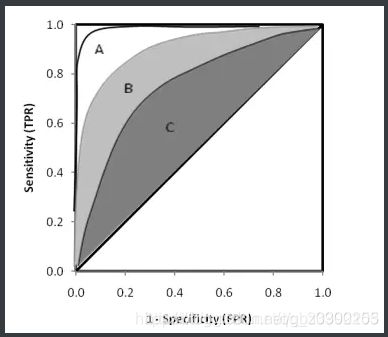
4.ROC曲线计算

4.1 计算它有涉及到两个公式

TPR=TP / (FN + TP​ )               正样本识别正确总数 / 正例总数

FPR=FP / (TN + FP​ ​)              负样本识别错误总数 / 负例总数

4.2 ROC曲线的绘制步骤如下：

        a.假设已经得出一系列样本被划分为正类的概率Score值，按照由大到小排序。

        b.从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。举例来说，对于某个样本，其“Score”值为0.6，那么“Score”值大于等于0.6的样本都被认为是正样本，而其他样本则都认为是负样本。

        c.每次选取一个不同的threshold，得到一组FPR和TPR，以FPR值为横坐标和TPR值为纵坐标，即ROC曲线上的一点。

        d.根据3中的每个坐标点，画图。

                                                               

    e.其中有4个关键的点：仔细看第2条就不难理解下面这几个点了。

    点(0,0)：FPR=TPR=0，分类器预测所有的样本都为负样本。

    点(1,1)：FPR=TPR=1，分类器预测所有的样本都为正样本。

    点(0,1)：FPR=0, TPR=1，此时FN＝0且FP＝0，所有的正样本都正确分类。

    点(1,0)：FPR=1，TPR=0，此时TP＝0且TN＝0，最差分类器，所有正样本都没识对。

    ROC曲线图中的点对应的模型，它们的不同之处仅仅是在分类时选用的阈值(Threshold)不同，每个点所选用的阈值都对应某个样本被预测为正类的概率值。

    ROC曲线相对于PR曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变，即对正负样本不均衡问题不敏感。

4.3 AUC计算：

        AUC表示ROC曲线下的面积，主要用于衡量模型的泛化性能，即分类效果的好坏。AUC是衡量二分类模型优劣的一种评价指标，表示正例排在负例前面的概率。一般在分类模型中，预测结果都是以概率的形式表现，如果要计算准确率，通常都会手动设置一个阈值来将对应的概率转化成类别，这个阈值也就很大程度上影响了模型准确率的计算。之所以采用AUC来评价，主要还是考虑到ROC曲线本身并不能直观的说明一个分类器性能的好坏，而AUC值作为一个数量值，具有可比较性，可以进行定量的比较。

4.4 AUC值对模型性能的判断标准：

1. AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
2. 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
3. AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
4. AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测

参考文献1：https://blog.csdn.net/qq_41994006/article/details/81051150 

参考文献2：https://blog.csdn.net/b876144622/article/details/80009867

参考文献3：https://www.zhihu.com/question/53405779

参考文献4：https://www.cnblogs.com/Tom-Ren/p/11054605.html

参考文献5：https://blog.csdn.net/qq_30992103/article/details/99730059 专门讲ROC曲线的 很经典

参考文献6：https://mp.weixin.qq.com/s?__biz=MzA3NDIyMjM1NA==&mid=2649031923&idx=1&sn=bcc3cef468f44d0a6de5b87ea00e5e5b&chksm=8712ba8eb065339829ee84e7398e23d85dd7c4c7c154b96caead73c8815f887bb3c1bb7de063&token=598159941&lang=zh_CN#rd  这个是经典