2020年数二真题(重点题讲解)
选择题

解析: 看到题目要求的是 f ( n ) ( x ) f^{(n)}(x) f(n)(x),而且 n ≥ 3 n\geq3 n≥3,我们首先想到泰勒展开式。 而且题目都说了,求的是x=0处的值,很明显的让你想到麦克劳林公式。我们先看下常用麦克劳林公式如下:

对于 l n ( 1 − x ) = − x − x 2 2 − x 3 3 − . . . − x n n ; ln(1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-...-\frac{x^n}{n}; ln(1−x)=−x−2x2−3x3−...−nxn;
所以 f ( x ) = x 2 l n ( 1 − x ) = − x 3 − x 4 2 − x 5 3 − . . . − x n n − 2 − x n + 2 n f(x)=x^2ln(1-x)=-x^3-\frac{x^4}{2}-\frac{x^5}{3}-...-\frac{x^n}{n-2}-\frac{x^{n+2}}{n} f(x)=x2ln(1−x)=−x3−2x4−3x5−...−n−2xn−nxn+2;
而泰勒公式如下;我们从泰勒公式里面可以看到只需要找到 x n x^n xn的系数值,就能知道 f ( n ) ( 0 ) f^{(n)}(0) f(n)(0)的值
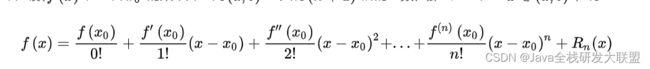
而 f ( x ) = x 2 l n ( 1 − x ) = − x 3 − x 4 2 − x 5 3 − . . . − x n n − 2 − x n + 2 n f(x)=x^2ln(1-x)=-x^3-\frac{x^4}{2}-\frac{x^5}{3}-...-\frac{x^n}{n-2}-\frac{x^{n+2}}{n} f(x)=x2ln(1−x)=−x3−2x4−3x5−...−n−2xn−nxn+2;中 x n x^n xn的系数是 1 n − 2 \frac{1}{n-2} n−21;
所以啊我们就可以得到一个等式即 f ( n ) ( 0 ) n ! = − 1 n − 2 \frac{f^{(n)(0)}}{n!}=-\frac{1}{n-2} n!f(n)(0)=−n−21 ,所以 f ( n ) ( 0 ) = − n ! n − 2 f^{(n)}(0)=-\frac{n!}{n-2} f(n)(0)=−n−2n!。 本题选A

正确答案: B
解析: 本题给的 f ( x , y ) f(x,y) f(x,y)是一个分段函数,它不是一个连续函数。所以这个时候要在间断点求导数值,只能用导数的定义式,而不能用其他方法。
先来讨论① , ∂ f ∂ x ∣ ( 0 , 0 ) = lim x → 0 f ( x , 0 ) − f ( 0 , 0 ) x − 0 = x − 0 x = 1 \frac{\partial f}{\partial x}|_{(0,0)}=\lim_{x\to0}\frac{f(x,0)-f(0,0)}{x-0}=\frac{x-0}{x}=1 ∂x∂f∣(0,0)=limx→0x−0f(x,0)−f(0,0)=xx−0=1,所以①是对的。
再看②, ∂ 2 f ∂ x ∂ y ∣ ( 0 , 0 ) = ∂ f ∂ x ∣ ( 0 , y ) − ∂ f ∂ x ∣ ( 0 , 0 ) y − 0 = ∂ f ∂ x ∣ ( 0 , y ) − 1 y − 0 \frac{\partial ^2 f}{\partial x \partial y}|_{(0,0)}=\frac{\frac{\partial f}{\partial x}|_{(0,y)}-\frac{\partial f}{\partial x}|_{(0,0)}}{y-0}=\frac{\frac{\partial f}{\partial x}|_{(0,y)}-1}{y-0} ∂x∂y∂2f∣(0,0)=y−0∂x∂f∣(0,y)−∂x∂f∣(0,0)=y−0∂x∂f∣(0,y)−1
而 ∂ f ∂ x ∣ ( 0 , y ) = lim x → 0 f ( x , y ) − f ( 0 , y ) x − 0 = lim x → 0 x y − y x = lim x → 0 x − 1 x . y \frac{\partial f}{\partial x}|_{(0,y)}=\lim_{x\to0}\frac{f(x,y)-f(0,y)}{x-0}=\lim_{x\to0}\frac{xy-y}{x}=\lim_{x\to0}\frac{x-1}{x}.y ∂x∂f∣(0,y)=limx→0x−0f(x,y)−f(0,y)=limx→0xxy−y=limx→0xx−1.y 不存在,所以②是错的
再看③,当 ( x , y ) → ( 0 , 0 ) (x,y)\to(0,0) (x,y)→(0,0)时,那 x x x和 y y y肯定都不等于0,那 f ( x , y ) = x y f(x,y)=xy f(x,y)=xy,所以 lim ( x , y ) → ( 0 , 0 ) f ( x , y ) = 0 \lim_{(x,y)\to(0,0)}f(x,y)=0 lim(x,y)→(0,0)f(x,y)=0,所以③是对的
再看④,其实③和④一样,所以④是对的

正确答案:
解题思路: 看到题目里面有 f ′ ( x ) f^\prime(x) f′(x)和 f ( x ) f(x) f(x)比较大小的,于是首先要想到构造 F ( x ) = f ( x ) e x F(x)=\frac{f(x)}{e^x} F(x)=exf(x),因为 F ′ ( x ) F^\prime(x) F′(x)里面会出现 f ′ ( x ) f^\prime(x) f′(x)和 f ( x ) f(x) f(x)作差的情况



正确答案:C
解题思路:
我们先回顾下伴随矩阵的一些性质

题目中说了A不可逆,所以r(A)<4, 且|A|=0, 又因为 a 12 a_{12} a12的代数余子式 A 12 ≠ 0 A_{12}\neq0 A12=0,所以 r ( A ∗ ) ≥ 1 r(A^*)\geq1 r(A∗)≥1 ,且可以知道 α 1 , α 3 , α 4 \alpha_1,\alpha_3,\alpha_4 α1,α3,α4线性无关。 根据上面的性质(3),而当 r ( A ∗ ) = 1 r(A^*)=1 r(A∗)=1的时候,r(A)=n-1=3,
而 A A ∗ = A ∗ A = ∣ A ∣ E = AA^*=A^*A=|A|E= AA∗=A∗A=∣A∣E=,在本题里面 A ∗ A = 0 A^*A=0 A∗A=0,所以A的列向量都是 A ∗ X = 0 A^*X=0 A∗X=0的解。 但 r ( A ∗ ) = 1 r(A^*)=1 r(A∗)=1,所以基础解系的个数是n-1=3. 而A的列向量中 α 1 , α 3 , α 4 \alpha_1,\alpha_3,\alpha_4 α1,α3,α4线性无关,所以刚好构成基础解系,所以本题选C
填空题
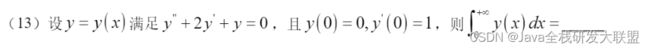
解题思路:
先写出特征方程 λ 2 + 2 λ + 1 = 0 \lambda^2+2\lambda+1=0 λ2+2λ+1=0,然后很容易就知道特征根 λ 1 = λ 2 = − 1 , \lambda_1=\lambda_2=-1, λ1=λ2=−1,所以通解 y = ( C 1 + C 2 x ) e − x y=(C_1+C_2x)e^{-x} y=(C1+C2x)e−x,然后根据题目给的条件 y ( 0 ) = 0 , y ′ ( 0 ) = 1 y(0)=0,y^\prime(0)=1 y(0)=0,y′(0)=1,可以算出 C 1 = 0 , C 2 = 1 C_1=0,C_2=1 C1=0,C2=1, 所以啊 y = x e − x y=xe^{-x} y=xe−x, 题目让我们求 ∫ 0 + ∞ x e − x d x \int_0^{+\infty}xe^{-x}dx ∫0+∞xe−xdx,这就考察你伽马函数的公式了, ∫ 0 + ∞ x e − x d x = Γ ( 1 ) = 1 \int_0^{+\infty}xe^{-x}dx=Γ(1)=1 ∫0+∞xe−xdx=Γ(1)=1
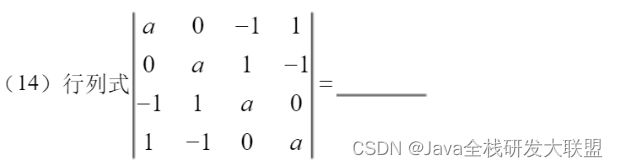
正确答案: a 4 − 4 a 2 a^4-4a^2 a4−4a2
解题思路:
∣ a 0 − 1 1 0 a 1 − 1 − 1 1 a 0 1 − 1 0 a ∣ = > 第 2 行 加 到 第 1 行 上 \left| \begin{matrix} a& 0&-1&1\\ 0&a&1&-1 \\ -1&1&a&0\\ 1&-1&0&a \end{matrix} \right|=>^{第2行加到第1行上} ∣∣∣∣∣∣∣∣a0−110a1−1−11a01−10a∣∣∣∣∣∣∣∣=>第2行加到第1行上
∣ a a 0 0 0 a 1 − 1 − 1 1 a 0 1 − 1 0 a ∣ = > 利 用 r 3 和 r 4 把 行 列 式 右 上 角 打 成 0 \left| \begin{matrix} a& a&0&0\\ 0&a&1&-1 \\ -1&1&a&0\\ 1&-1&0&a \end{matrix} \right|=>^{利用r_3和r_4把行列式右上角打成0} ∣∣∣∣∣∣∣∣a0−11aa1−101a00−10a∣∣∣∣∣∣∣∣=>利用r3和r4把行列式右上角打成0
∣ a a 0 0 2 a a − 2 a 0 0 − 1 1 a 0 1 − 1 0 a ∣ \left| \begin{matrix} a& a&0&0\\ \frac{2}{a}&a-\frac{2}{a}&0&0 \\ -1&1&a&0\\ 1&-1&0&a \end{matrix} \right| ∣∣∣∣∣∣∣∣aa2−11aa−a21−100a0000a∣∣∣∣∣∣∣∣= [ a ( a − 2 a ) − 2 ] ∗ a 2 = a 4 − 4 a 2 [a(a-\frac{2}{a})-2]*a^2=a^4-4a^2 [a(a−a2)−2]∗a2=a4−4a2
解答题

解题思路:
先求斜率k, k = lim x → + ∞ y x = x x ( 1 + x ) x = ( x 1 + x ) x = e x l n ( 1 − 1 1 + x ) = e − x 1 + x = e − 1 k=\lim_{x\to+\infty}\frac{y}{x}=\frac{x^x}{(1+x)^x}=(\frac{x}{1+x})^x=e^{xln(1-\frac{1}{1+x})}=e^{-\frac{x}{1+x}}=e^{-1} k=limx→+∞xy=(1+x)xxx=(1+xx)x=exln(1−1+x1)=e−1+xx=e−1
然后再求截距b, b = lim x → + ∞ y − k x = x 1 + x ( 1 + x ) x − x e = x ( x x ( 1 + x ) x − 1 e ) = x [ e x l n ( 1 − 1 1 + x ) − e − 1 ] = b=\lim_{x\to+\infty} y-kx=\frac{x^{1+x}}{(1+x)^x}-\frac{x}{e}=x(\frac{x^x}{(1+x)^x}-\frac{1}{e})=x[e^{xln(1-\frac{1}{1+x})}-e^{-1}]= b=limx→+∞y−kx=(1+x)xx1+x−ex=x((1+x)xxx−e1)=x[exln(1−1+x1)−e−1]=
e − 1 x [ e x l n ( 1 − 1 1 + x ) + 1 − 1 ] = = = > ( 令 x = 1 t ) = e − 1 . e − 1 t l n ( 1 + t ) + 1 − 1 t = e − 1 . − 1 t l n ( 1 + t ) + 1 t = e − 1 . − t − l n ( 1 + t ) t 2 = 1 2 e e^{-1}x[e^{xln(1-\frac{1}{1+x})+1}-1]===>^{(令x=\frac{1}{t})}=e^{-1}.\frac{e^{-\frac{1}{t}ln(1+t)+1}-1}{t}=e^{-1}. \frac{-\frac{1}{t}ln(1+t)+1}{t}=e^{-1}.-\frac{t-ln(1+t)}{t^2}=\frac{1}{2e} e−1x[exln(1−1+x1)+1−1]===>(令x=t1)=e−1.te−t1ln(1+t)+1−1=e−1.t−t1ln(1+t)+1=e−1.−t2t−ln(1+t)=2e1
所以斜渐近线方程是 y = e − 1 x + 1 2 e y=e^{-1}x+\frac{1}{2e} y=e−1x+2e1
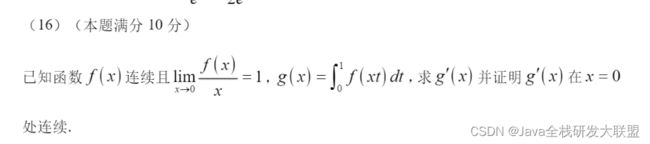
解题思路: 题目让我们证明 g ′ ( x ) g^\prime(x) g′(x)在x=0处连续,那我们肯定要把 g ′ ( x ) g^\prime(x) g′(x)表达式求出来,要求 g ′ ( x ) g^\prime(x) g′(x)必须要先求 g ( x ) g(x) g(x)表达式。
从题目条件 lim x → 0 f ( x ) x = 1 \lim_{x\to0}\frac{f(x)}{x}=1 limx→0xf(x)=1,就可以知道 f ( 0 ) = 0 , f ′ ( 0 ) = 1 f(0)=0, f^\prime(0)=1 f(0)=0,f′(0)=1。
而题目又说了 g ( x ) = ∫ 0 1 f ( x t ) d t g(x)=\int_0^1f(xt)dt g(x)=∫01f(xt)dt,而 ∫ 0 1 f ( x t ) d t = 1 x ∫ 0 1 f ( x t ) d ( x t ) = 1 x ∫ 0 x f ( u ) d u \int_0^1f(xt)dt=\frac{1}{x}\int_0^1f(xt)d(xt)=\frac{1}{x}\int_0^xf(u)du ∫01f(xt)dt=x1∫01f(xt)d(xt)=x1∫0xf(u)du
所以 g ( x ) = { 0 , x = 0 1 x ∫ 0 x f ( u ) d u , x ≠ 0 (1) g(x)=\begin{cases} 0,\quad x= 0 \\[2ex] \frac{1}{x}\int_0^xf(u)du, \quad x\neq0 \end{cases} \tag{1} g(x)=⎩⎨⎧0,x=0x1∫0xf(u)du,x=0(1)
所以啊 g ( x ) g(x) g(x)是一个分段函数,我们要计算 g ′ ( 0 ) g^\prime(0) g′(0)需要用导数定义式。
g ′ ( 0 ) = lim x → 0 1 x ∫ 0 x f ( u ) d u − 0 x − 0 = ∫ 0 x f ( u ) d u x 2 = f ( x ) 2 x = 1 2 g^\prime(0)=\lim_{x\to0}\frac{\frac{1}{x}\int_0^xf(u)du-0}{x-0}=\frac{\int_0^xf(u)du}{x^2}=\frac{f(x)}{2x}=\frac{1}{2} g′(0)=limx→0x−0x1∫0xf(u)du−0=x2∫0xf(u)du=2xf(x)=21
当 x ≠ 0 x\neq0 x=0时, g ′ ( x ) = − 1 x 2 ∫ 0 x f ( u ) d u + 1 x f ( x ) g^\prime(x)=-\frac{1}{x^2}\int_0^xf(u)du+\frac{1}{x}f(x) g′(x)=−x21∫0xf(u)du+x1f(x)
所以啊
g ′ ( x ) = { 1 2 , x = 0 − 1 x 2 ∫ 0 x f ( u ) d u + 1 x f ( x ) , x ≠ 0 (1) g^\prime(x)=\begin{cases} \frac{1}{2},\quad x= 0 \\[2ex] -\frac{1}{x^2}\int_0^xf(u)du+\frac{1}{x}f(x), \quad x\neq0 \end{cases} \tag{1} g′(x)=⎩⎨⎧21,x=0−x21∫0xf(u)du+x1f(x),x=0(1)
那我们再计算下 lim x → 0 g ′ ( x ) = x f ( x ) − ∫ 0 x f ( u ) d u x 2 = f ( x ) + x f ′ ( x ) − f ( x ) 2 x = f ′ ( x ) 2 = 1 2 \lim_{x\to0}g^\prime(x)=\frac{xf(x)-\int_0^xf(u)du}{x^2}=\frac{f(x)+xf^\prime(x)-f(x)}{2x}=\frac{f^\prime(x)}{2}=\frac{1}{2} limx→0g′(x)=x2xf(x)−∫0xf(u)du=2xf(x)+xf′(x)−f(x)=2f′(x)=21
所以 g ′ ( x ) g^\prime(x) g′(x)在x=0处连续。

解题思路:要算极值,就要找驻点,就必须要算x,y的偏导数
f x ( x , y ) = 3 x 2 − y ; f_x(x,y)=3x^2-y; fx(x,y)=3x2−y; f y ( x , y ) = 24 y 2 − x f_y(x,y)=24y^2-x fy(x,y)=24y2−x
{ f x ( x , y ) = 3 x 2 − y = 0 ; f y ( x , y ) = 24 y 2 − x = 0 = > 得 { x = 0 ; y = 0 或 { x = 1 6 ; y = 1 12 \begin{cases} f_x(x,y)=3x^2-y=0;\\ f_y(x,y)=24y^2-x=0 \end{cases}=>得\begin{cases} x=0;\\ y=0 \end{cases} 或\begin{cases} x=\frac{1}{6};\\ y=\frac{1}{12} \end{cases} {fx(x,y)=3x2−y=0;fy(x,y)=24y2−x=0=>得{x=0;y=0或{x=61;y=121
而 A = f x x = 6 x , B = f x y = − 1 , C = f y y = 48 y , A=f_{xx}=6x, B=f_{xy}=-1,C= f_{yy}=48y, A=fxx=6x,B=fxy=−1,C=fyy=48y,
当驻点为(0,0)时, A = 0 , B = − 1 , C = 0 A=0,B=-1,C=0 A=0,B=−1,C=0,则 A C − B 2 < 0 AC-B^2<0 AC−B2<0,所以(0,0)不是极值点
当驻点是 ( 1 6 , 1 12 ) (\frac{1}{6},\frac{1}{12}) (61,121)时, A = 1 , B = − 1 , C = 4 A=1,B=-1,C=4 A=1,B=−1,C=4.则 A C − B 2 > 0 AC-B^2>0 AC−B2>0,且A>0,所以是极小值。 f ( 1 6 , 1 12 ) = − 1 216 f(\frac{1}{6},\frac{1}{12})=-\frac{1}{216} f(61,121)=−2161;

解题思路: 我们先要把 f ( x ) f(x) f(x)表达式求出来
题目给了我们一个等式
2 f ( x ) + x 2 f ( 1 x ) = x 2 + 2 x 1 + x 2 ① 2f(x)+x^2f(\frac{1}{x})=\frac{x^2+2x}{\sqrt{1+x^2}} ① 2f(x)+x2f(x1)=1+x2x2+2x①
我们把x的位置换成 1 x \frac{1}{x} x1,等式就变成 2 f ( 1 x ) + 1 x 2 f ( x ) = 1 x 2 + 2 x 1 + 1 x 2 = 1 + 2 x x 1 + x 2 ② 2f(\frac{1}{x})+\frac{1}{x^2}f(x)=\frac{\frac{1}{x^2}+\frac{2}{x}}{\sqrt{1+\frac{1}{x^2}}}=\frac{1+2x}{x\sqrt{1+x^2}} ② 2f(x1)+x21f(x)=1+x21x21+x2=x1+x21+2x②
我们联立①和②就能算出 f ( x ) = x 1 + x 2 f(x)=\frac{x}{\sqrt{1+x^2}} f(x)=1+x2x
然后题目让我们求的是旋转体的体积
即 ∫ 1 2 3 2 2 π y x d y \int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}2πyxdy ∫21232πyxdy (注:旋转体中每一个微元的周长是2πy,然后宽是x,厚度是dy)
我们已经知道了 y = x 1 + x 2 y=\frac{x}{\sqrt{1+x^2}} y=1+x2x,那我们如何反过来用y来表示x呢?
我们可以这样干 y = x 1 + x 2 y=\frac{x}{\sqrt{1+x^2}} y=1+x2x两边平方, y 2 = x 2 1 + x 2 y^2=\frac{x^2}{1+x^2} y2=1+x2x2,即 ( 1 − y 2 ) x 2 = y 2 (1-y^2)x^2=y^2 (1−y2)x2=y2,即 x = y 1 − y 2 x=\frac{y}{\sqrt{1-y^2}} x=1−y2y
所以 ∫ 1 2 3 2 2 π y x d y = ∫ 1 2 3 2 2 π y y 1 − y 2 d y \int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}2πyxdy=\int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}2πy\frac{y}{\sqrt{1-y^2}}dy ∫21232πyxdy=∫21232πy1−y2ydy
对于这个积分,我们可以想到三角换元法令 y = s i n t , t ∈ [ π 6 , π 3 ] y=sint,t\in[\frac{π}{6},\frac{π}{3}] y=sint,t∈[6π,3π],则原积分写成
∫ π 6 π 3 2 π s i n 2 t d t = π 2 6 \int_{\frac{π}{6}}^{\frac{π}{3}}2πsin^2tdt=\frac{π^2}{6} ∫6π3π2πsin2tdt=6π2

解题思路:这道题太简单了,一看到积分函数里面有 x 2 + y 2 x^2+y^2 x2+y2,首先想到利用极坐标来解决
所以原积分就可以转换成 ∫ 0 π 4 d θ ∫ 1 c o s θ 2 c o s θ r r c o s θ . r d r = 3 2 ∫ 0 π 4 s e c 3 θ d θ \int_0^\frac{π}{4}d\theta\int_\frac{1}{cos\theta}^\frac{2}{cos\theta} \frac{r}{rcos\theta}.rdr=\frac{3}{2}\int_0^\frac{π}{4}sec^3\theta d \theta ∫04πdθ∫cosθ1cosθ2rcosθr.rdr=23∫04πsec3θdθ
∫ s e c 3 θ d θ = ∫ s e c θ d ( t a n θ ) = s e c θ t a n θ − ∫ t a n 2 θ s e c θ d θ = s e c θ t a n θ − ∫ ( s e c 2 θ − 1 ) s e c θ d θ = s e c θ t a n θ − ∫ s e c 3 θ + ∫ s e c θ d θ = s e c θ t a n θ − ∫ s e c 3 θ + l n ∣ s e c θ + t a n θ ∣ \int sec^3 \theta d\theta=\int sec\theta d(tan\theta)=sec\theta tan\theta-\int tan^2\theta sec\theta d\theta=sec\theta tan\theta-\int(sec^2\theta-1)sec\theta d\theta=sec\theta tan\theta-\int sec^3\theta+\int sec\theta d\theta=sec\theta tan\theta-\int sec^3\theta+ln|sec\theta+tan \theta| ∫sec3θdθ=∫secθd(tanθ)=secθtanθ−∫tan2θsecθdθ=secθtanθ−∫(sec2θ−1)secθdθ=secθtanθ−∫sec3θ+∫secθdθ=secθtanθ−∫sec3θ+ln∣secθ+tanθ∣
所以 ∫ s e c 3 θ d θ = s e c θ t a n θ + l n ∣ s e c θ + t a n θ ∣ 2 \int sec^3 \theta d\theta=\frac{sec\theta tan\theta+ln|sec \theta+tan \theta|}{2} ∫sec3θdθ=2secθtanθ+ln∣secθ+tanθ∣
所以 3 2 ∫ 0 π 4 s e c 3 θ d θ \frac{3}{2}\int_0^\frac{π}{4}sec^3\theta d \theta 23∫04πsec3θdθ很容易算出来是 3 2 4 + 3 l n ( 1 + 2 ) 4 \frac{3\sqrt{2}}{4}+\frac{3ln(1+\sqrt2)}{4} 432+43ln(1+2)

(1)证明: 令 F ( x ) = ∫ 1 x e t 2 d t − ( 2 − x ) e x 2 F(x)=\int_1^xe^{t^2}dt-(2-x)e^{x^2} F(x)=∫1xet2dt−(2−x)ex2
而 F ( 1 ) = − e F(1)=-e F(1)=−e, F ( 2 ) = ∫ 1 2 e t 2 d t F(2)=\int_1^2e^{t^2}dt F(2)=∫12et2dt, F ( 1 ) < 0 , F ( 2 ) > 0 F(1)<0,F(2)>0 F(1)<0,F(2)>0.由介值定理可得必定有 ξ ∈ ( 1 , 2 ) , f ( ξ ) = ( 2 − ξ ) e ξ 2 \xi\in(1,2),f(\xi)=(2-\xi)e^{\xi^2} ξ∈(1,2),f(ξ)=(2−ξ)eξ2
(2)证明: 题目让我们证明 f ( 2 ) = l n 2. η e η 2 f(2)=ln2.\eta e^{\eta^2} f(2)=ln2.ηeη2,我们发现
f ( 2 ) = ∫ 1 x e t 2 d t f(2)=\int_1^xe^{t^2}dt f(2)=∫1xet2dt 这个值根本不好算。而且一想到本题应该不是考察你的计算能力,而是考察你的逻辑推导能力,所以另想它法、多半是考察几个定理,比如罗尔定理,拉格朗日中值定理,介值定理,积分中值定理,柯西中值定理等等。
然后我们再观察下 f ( 2 ) = l n 2. η e η 2 f(2)=ln2.\eta e^{\eta^2} f(2)=ln2.ηeη2这个式子,有 e η 2 e^{\eta^2} eη2,而 f ( x ) f(x) f(x)的导数 f ′ ( x ) = e x 2 f^\prime(x)=e^{x^2} f′(x)=ex2。
所以啊题目让我们证明的 f ( 2 ) = l n 2. η e η 2 f(2)=ln2.\eta e^{\eta^2} f(2)=ln2.ηeη2,里面出现了类似于 f ( x ) f(x) f(x)和 f ′ ( x ) f^\prime(x) f′(x)这样的式子,而且我们再观察到 f ( 2 ) = l n 2. η e η 2 f(2)=ln2.\eta e^{\eta^2} f(2)=ln2.ηeη2里面有 f ( 2 ) f(2) f(2)和 l n 2 ln2 ln2,都有2,那我们构造一个函数 g ( x ) = l n x g(x)=lnx g(x)=lnx出来,在上面说的那些定理中,出现两个函数 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)的也就只有柯西中值定理了。我们就用这个定理来解题。
存在 η ∈ ( 1 , 2 ) \eta \in(1,2) η∈(1,2)使得 f ( 2 ) − f ( 1 ) g ( 2 ) − g ( 1 ) = f ′ ( η ) g ′ ( η ) \frac{f(2)-f(1)}{g(2)-g(1)}=\frac{f^\prime(\eta)}{g^\prime(\eta)} g(2)−g(1)f(2)−f(1)=g′(η)f′(η),即 f ( 2 ) l n 2 = e η 2 1 η \frac{f(2)}{ln2}=\frac{e^{\eta^2}}{\frac{1}{\eta}} ln2f(2)=η1eη2, 即 f ( 2 ) = l n 2. η e η 2 f(2)=ln2.\eta e^{\eta^2} f(2)=ln2.ηeη2证明完毕

解题思路: 假设M点的坐标是 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),则切线方程是 y − − y 0 = ( x − x 0 ) f ′ ( x 0 ) y--y_0=(x-x_0)f^\prime(x_0) y−−y0=(x−x0)f′(x0), 然后T点的坐标也可以根据这个切线方程算出来是 ( x 0 f ′ ( x 0 ) − y 0 f ′ ( x 0 ) , 0 ) (\frac{x_0f^\prime(x_0)-y_0}{f^\prime(x_0)},0) (f′(x0)x0f′(x0)−y0,0),然后就可以算出 S △ M T P = 1 2 [ x 0 − ( x 0 f ′ ( x 0 ) − y 0 f ′ ( x 0 ) ) ] . y 0 = 1 2 y 0 2 f ′ ( x 0 ) S_△MTP=\frac{1}{2}[x_0-(\frac{x_0f^\prime(x_0)-y_0}{f^\prime(x_0)})].y_0=\frac{1}{2}\frac{y_0^2}{f^\prime(x_0)} S△MTP=21[x0−(f′(x0)x0f′(x0)−y0)].y0=21f′(x0)y02
而曲线 y = f ( x ) y=f(x) y=f(x),直线MP,以及x轴围成的图形面积是 ∫ 0 x f ( x ) d x \int_0^xf(x)dx ∫0xf(x)dx
所以根据题目说的面积之比是3:2,则有
y 2 2 y ′ ∫ 0 x y d x = 2 3 \frac{\frac{y^2}{2y^\prime}}{\int_{0}^{x}ydx}=\frac{2}{3} ∫0xydx2y′y2=32
即 ∫ 0 x y d x = 3 y 2 4 y ′ ] \int_0^xydx=\frac{3y^2}{4y^\prime}] ∫0xydx=4y′3y2]。 两边求导得 y = 3 4 . 2 y y ′ y ′ − y 2 y ′ ′ ( y ′ ) 2 y=\frac{3}{4}.\frac{2yy^\prime y^\prime-y^2y^{\prime\prime}}{(y^\prime)^2} y=43.(y′)22yy′y′−y2y′′,整理得 3 y y ′ ′ = 2 ( y ′ ) 2 3yy^{\prime\prime}=2(y^\prime)^2 3yy′′=2(y′)2, 令 y ′ = p y^\prime=p y′=p,则 y ′ ′ = p d p d y y^{\prime\prime}=p\frac{dp}{dy} y′′=pdydp,代入式子中得 3 y p d p d y = 2 p 2 3yp\frac{dp}{dy}=2p^2 3ypdydp=2p2,解得 p = C 1 y 2 3 p=C_1y^{\frac{2}{3}} p=C1y32,即 d y d x = C 1 y 2 3 \frac{dy}{dx}=C_1y^{\frac{2}{3}} dxdy=C1y32,解得 3 y 1 3 = C 1 x + C 2 3y^{\frac{1}{3}}=C_1x+C_2 3y31=C1x+C2,
题目中说了经过原点,所以把(0,0)代入算出 C 2 = 0 C_2=0 C2=0,所以 y = C x 3 y=Cx^3 y=Cx3, 又因为题目说了 f ( x ) f(x) f(x)单增,所以 C > 0 C>0 C>0
本题答案就是 y = C x 3 y=Cx^3 y=Cx3, ( C > 0 ) (C>0) (C>0)

解题思路:
(1)看到题目里面的 X = P Y X=PY X=PY,首先想到矩阵合同的性质,①矩阵合同,则正负惯性指数相同 ②矩阵合同则秩相同
我们先看 g ( y 1 , y 2 , u 3 ) g(y_1,y_2,u_3) g(y1,y2,u3)的矩阵=
{ 1 1 0 1 1 0 0 0 4 } (4) \left\{ \begin{matrix} 1 & 1 & 0\\ 1 & 1 & 0 \\ 0 & 0 & 4 \end{matrix} \right\} \tag{4} ⎩⎨⎧110110004⎭⎬⎫(4)
很显然秩是2. 所以 f ( x 1 , x 2 , x 3 ) f(x_1,x_2,x_3) f(x1,x2,x3)矩阵的秩也应该是2,那行列式就是0,即
∣ 1 a a a 1 a a a 1 ∣ = 0 (3) \left| \begin{matrix} 1 & a & a\\ a & 1 & a \\ a & a & 1 \end{matrix} \right| \tag{3}=0 ∣∣∣∣∣∣1aaa1aaa1∣∣∣∣∣∣=0(3)
算出 a = 1 a=1 a=1(舍去)或 a = − 1 2 a=-\frac{1}{2} a=−21, (注:如果a=1,则矩阵的秩就是1了,不符合条件), 所以 a = − 1 2 a=-\frac{1}{2} a=−21
(2)由第1问结论,可以得到 f ( x 1 , x 2 , x 3 ) = x 1 2 + x 2 2 + x 3 2 − x 1 x 2 − x 1 x 3 − x 2 x 3 = ( x 1 − 1 2 x 2 − 1 2 x 3 ) 2 + 3 4 x 2 2 + 3 4 x 3 2 − 3 2 x 2 x 3 = ( x 1 − 1 2 x 2 − 1 2 x 3 ) 2 + 3 4 ( x 2 − x 3 ) 2 f(x_1,x_2,x_3)=x_1^2+x_2^2+x_3^2-x_1x_2-x_1x_3-x_2x_3=(x_1-\frac{1}{2}x_2-\frac{1}{2}x_3)^2+\frac{3}{4}x_2^2+\frac{3}{4}x_3^2-\frac{3}{2}x_2x_3=(x_1-\frac{1}{2}x_2-\frac{1}{2}x_3)^2+\frac{3}{4}(x_2-x_3)^2 f(x1,x2,x3)=x12+x22+x32−x1x2−x1x3−x2x3=(x1−21x2−21x3)2+43x22+43x32−23x2x3=(x1−21x2−21x3)2+43(x2−x3)2;
于是 z 1 = x 1 − 1 2 x 2 − 1 2 x 3 , z 2 = 3 2 ( x 2 − x 3 ) z_1=x_1-\frac{1}{2}x_2-\frac{1}{2}x_3,z_2=\frac{\sqrt{3}}{2}(x_2-x_3) z1=x1−21x2−21x3,z2=23(x2−x3),那如何定义 z 3 z_3 z3呢,其实我们可以随便定义都行,只要使得 Z = P X Z=PX Z=PX中的矩阵P是可逆的就行,比如 z 3 = x 3 z_3=x_3 z3=x3
{ z 1 z 2 z 3 } = { 1 − 1 2 − 1 2 0 3 2 − 3 2 0 0 1 } { x 1 x 2 x 3 } (①) \left\{ \begin{matrix} z_1 \\ z_2\\ z_3 \end{matrix} \right\} = \left\{ \begin{matrix} 1&-\frac{1}{2}&-\frac{1}{2}\\ 0&\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2}\\ 0&0&1 \end{matrix} \right\} \left\{ \begin{matrix} x_1 \\ x_2\\ x_3 \end{matrix} \right\} \tag① ⎩⎨⎧z1z2z3⎭⎬⎫=⎩⎨⎧100−21230−21−231⎭⎬⎫⎩⎨⎧x1x2x3⎭⎬⎫(①)
对于 g ( y 1 , y 2 , y 3 ) = ( y 1 + y 2 ) 2 + y 3 2 g(y_1,y_2,y_3)=(y_1+y_2)^2+y_3^2 g(y1,y2,y3)=(y1+y2)2+y32;令 z 1 = y 1 + y 2 , z 2 = y 3 z_1=y_1+y_2,z_2=y_3 z1=y1+y2,z2=y3 ,那 z 3 z_3 z3呢? 我们可以令 z 3 = y 2 z_3=y_2 z3=y2,当然了我们也可以令 z 3 z_3 z3等于其他的,只要使得变换矩阵是可逆的即可 ( 如果我们令 z 3 = y 3 z_3=y_3 z3=y3,那矩阵的秩就是2,不可逆了)
{ z 1 z 2 z 3 } = { 1 1 0 0 0 1 0 1 0 } { y 1 y 2 y 3 } (②) \left\{ \begin{matrix} z_1 \\ z_2\\ z_3 \end{matrix} \right\} = \left\{ \begin{matrix} 1&1&0\\ 0&0&1\\ 0&1&0 \end{matrix} \right\} \left\{ \begin{matrix} y_1 \\ y_2\\ y_3 \end{matrix} \right\} \tag{②} ⎩⎨⎧z1z2z3⎭⎬⎫=⎩⎨⎧100101010⎭⎬⎫⎩⎨⎧y1y2y3⎭⎬⎫(②)
根据上面的①和②,可以得到
{ 1 − 1 2 − 1 2 0 3 2 − 3 2 0 0 1 } { x 1 x 2 x 3 } = { 1 1 0 0 0 1 0 1 0 } { y 1 y 2 y 3 } \left\{ \begin{matrix} 1&-\frac{1}{2}&-\frac{1}{2}\\ 0&\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2}\\ 0&0&1 \end{matrix} \right\} \left\{ \begin{matrix} x_1 \\ x_2\\ x_3 \end{matrix} \right\}= \left\{ \begin{matrix} 1&1&0\\ 0&0&1\\ 0&1&0 \end{matrix} \right\} \left\{ \begin{matrix} y_1 \\ y_2\\ y_3 \end{matrix} \right\} ⎩⎨⎧100−21230−21−231⎭⎬⎫⎩⎨⎧x1x2x3⎭⎬⎫=⎩⎨⎧100101010⎭⎬⎫⎩⎨⎧y1y2y3⎭⎬⎫
把这个式子记成 P 1 X = P 2 Y P_1X=P_2Y P1X=P2Y,则 X = P 1 − 1 P 2 Y X=P_1^{-1}P_2Y X=P1−1P2Y
我们计算 P 1 − 1 P 2 P_1^{-1}P_2 P1−1P2即可
P 1 − 1 P 2 = { 1 2 2 3 0 1 4 3 0 1 0 } P_1^{-1}P_2= \left\{ \begin{matrix} 1&2&\frac{2}{\sqrt{3}}\\ 0&1&\frac{4}{\sqrt{3}}\\ 0&1&0 \end{matrix} \right\} P1−1P2=⎩⎨⎧10021132340⎭⎬⎫

(1)证明: 要想证明P为可逆矩阵,只需要说明 α \alpha α和 A α A\alpha Aα线性无关即可。
然后题目中说了 α \alpha α不是A的特征向量,所以 α \alpha α和 A α A\alpha Aα线性无关.

(2)题目让求 P − 1 A P P^{-1}AP P−1AP,那除非出现类似于 A P = P B AP=PB AP=PB这样的式子,然后 P − 1 A P = B P^{-1}AP=B P−1AP=B , 所以我们构造这样的式子即可
因为 A P = A ( α , A α ) = ( A α , A 2 α ) = ( A α , 6 α − A α ) AP=A(\alpha,A\alpha)=(A\alpha,A^2\alpha)=(A\alpha,6\alpha-A\alpha) AP=A(α,Aα)=(Aα,A2α)=(Aα,6α−Aα)
然后我们想办法把 ( A α , 6 α − A α ) (A\alpha,6\alpha-A\alpha) (Aα,6α−Aα)写成 P B PB PB的形式,即 ( α , A α ) { 0 6 1 − 1 } (\alpha,A\alpha)\left\{ \begin{matrix} 0&6\\ 1&-1 \end{matrix} \right\} (α,Aα){016−1}
这里 B = { 0 6 1 − 1 } B=\left\{ \begin{matrix} 0&6\\ 1&-1 \end{matrix} \right\} B={016−1}
所以 P − 1 A P = B = { 0 6 1 − 1 } P^{-1}AP=B=\left\{ \begin{matrix} 0&6\\ 1&-1 \end{matrix} \right\} P−1AP=B={016−1}
然后我们可以很快把矩阵 B B B的特征值算出来, λ 1 = 2 , λ 2 = − 3 \lambda_1=2,\lambda_2=-3 λ1=2,λ2=−3; 而矩阵A和矩阵B相似,故而特征值相同,所以矩阵B和矩阵A可以相似对角化 { 2 0 0 − 3 } \left\{ \begin{matrix} 2&0\\ 0&-3 \end{matrix} \right\} {200−3}