【Java数据结构与算法】单调栈的运用思路及相关题解
单调栈
单调栈:栈内元素按单调递增(递减)顺序排列
适用问题
通过使用单调栈我们可以访问到下一个比他大(小)的元素
我们需要通过比较数组前后大小关系来解决问题的适合使用单调栈
代码实现
单调栈保证栈内元素是单调递增(减)的
Stack<Integer> stack = new Stack<>();
int[] nums = new int[]{9, 6, 4, 3, 1, 2, 6, 3};
for (int num : nums) {
//如果栈顶元素小于要放入的元素,就弹出。
while (!stack.isEmpty() && stack.peek() < num) {
stack.pop();
//
}
stack.push(num);
}
经典题目及解题思路
下一个更大元素 I
⭐
给nums1、nums2两个数组,其中nums1是nums2的子集
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。
如果不存在下一个更大元素,那么本次查询的答案是 -1 。
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
思路1:暴力循环 + 把nums2中每个数下一个更大元素存起来
思路2:单调栈 + 把每个数对应更大元素存Map。
单调栈,从右边往左遍历数组,栈顶元素即为下一个比他大的元素。
只有更大的数才会把栈里的数pop出去,然后自己进栈,所以右边比较大的数一定在栈里。
思路2代码实现:
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
Stack<Integer> stack = new Stack<>();
Map<Integer, Integer> map = new HashMap<>();
for(int i = nums2.length - 1; i >= 0; i--) {
while(!stack.isEmpty() && stack.peek() < nums2[i]) {
stack.pop();
}
map.put(nums2[i], stack.isEmpty()? -1 : stack.peek());
stack.push(nums2[i]);
}
for(int i = 0; i < nums1.length; i++) {
nums1[i] = map.get(nums1[i]);
}
return nums1;
}
}
思路3:单调栈,从左往右遍历,只有遇到更大的元素才会pop,pop的时候存map
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
Stack<Integer> stack = new Stack<>();
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < nums2.length; i++) {
while(!stack.isEmpty() && nums2[i] > stack.peek()) {
int tem = stack.pop();
map.put(tem,nums2[i]);
}
stack.push(nums2[i]);
}
for(int i = 0; i < nums1.length; i++) {
nums1[i] = map.containsKey(nums1[i]) ? map.get(nums1[i]) : -1;
}
return nums1;
}
}
每日温度
⭐
题目:给一个气温数组,表示对应天的气温。计算每一天要等几天才会有更高的而温度。
思路1:单调栈,栈从右边开始遍历,比较温度,记录数组下标。栈顶即为更高温度对应的下标。
注意:温度相等也要pop,以保证栈顶元素为更高温度。
法1代码:
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
Stack<Integer> stack = new Stack<>();
int n = temperatures.length;
int[] ret = new int[n];
for(int i = n - 1; i >= 0; i--) {
while(!stack.isEmpty() && temperatures[stack.peek()] <= temperatures[i]) {
stack.pop();
}
ret[i] = stack.isEmpty() ? 0:stack.peek() - i;
stack.push(i);
}
return ret;
}
}
思路2:单调栈,从左往右遍历数组,比较温度,记录数组下标,栈内下标对应温度由顶到低递增。只有碰到更高的温度,栈内元素才会pop,pop的同时更新返回数组。
法2代码:
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
Stack<Integer> stack = new Stack<>();
int n = temperatures.length;
int[] ret = new int[n];
for(int i = 0; i < n; i++) {
while(!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
int index = stack.pop();
ret[index] = i - index;//只有碰到更高的温度,栈内元素才会pop,pop的同时更新返回数组。
}
stack.push(i);
}
return ret;
}
}
下一个更大元素II
⭐⭐
题目: 数组是循环数组。返回每个元素下一个更大的元素。
输入: [1,2,1]
输出: [2,-1,2]
思路:单调栈, 从左往右遍历,栈中存数组下标,栈中元素以数组下标对应数字由顶到低递增。
把数组遍历两遍,右边没有更大元素的就能从左边开始找到。
发现用LinkedList 速度一般更快。
class Solution {
public int[] nextGreaterElements(int[] nums) {
Deque<Integer> stack = new LinkedList<>();
int n = nums.length;
int[] ret = new int[n];
Arrays.fill(ret,-1);
for(int i = 0; i < 2 * n; i++) {
while(!stack.isEmpty() && nums[i % n] > nums[stack.peekLast()]) {
int tem = stack.removeLast();
ret[tem] = nums[i % n];
}
stack.add(i % n);
}
return ret;
}
}
接雨水
⭐⭐⭐
题目: 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
单调栈解法思路:
从左到右,一旦遇到更高的柱子,柱子左边就形成凹槽
所以,用单调栈,从左往右遍历数组,栈内保存下标,栈内元素对应柱子高度由顶到低递增。
碰到更高的就计算一次水量
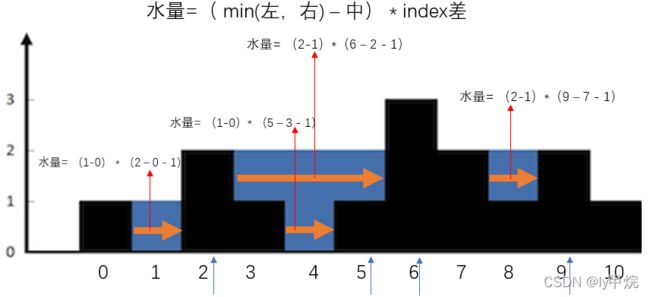
代码实现
class Solution {
public int trap(int[] height) {
Deque<Integer> deque = new LinkedList<>();
int ret = 0;
for(int i = 0; i < height.length; i++) {
//碰到更高的就设法去计算左边的凹槽
while(!deque.isEmpty() && height[i] > height[deque.peekLast()]) {
//凹槽底的高度
int hMid = height[deque.removeLast()];
//找到凹槽左边界
while(!deque.isEmpty() && height[deque.peekLast()] == hMid) {
deque.removeLast();
}
if(deque.isEmpty()) break; //如果是最左边是类似 1 1 2 形状的,就没有水
//凹槽左边界高度
int hL = height[deque.peekLast()];
//凹槽有边界高度
int hR = height[i];
//凹槽左右边界间隔,即水的宽度
int gap = i - deque.peekLast() - 1;
ret += (Math.min(hL, hR) - hMid) * gap;
}
deque.add(i);
}
return ret;
}
}
柱状图中最大的矩形
⭐⭐⭐
题目:给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
思路:单调栈
从左到右,一旦遇到更低的柱子,柱子左边是一个较大的凸包
每次遇到更低的柱子,就尝试计算能组成的最大矩形面积,最后返回所有中最大。
所以,从左往右遍历数组,栈内保存下标,栈内元素对应柱子高度由顶到低递增。
每碰到一个更低的柱子,就尝试去找最大矩形。弹出一个比他大的,依此为左边长,以index差为宽。
index差为,当前位置前一个index - (左边长前一个index + 1) + 1。
直到栈中只剩下比他小的。
过程如下图:
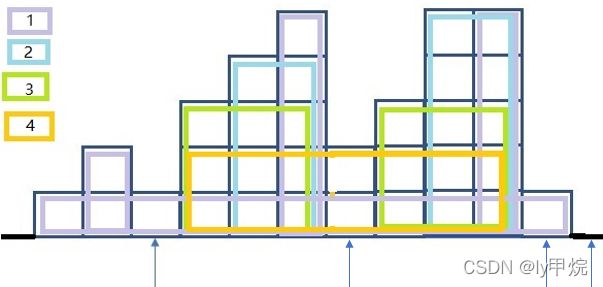
代码实现:
class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
Deque<Integer> deque = new LinkedList<>();
int ret = 0;
for(int i = 0; i <= n; i++) {
//相当于给数组最后补了一个0,用于清算栈中剩余的最小的元素
int tem = i==n ? 0 : heights[i];
//遇到较低的柱子,尝试计算最大矩形,注意这里是while, 每弹出一个就计算以这个为高,以index差为宽的矩形。
while(!deque.isEmpty() && tem < heights[deque.peekLast()]) {
//以弹出的这个柱子为高
int height = heights[deque.removeLast()];
//以弹出柱子为高的最大矩形,其左边对应的index应该为栈顶的那个index + 1
//如果栈顶index + 1 对应的不是弹出柱子,那么它对应的一定是更高的柱子,
//因为如果index + 1 对应的是更低的柱子的话,在之前,此index将会被弹出。
int leftIndex = deque.isEmpty() ? 0 : (deque.peekLast() + 1);
//右边对应的index为当前位置前一个index
int rightIndex = i - 1;
//宽度: 右 - 左 + 1
int width = rightIndex - leftIndex + 1;
ret = Math.max(ret, width * height);
}
deque.add(i);
//System.out.println(deque);
}
return ret;
}
}
最大矩形
⭐⭐⭐⭐
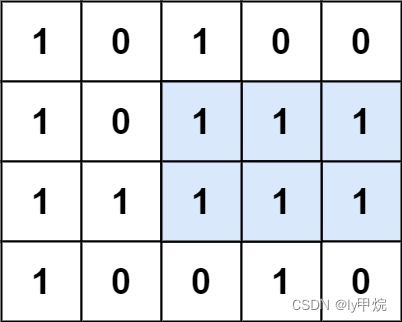
题目:给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:6
解释:最大矩形如上图所示。
思路:
以每行(列)为准,将矩阵按连续的1的个数,转化成为柱状图,来求柱状图最大矩形。
如图所示,以每行为基准,转化柱状图:

只需要找这四个柱状图中最大矩形面积即可。
解题分两步:1.转化为柱状图,2.用单调栈求柱状图最大矩形面积。(遇到更低的柱子,进行计算。)
代码:
class Solution {
public int maximalRectangle(char[][] matrix) {
//按行转化为柱状图
int row = matrix.length, col = matrix[0].length;
int[][] bar = new int[row][col]; //一行代表一个柱状图
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
int height = 0;
int index = i;
while(index >=0) {
if(matrix[index][j] == '1') {
height++;
}else{
break;
}
index--;
}
bar[i][j] = height;
}
}
//System.out.println(Arrays.deepToString(bar));
//求所有柱状图中最大的矩形
int ret = 0;
for(int k = 0; k < row; k++) {
int[] arr = bar[k]; //第 i 个柱状图
Deque<Integer> deque = new LinkedList<>();
//从左往右遍历数组,用单调栈算法,遇到更低的柱子就计算最大的矩阵
for(int i = 0; i <= arr.length; i++) {
int tem = i == arr.length ? 0 : arr[i];
while(!deque.isEmpty() && tem < arr[deque.peekLast()]) {
int height = arr[deque.removeLast()];
int left =deque.isEmpty()? 0 : deque.peekLast() + 1;
int right = i;
ret = Math.max(ret, (right - left) * height);
}
deque.add(i);
}
}
return ret;
}
}
代码优化,
1.求出柱状图立马求出最大矩形,就不需要那么多中间数组变量。
2.求柱状图的时候,下一行的柱状图和上一行是有关系的,如果下一行与上一行对应位置柱状图高度要么为0,要么为上一行的+1.
class Solution {
public int maximalRectangle(char[][] matrix) {
//按行转化为柱状图
int row = matrix.length, col = matrix[0].length;
int[] heights = new int[col]; //一行代表一个柱状图
int ret = 0;
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
if(matrix[i][j] == '1') {
heights[j]++;
}else {
heights[j] = 0;
}
}
ret = Math.max(getMaxArea(heights), ret);
}
return ret;
}
//求所有柱状图中最大的矩形的方法
public int getMaxArea(int[] arr) {
int ret = 0;
Deque<Integer> deque = new LinkedList<>();
//从左往右遍历数组,用单调栈算法,遇到更低的柱子就计算最大的矩阵
for(int i = 0; i <= arr.length; i++) {
int tem = i == arr.length ? 0 : arr[i];
while(!deque.isEmpty() && tem < arr[deque.peekLast()]) {
int height = arr[deque.removeLast()];
int left =deque.isEmpty()? 0 : deque.peekLast() + 1;
int right = i;
ret = Math.max(ret, (right - left) * height);
}
deque.add(i);
}
return ret;
}
}
其他练习题
队列中可以看到的人数
题目: 有 n 个人排成一个队列,从左到右 编号为 0 到 n - 1 ,请你返回数组 answer ,其中 answer[i] 是第 i 个人在他右侧队列中能 看到 的 人数 。
输入:heights = [10,6,8,5,11,9]
输出:[3,1,2,1,1,0]
解释:
第 0 个人能看到编号为 1 ,2 和 4 的人。
第 1 个人能看到编号为 2 的人。
第 2 个人能看到编号为 3 和 4 的人。
第 3 个人能看到编号为 4 的人。
第 4 个人能看到编号为 5 的人。
第 5 个人谁也看不到因为他右边没人。
思路:单调栈,每个人只能看到右边递增的序列,且只能看到一个比自己高的人
从右往左遍历,栈中存的即是右边递增序列(栈顶到栈低), 找到右边递增序列中小于自己的和第一个大于自己的人
代码实现,这里找小于自己及第一个大于自己的人用的一个新的栈暂存数据,来统计
class Solution {
public int[] canSeePersonsCount(int[] heights) {
Deque<Integer> deque = new LinkedList<>();
int n = heights.length;
int[] ret = new int[n];
for(int i = n - 1; i >=0; i--) {
Deque<Integer> tem = new LinkedList<>();
//用一个新的栈,暂存数据并统计个数。
while(!deque.isEmpty()) {
if(deque.peekLast() > heights[i]) {
tem.add(deque.removeLast());
break;
}else {
tem.add(deque.removeLast());
}
}
ret[i] = tem.size();
while(!tem.isEmpty()) {
deque.add(tem.removeLast());
}
//单调栈的实现
while(!deque.isEmpty() && heights[i] > deque.peekLast()) {
deque.removeLast();
}
deque.add(heights[i]);
}
return ret;
}
}
代码优化:
从右往左遍历数组, 栈中存的是右边递增序列,当前位置 i 能看到比它矮的以及第一个比他高的。
那么对于 i - 1 一定看不到 比 i 矮的人。所以栈中不需要存储这些人,即第一次统计完比 i 矮的,直接pop掉就行了。
class Solution {
public int[] canSeePersonsCount(int[] heights) {
Deque<Integer> deque = new LinkedList<>();
int n = heights.length;
int[] ret = new int[n];
for(int i = n - 1; i >=0; i--) {
while(!deque.isEmpty() && deque.peekLast() < heights[i]) {
deque.removeLast();
ret[i]++;
}
//如果pop完以后不为空,那么栈顶的元素一定是大于等于当前元素,只能看到一个
if(!deque.isEmpty()) ret[i]++;
while(!deque.isEmpty() && heights[i] > deque.peekLast()) {
deque.removeLast();
}
deque.add(heights[i]);
}
return ret;
}
}
不同字符的最小子序列/去除重复字母
题目:返回 s 字典序最小的子序列,该子序列包含 s 的所有不同字符,且只包含一次。
输入:s = “leetcode”
输出:“letcod”
题目要求: 1. 去重。2.不能打乱顺序 。3.去重后字典序最小的情况为最终结果。例如:输入:“babc” ,输出:“abc” 而不是"bac"。
字典序升序的子序列一定是最小的子序列。
分析如图所示:
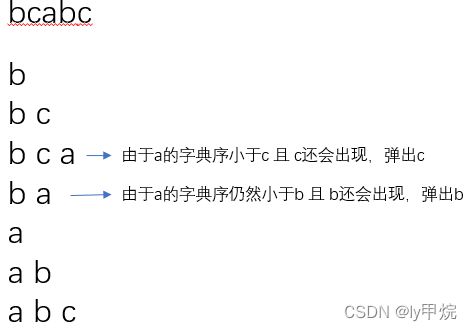
因此运用单调栈的思路,先把数组中各个字母出现的次数进行统计。
从左向右遍历数组,如果当前字母的字母,比栈顶元素的字典序小,且栈顶元素后面还会出现,那么就可以把这个栈顶元素弹出。
核心思想就是 如果已有子序列 ba… 看有没有可能变成 a…b,有可能就把b弹出去。没可能就只能保留 ba继续遍历,栈中出现过的要进行标记,防止重复
代码:
class Solution {
public String removeDuplicateLetters(String s) {
int[] count = new int[26 + 'a'];
char[] arr = s.toCharArray();
int n = arr.length;
//统计字母出现次数
for(char c : arr) count[c]++;
Deque<Character> deque = new LinkedList<>();
boolean[] inStack = new boolean[26 + 'a']; //标记栈中已经存在的元素。
for(int i = 0; i < n; i++) {
count[arr[i]]--;
if(inStack[arr[i]]) continue;
while(!deque.isEmpty() && arr[i] < deque.peekLast() &&count[deque.peekLast()] > 0) {
inStack[deque.removeLast()] = false;
}
deque.add(arr[i]);
inStack[arr[i]] = true;
}
//把栈中元素弄出来并返回。
StringBuilder sb = new StringBuilder();
while(!deque.isEmpty()) {
sb.append(deque.removeLast());
}
return sb.reverse().toString();
}
}