attention与其在RL中的应用

前言

看到新的有趣文章会更新，也欢迎推荐。

attention介绍

attention源于RNN，也就是NLP领域，但是在各个领域都有很大的应用潜力，比如使用self attention的Transformer在各领域开花、甚至成为了通用模型的一部分。

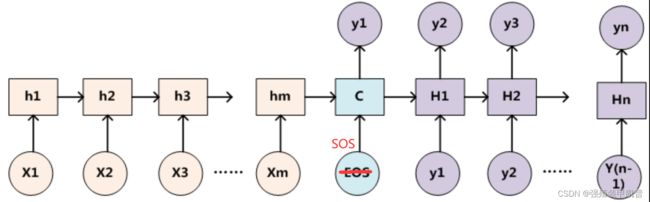
传统Seq2Seq模型使用最后一个输入的隐状态作为语义编码c，也就是解码器的初始隐状态。对于解码器的输入，第一个肯定是SOS，后面的可以只是$y_{i-1}$，也可以是c与$y_{i-1}$的组合，可能需要过一层网络进行特征变换得到合适大小的输入，直至输出EOS或达到最大长度结束（非NLP专业，敬请指正）。虽然decoder看起来有两个输出，但对于RNN来说其只会输出隐状态。

为了区分不同输入对当前输出的重要程度，引入attention机制增强区分度。首先以soft attention为例：

当我们预测$y_i$时，将decoder的隐状态$H_{i-1}$与encoder各个输入对应的隐状态$[h_1,\cdots ,h_m]$对齐，得到source端第j个词对target端第i个词的对齐概率${\alpha }_{ij}$，这是传统机器翻译中的概念：
$${\alpha }_{ij}=align(H_{i-1},h_j)$$
我们可以将其理解为相关性，或是不同source端词对生成target端第i个词的重要性。可以按软寻址理解，即存储器按存储，对于一个query，我们计算不同key的重要程度，然后将value加权求和得到query结果。具体计算分两步，首先是以$H_{i-1}$作为query，$[h_1,\cdots ,h_m]$作为key，计算相关性：
$$e_{ij}=a(H_{i-1},h_j)$$
相关性的计算方式有很多，下面会进行说明。然后通过softmax得到概率：
$${\alpha }_{ij}=\frac{\exp (e_{ij})}{{\sum }_{k=1}^m\exp (e_{ik})}$$
最后就是加权求和得到新的文本向量$c_i$：
$$c_i=\sum _{j=1}^m{\alpha }_{ij}{h}_j$$
其往往与decoder的输入结合，比如拼接和过一层网络。

所谓hard attention就是采样一部分，为了实现梯度的反向传播，需要采用蒙特卡洛采样的方法来估计模块的梯度，应该也可以用gumble softmax。global softmax是使用所有的$h_j$，local softmax则是预测一个source端对齐位置（aligned position）$p_i$，然后基于此选择一个窗口，用于计算文本向量$c_i$。

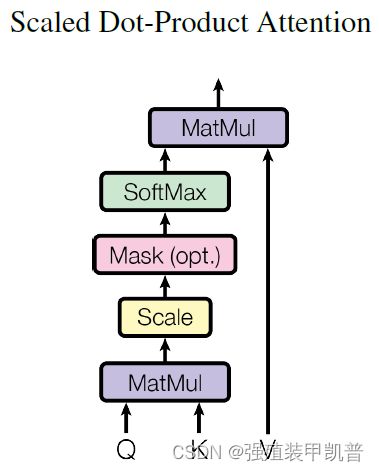
至于self attention则是挖掘自身各元素之间的关系，q、k、v均是source的线性变换：
$$softmax(\frac{Q{K}^{\top }}{\sqrt{d_k}})V$$
可以看出这里使用点积计算相关性。$d_k$是K的维度，保持梯度值稳定，所谓的scale就是这个scaling factor $\frac{1}{\sqrt{d_k}}$，避免梯度消失。

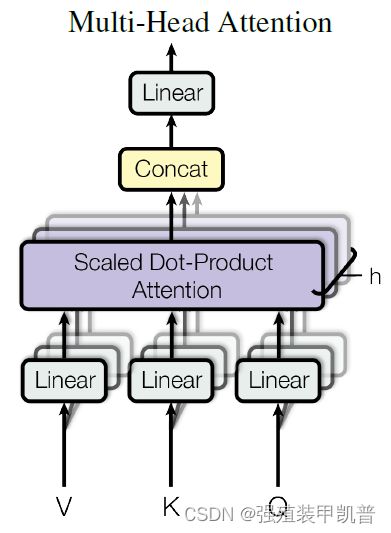
多头则是好几个，最后拼接过线性层。

Self Attention会更容易捕获句子中长距离的相互依赖的特征，因为如果是RNN或者LSTM，需要依次序序列计算，对于远距离的相互依赖的特征，要经过若干时间步步骤的信息累积才能将两者联系起来，而距离越远，有效捕获的可能性越小。但是Self Attention在计算过程中会直接将句子中任意两个单词的联系通过一个计算步骤直接联系起来，所以远距离依赖特征之间的距离被极大缩短，有利于有效地利用这些特征。除此外，Self Attention对于增加计算的并行性也有直接帮助作用。不过self attention失去了序列的顺序信息。

这里主要说明一下权值计算方式：

https://zhuanlan.zhihu.com/p/57501837
https://zhuanlan.zhihu.com/p/37601161
https://zhuanlan.zhihu.com/p/97961666
https://zhuanlan.zhihu.com/p/410776234
https://easyai.tech/ai-definition/attention/

建模观察

[2015.12.5] Deep Attention Recurrent Q-Network

论文链接：https://arxiv.org/abs/1512.01693

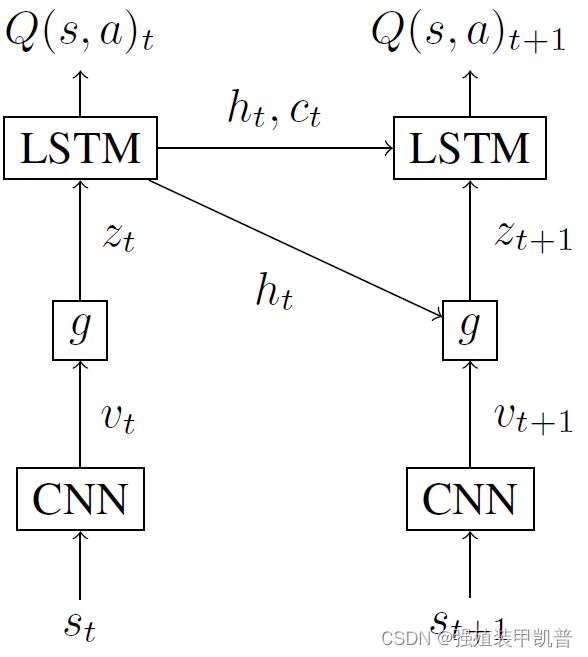
首先是soft attention。状态$s_t$是一个视觉帧，基于此产生D个$m\times m$的feature map，将其转换为一组向量$\{v_t^1,\cdots ,v_t^L\}$，向量长度为D，L=$m\times m$。隐状态$h_t$作为query，找到基于历史信息，在当前时间步应该关注哪些特征。attention模块g是两层全连接网络，计算方式为：

Z是标准化常量，最后加权求和：

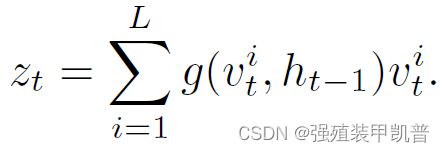
从代码实现来看，Q值是$h_t$经过一层全连接网络得到的。

soft attention在部分场景效果好。hard attention从L个向量中只采样一个，效果相对较差，这里忽略。

[ICML2016] Control of Memory, Active Perception, and Action in Minecraft

论文链接：https://arxiv.org/abs/1605.09128

通过两个矩阵对观察进行变换，跟self attention一样，得到k、v。读时跟带attention的seq2seq的解码器一样，隐状态作为query，软寻址。

Memory Q-Network (MQN)直接使用当前的观察作为query，$h_t=W_c{e}_t$，其中$e_t$是CNN的输出。
Recurrent Memory Q-Network (RMQN)使用LSTM，就是正常带attention的decoder：$[h_t,c_t]=LSTM(e_t,h_{t-1},c_{t-1})$
Feedback Recurrent Memory Q-Network (FRMQN)将上一时刻的读的结果和$e_t$拼接起来作为输入：$[h_t,c_t]=LSTM([e_t,o_{t-1}],h_{t-1},c_{t-1})$

Q网络输入的是$(h_t,o_t)$，跟DRQN和DARQN一致。

FRQMN效果很好，泛化性很强。

[ICLR 2019] Relational Deep Reinforcement Learning

论文链接：https://arxiv.org/abs/1806.01830

跟DARQN状态类似，也是多个feature map，作者假设每个point就是entity，每行是一个entity，堆叠成矩阵，进行多头attention，建模entity之间的关系，这是一个relational block。这个过程可以进行多次，参数共享的是recurrent，不共享的是deep。

能学习可解释的策略，在样本效率、泛化能力和整体表现都有提高。

[NIPS2018] Relational recurrent neural networks

论文链接：https://arxiv.org/abs/1806.01822

相当于对LSTM进行了魔改，将cell变成的memory，其余基本一致，得到推理能力。

首先是对memory的处理，一开始可以随机初始化一个memory矩阵，每行是一条memory。然后每个时间步，将当前的输入按行拼接，拼接后的矩阵计算k、v，拼接前的计算q，按照self attention的方式得到更新后的memory，这就是图中模块A的作用：

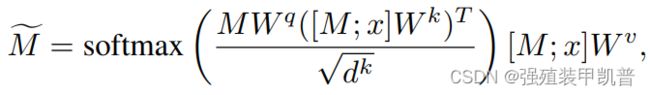
然后与$\tilde{M}+M=M^{\prime }$，过MLP得到$M^{\prime \prime }$，然后$M^{\prime }+M^{\prime \prime }=\hat{M}$，对memory的处理完毕，形状是[memory_slots, memory_size]。虽然看起来这样q和k、v来自不同变量，但可以直接用[M;x]做self attention，假设x有n行，把最后结果里的倒数n行去掉即可。

下面是 gating 部分，input过一层MLP变成 memory_size，记做$x_t$，整体流程与LSTM基本一致，只有cell状态变成了memory：

可以看出$x_t$要跟memory中的每一条运算，看代码https://github.com/L0SG/relational-rnn-pytorch时会困惑维度不一样它怎么没用repeat成memory_slots，原来在relational_rnn的create_gates函数里通过gates = gate_memory + gate_inputs自动repeat了，太细了。最后$h_t$的size为[batch, memory_slots*memory_size]。

在多个场景下都提升了效果，作者认为是明确建模记忆交互的结果。

[GECCO2020] Neuroevolution of Self-Interpretable Agents

论文链接：https://arxiv.org/abs/2003.08165

人类选择性的注意力会忽视一些东西，作者利用这个消除环境中无用的干扰。

前期跟DRRL一样，都是一样的状态处理，不过通过q、k得到attention矩阵后，每行是以这个patch为query，其他patch对他的重要性，作者将其理解为该patch对其他patch的投票，按行相加相当于计票得到importance vector，然后选top k的patch作为观察进行决策。

效果好，移除特征可以缩小模型，环境微小改动时泛化性很好，但是变化大的时候不行，可以适当增大k缓解。

[AAAI2017] Multi-focus Attention Network for Efficient Deep Reinforcement Learning

论文链接：https://arxiv.org/abs/1712.04603

作者认为不能直接输入low-level的感知，而是应该利用entity间的联系。

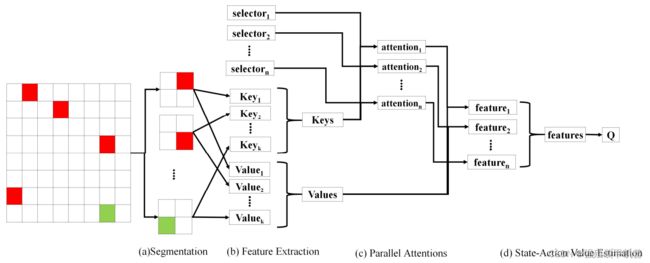
首先对输入进行分割，作者这里输入是图像，就直接分成多个patch了，也就是局部特征。

然后是特征提取，假设$c_i$是第i个局部状态的特征，作者通过卷积和MLP得到，并拼接了局部特征的index。根据其计算k、v，$k_i=W_k{c}_i$，$v_i=f_v(W_v{c}_i)$，$f_v$是leaky ReLU。

接着是attention，有N个，类似多头。selector $a_n$是可学习的向量，用作q，第n个attention产生的权重向量中第i个元素的计算方式为：
$$A_i^n=\frac{\exp (a_n{k}_i^{\top })}{{\sum }_{i^{\prime }}\exp (a_n{k}_{i^{\prime }}^{\top })}$$
$i^{\prime }$是除i外的所有局部特征，这里我不太理解，因为按理说softmax底下的求和不该去掉i。为了避免不同$a_n$变得相似，从而注意不同的方面，作者加了正则项：

$R_e$是熵正则，熵越大权重越不一样。$R_d$是距离正则，越小越不一样。但作者实验中发现正则项没用，随机初始化已经足够了。

最后是Q值计算，每个attention的权重与v加权求和都能得到对应的$h_n={\sum }_i{h}_i^n{v}_i$，拼接后$[h_1,\cdots ,h_N]$计算Q值。

作者还将其扩展到协作局部可观察多智能体通信场景，与单智能体区别在于：feature extraction时，$a_i=W_a{c}_i$，确保每个智能体的不一样；parallel attentions变成了attentive communication：
$$A_j^i=\frac{\exp (a_i{k}_j^{\top })}{{\sum }_{j^{\prime }}\exp (a_i{k}_{j^{\prime }}^{\top })}$$
即智能体i对j的注意程度，j包括i，按理说$j^{\prime }$也应该包括j。至于Q值计算，需要通信信息$h_i={\sum }_j{h}_j^i{v}_j$和智能体自己的信息$v_i$，拼接后$[h_i,v_i]$计算。作者发现实验中容易发散，加了正则项限制：
$$R=\lambda (a\cdot k^{\top })$$

在单智能体场景下加速训练、提升效果。多智能体场景加速了训练，但因为baseline也达到最优了，难以评价效果提升。主要特点在于q是一个可学习变量。

建模关系

[ICML2019] Actor-Attention-Critic for Multi-Agent Reinforcement Learning

论文链接：https://arxiv.org/abs/1810.02912

上面是critic的架构，可以看出和MADDPG类似，都是集中式的，区别在于多了soft attention。

智能体自己的状态和动作经过一层MLP得到$e_i$，然后自己的作为q，其他的作为k、v进行query。其中v经过共享矩阵V的线性变换后还经过leaky ReLU，然后权值计算类似self attention，同样可以进行多头，最后直接拼接。智能体间共享权重矩阵鼓励共同的embedding空间，作者认为critic参数也可以共享，因为多智能体值函数近似本质上是多任务回归，奖赏对于个体智能体不同但有共同的特征，学习会高效。

critic最小化有熵的损失促进探索：

actor做梯度上升：

b是baseline。对于离散动作，可以输出所有动作的Q值，然后根据概率算期望，这样输入中就不能有$a_i$，类似基于值的方法，别人也是这么实现的。对于连续动作，原文是“either estimate the above expectation by sampling from agent i’s policy, or by learning a separate value head that only takes other agents’ actions as input”，我不是很理解，我觉得应该输出正态分布的均值和方差吧。对于其他智能体的动作，作者没有像MADDPG一样选择样本中的，认为这会造成overgeneralization，使得智能体不能与其他智能体的当前策略协作，因此根据样本观察重新生成动作。

效果很好，尤其是在依赖其他智能体的场景下。

[AAAI2020] Multi-Agent Game Abstraction via Graph Attention Neural Network

论文链接：https://arxiv.org/abs/1911.10715

首先，智能体i与智能体$j\ne i$的embedding组合后$(h_i,h_j)$放入双向LSTM避免顺序依赖，然后经过gumble softmax得到hard attention $w_h^{i,j}$。

然后是soft attention：
$$W_s^{i,j}\propto \exp (h_j^{\top }{W}_k^{\top }{W}_q{h}_i{W}_h^{i,j})$$
这里我觉得应该把$W_h^{i,j}$为0的直接去掉，不参与soft attention，因为softmax之后还是会给他们权重。

作者基于G2ANet提出了新的通信方法。智能体使用LSTM，类似DRQN。经过两层attention后得到两种权重，最后所谓的GNN就是加权求和：
$$x_i=\sum W_h^{i,j}{W}_s^{i,j}{h}_j$$
然后基于$(x_i,h_i)$得到动作。这里可以看出计算时还是乘以了$W_h^{i,j}$，那么去掉$W_h^{i,j}=0$的$j$后，$W_s^{i,j}$和不为1，我觉得是有问题的。

还提出了AC架构的，不过与MAAC类似，包括$e_i,x_i$的含义，区别在于计算$x_i$时多了一层hard attention。

效果都挺好的。

[AAMAS2020] Learning Transferable Cooperative Behavior in Multi-Agent Teams

论文链接：https://arxiv.org/abs/1906.01202

文章解构多智能体环境，从黑盒建模为agent-entity图，即将智能体和实体看做点，边代表彼此之间有通信，对智能体数目和排列变化都不变。在一个episode中，点保持静止，但不同episode可以随机变化。作者考虑距离的受限通信和不受限通信。关系跟观察都建模了，由于建模观察部分与DRRL类似，因此放在建模关系里。

每个智能体只能观察到自己的局部状态$X^i$，包括位置和速度，然后得到环境编码$U^i=f_a(X^i)$。对于环境的实体$l$，首先得到embedding $e_i^l=f_e(X_i^l)$，其中$X_i^l$是相对状态。然后通过self attention更新$e_i^l$，作者称这个过程为entity message passing，最后整合成固定大小的环境embedding $E^i$。然后将$U^i$和$E^i$拼接变成$h^i$，代表智能体对自己状态和环境的理解。

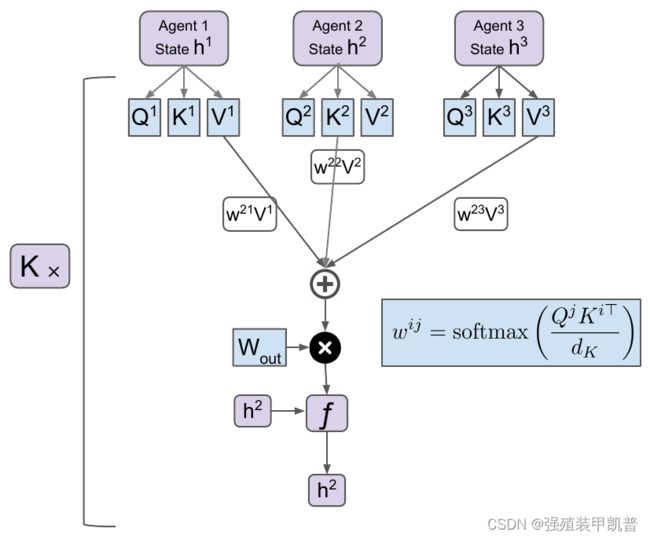
然后用共享的矩阵$W_Q,W_K,W_V$计算q、k、v，用自己的作为q，query其他智能体（包括自己），进行self attention，加权求和后通过$W_{out}$线性变换得到$V_f^i$，然后与$h^i$拼接后进行非线性变换得到新的$h^i$。并且可以进行多跳通信，也就是重复K轮，使得不直接相连的智能体也能通信，实验中为3。总的来说有点像DRRL进行环境编码，然后self attention进行通信。作者使用PPO实现，并且认为通信也是decentralized。

效果很好，并且EMP要比单纯把实体向量拼接效果好，特别是智能体数目多的场景，增加观察空间的大小导致需要更多的样本。Zero shot Generalization中，受限通信会更好。

[ICLR2020] Graph Convolutional Reinforcement Learning

论文链接：https://arxiv.org/abs/1810.09202

这个DGN跟上面那个类似，从arxiv的提交时间看这篇提交更早，但上面那个发表更早。DGN在相关工作里说上面那个要显式地label环境里的实体，现实应用中不可行。我觉得有点太死板了吧，明明智能体通信的做法几乎是一样的，大概这就是学术的严谨性吧。跟MAAC也相似，不过MAAC是soft attention，并且只有一轮，论文里也没提。

每次卷积就是进行一次多头attention，相当于把DRRL的relational kernel搬过来，其实跟上面那个相比也就多了多头。每层卷积的输出都保留，最后拼接。作者认为协作是持续并且长期的，因此attention权重应该稳定，作者固定相邻两个时间步的邻接矩阵，使用当前的网络产生当前的权重和下一个时间步的权重，然后通过KL散度进行约束，不使用目标网络是因为延迟更新导致关系不一致。

m是头，k是卷积层，$\lambda =0.03$，作者认为上层的应该更抽象更稳定，因此约束上层卷积产生的权重。

实验使用DQN，正则项有一点作用，多层卷积很有用。

From Few to More: Large-scale Dynamic Multiagent Curriculum Learning
论文链接：https://arxiv.org/abs/1909.02790

[2020.6.9] Qatten: A General Framework for Cooperative Multiagent Reinforcement Learning

论文链接：https://arxiv.org/abs/2002.03939

严格来说可能不算attention，设计上没有q、k、v，只是借用这个结构。作者先通过推导得到$Q_{tot}$与$Q^i$之间的关系：
$$Q_{tot}(s,\text{a})\approx c(s)+\sum _{i,h}{\lambda }_{i,h}(s)Q^i(s,a^i)$$
然后借助soft attention的结构实现：

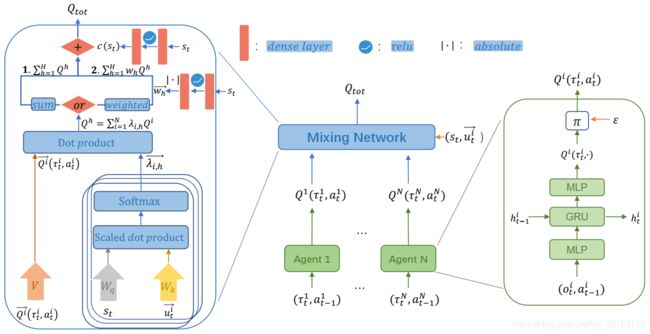
用多头表示多阶。效果挺好的，但在单向MMDP上发现其难以收敛到真实Q值。