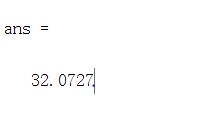吴恩达-机器学习系列课程-Matlab作业

欢迎批评指正

ex1 Linear Regression

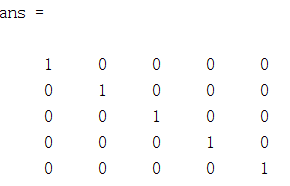
warmUpExercise.m

A=eye(5);

结果：

plotData.m

figure; % open a new figure window

plot(x, y, 'rx', 'MarkerSize', 10); % Plot the data
ylabel('Profit in $10,000s'); % Set the y-axis label
xlabel('Population of City in 10,000s'); % Set the x-axis label

r:red
x:x-shapped point
MarkerSize:point size
结果：

computeCost

h = X*theta;
J = 1/(2*m)*sum((h-y).^2);
实数矩阵转置：'
矩阵每个元素平方:.^

结果：

gradientDescent

    h = X*theta;
    theta = theta-alpha/m*X'*(h-y);
    % theta has two vars, X doesnt have to only take secth col

结果：

feature normalization

mu = mean(X, 1);
sigma = std(X, 0, 1);
for i = 1:size(X, 2)
    X_norm(:,i) = (X_norm(:,i)-mu(1, i))/sigma(1, i);
end
%mean(X, 1/2) return X matrix cols/rows mean
%std(X, 0/1, 1/2) return X matrix cols/rows 标准差
%0 stand for n-1
%1 stand for n
% X_norm(:,i)-mu(1, i) work for all rows

computeCostMulti

h = X*theta;
J = 1/(2*m)*sum((h-y).^2);
%computCost still work here

结果

gradientDescentMulti

    h = X*theta;
    theta = theta - alpha/m*((h-y)'*X)';

结果：

normalEqn

theta = pinv(X' * X) * X' * y;
% pinv return inverse of a matrix

ex2 Logistic Regression

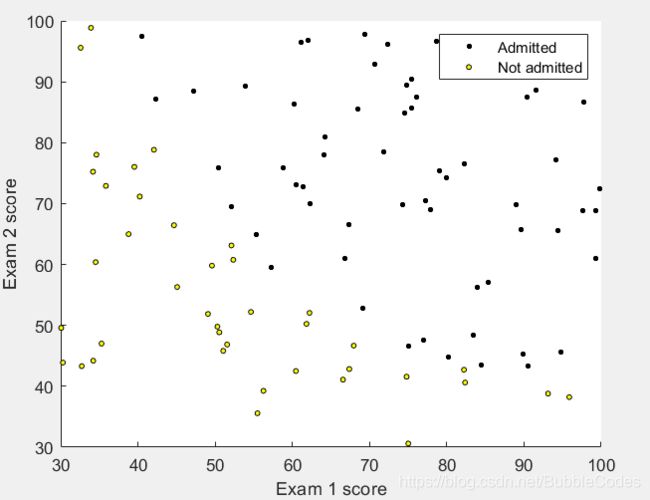
plotData

% Find Indices of Positive and Negative Examples
pos = find(y==1); neg = find(y == 0);
% Plot Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, 'MarkerSize', 3);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', 'MarkerSize', 3);
%find:return the index of element(according to the col)

结果：

sigmoid

g = 1./(1+exp(-z));
% 1/[1, 2] == error
% 1./[1, 2] == [1, 0.5]
% f=@(h) 1 ./ (1 + exp(-h)); % 1 / (1 + exp(-h));
% g = f(z);

costFunction

h = sigmoid(X*theta);
J = 1/m*(-y'*log(h)-(1-y')*log(1-h));
grad = 1/m*X'*(h - y);

结果：

predict

p = round(sigmoid(X*theta));
% round: return the closest integer
% p is the predict, not the probablity

结果：

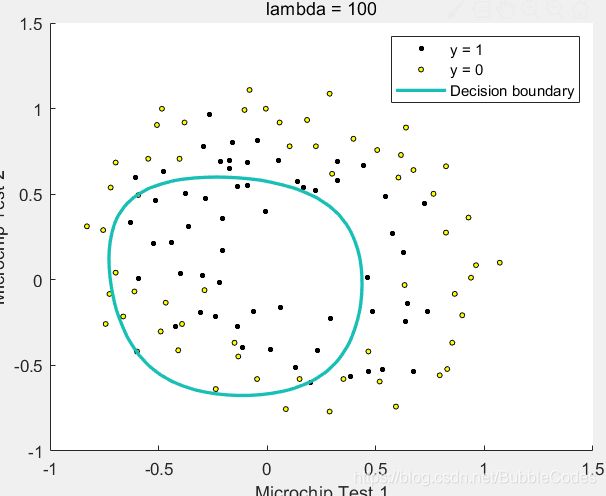
costFunctionReg

h =sigmoid(X*theta);
theta_1=[0;theta(2:end)]; % theta_0不需要正则化
J = 1/m*(-y'*log(h)-(1-y')*log(1-h))+lambda/(2*m)*sum(theta_1.^2);
grad = 1/m*X'*(h - y) + lambda/m*theta_1;

结果：

ex3 Multi-class Classification and Neural Networks

LrCostFunction

h = sigmoid(X*theta);
thetaZero = theta;
thetaZero(1) = 0;
J = 1/m*(-y'*log(h)-(1-y)'*log(1-h))+lambda/(2*m)*sum(thetaZero.^2);
grad = 1/m*X'*(h-y)+lambda/m*thetaZero;
% theta(1) = theta_0, who doesnt need to regularization

结果：

oneVsAll

% Set Initial theta
initial_theta = zeros(size(all_theta, 2), 1);

% set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 50);
% iterat 50

for i = 1 : num_labels
    theta = fmincg(@(t)(lrCostFunction(t, X, (y==i), lambda)), initial_theta, options);
    all_theta(i,:) = theta;
end
% y==i has the same size with y

如何利用fminunc、f优化函数来求参数的值：

结果：

predictOneVsAll

h = all_theta*X';
[max_val, max_index] = max(h, [], 1);
p = max_index';
% 1 represents the output is 1*n
% 2represents the output is n*1

结果：

predict

%
for i = 1:m
    X_1 = [1 X(i, :)];
    Z1 = Theta1*X_1';
    A1 = sigmoid(Z1);

    A1 = [1 A1'];
    Z2 = Theta2*A1';
    A2 = sigmoid(Z2);
    
    [max_val ,p(i)] = max(A2);
end

结果：

ex4 Neural network learning

nnCostFunction(Feedforward and cost function)

%recode y 
y1 = zeros(num_labels, m);
for i = 1:m
    y1(y(i), i) = 1;
end

%1th layer
A1 = [ones(size(X, 1), 1) X];

%2th layer
Z2 = Theta1*A1';
A2 = sigmoid(Z2);
A2 = [ones(1, size(A2, 2)); A2];

%3th layer
Z3 = Theta2*A2;
A3 = sigmoid(Z3); %K*m

J = 1/m*sum(sum(-log(A3).*y1-log(1-A3).*(1-y1)));
% nots:
%we get the prediction A3 which is a K*m matrix
%each col is the prediction of each classifier
%so we need to recode y to get each cost of each classifier of every example.
%now, we only get the costFunction J not dJ/dθ

结果：

nnCostFunction (Regularized cost function)

%recode y 
y1 = zeros(num_labels, m);
for i = 1:m
    y1(y(i), i) = 1;
end

%1th layer
A1 = [ones(size(X, 1), 1) X];

%2th layer
Z2 = Theta1*A1';
A2 = sigmoid(Z2);
A2 = [ones(1, size(A2, 2)); A2];

%3th layer
Z3 = Theta2*A2;
A3 = sigmoid(Z3); %K*m

%unregularizatied
J = 1/m*sum(sum(-log(A3).*y1-log(1-A3).*(1-y1)));

%regularization
regPart = lambda/(2*m)*(sum(sum(Theta1(:, 2:size(Theta1, 2)).^2)) + sum(sum(Theta2(:, 2:size(Theta2, 2)).^2)));
J = J+regPart;
%note:
%??Theta1/2(0) for each classifier are not in regularization part.

结果：

sigmoidGradient

g = sigmoid(z).*(1-sigmoid(z));
%mind the .*

结果：

randInitializeWeights(Random initialization)

%Randomly initialize the weights to small values
epsilon_init = 0.12;
W = rand(L_out, 1 + L_in) * 2 * epsilon_init - epsilon_init;
% rand(x, y) returns a x*y matrix which follows Uniform distribution

无结果

nnCostFunction(Backpropagation)

%--------------------------------------------------
%forward propagation
%recode y 
y1 = zeros(num_labels, m);
for i = 1:m
    y1(y(i), i) = 1;
end

%1th layer
A1 = [ones(size(X, 1), 1) X];%m*(layer1_size+1)
A1 = A1';%(layer1_size+1*m)

%2th layer
Z2 = Theta1*A1;
A2 = sigmoid(Z2);
A2 = [ones(1, size(A2, 2)); A2];

%3th layer
Z3 = Theta2*A2;
A3 = sigmoid(Z3); %K*m

%unregularizatied
J = 1/m*sum(sum(-log(A3).*y1-log(1-A3).*(1-y1)));

%regularization
regPart = lambda/(2*m)*(sum(sum(Theta1(:, 2:size(Theta1, 2)).^2)) + sum(sum(Theta2(:, 2:size(Theta2, 2)).^2)));
J = J+regPart;

%-----------------------------------------------------------------------
%backpropagation
%size(X) = m*1thLayer
%size(a1) = 1thLayer*m
X = X';
for i = 1:m
    %1th layer
    %size(a1) = lthLayer*1
    a1 = X(:, i);
    
    %2th layer
    %size(Theta1) = 2thLayer*(1thLayer+1)
    %size(a2) = size(z2) = 2thLayer*1
    z2 = Theta1*[1; a1];
    a2 = sigmoid(z2);
    
    %3th layer
    %size(Theta2) = 3thLayer*(2thLayer+1)
    %size(a3) = 3thLayer*1
    z3 = Theta2*[1;a2];
    a3 = sigmoid(z3);
    
    %error back propagation
    %there is no delta1
    %size(delta3) = 3thLayer*1
    %size(delta2) = 2thLayer*1
    %size(Theta2) = 3thLayer*(2thLayer+1)
    delta3 = a3-y1(:, i);
    delta2 = Theta2(:, 2:size(Theta2,2))'*delta3.*sigmoidGradient(z2);
    
    %size(Theta2_grad) = size(Theta2) = 3thLayer*(2thLayer+1)
    %size(Theta1_grad) = size(Theta1) = 2thLayer*(1thLayer+1)
    %size(delta3) = 3thLayer*1
    %size(delta2) = 2thLayer*1
    %size(a2) = 2thLayer*1
    %size(a1) = 1thLayer*1
    
    Theta2_grad = Theta2_grad + delta3 * ([1; a2]');
    Theta1_grad = Theta1_grad + delta2 * ([1; a1]');
end

%size(Theta2_grad) = size(Theta2) = 3thLayer*(2thLayer+1)
%size(Theta1_grad) = size(Theta1) = 2thLayer*(1thLayer+1)
Theta1_grad(:, 1) = Theta1_grad(:, 1)./m;
Theta2_grad(:, 1) = Theta2_grad(:, 1)./m;
Theta1_grad(:, 2:end) = Theta1_grad(:, 2:end)./m+lambda/m.*Theta1(:, 2:end);
Theta2_grad(:, 2:end) = Theta2_grad(:, 2:end)./m+lambda/m.*Theta2(:, 2:end);

结果：

ex5 Regularized Linear Regression and Bias v.s. Variance

linearRegCostFunction

h = X*theta;
J = 1/(2*m)*sum((h-y).^2)+lambda*sum(theta(2:end, :).^2)/(2*m);
grad = 1/m*X'*(h-y)+lambda/m*[0;theta(2:end, :)];

结果:

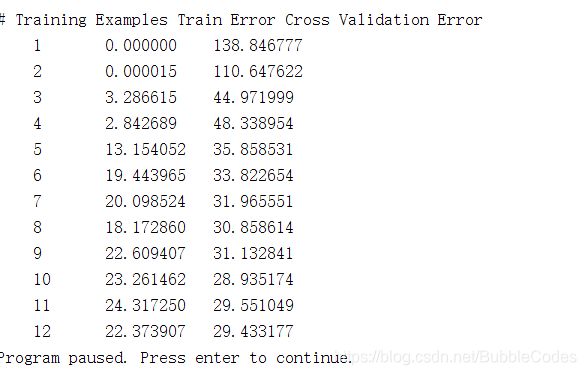
learningCurve

for i = 1:m
   theta_i = trainLinearReg(X(1:i, :), y(1:i, 1), lambda);
   [error_train(i, 1), grad_train] = linearRegCostFunction(X(1:i, :), y(1:i, 1), theta_i, 0);
   [error_val(i, 1), grad_val] = linearRegCostFunction(Xval, yval, theta_i, 0);
end
% need to notice:
% 1:when computing the error, lambda = 0,  which means that no regularization term in error.
% 2:when computing the error_val, you need count all the cross validation set in
%high bias problem exits

结果：

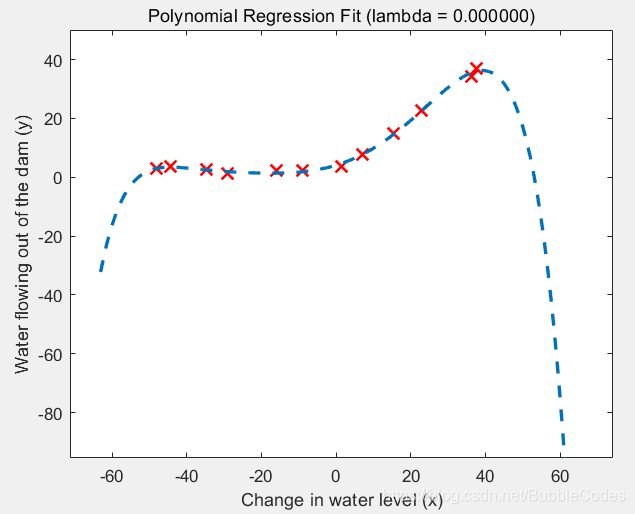
polyFeatures

for i = 1:p
   X_poly(:, i) = X(:, 1).^i; 
end
%low bias
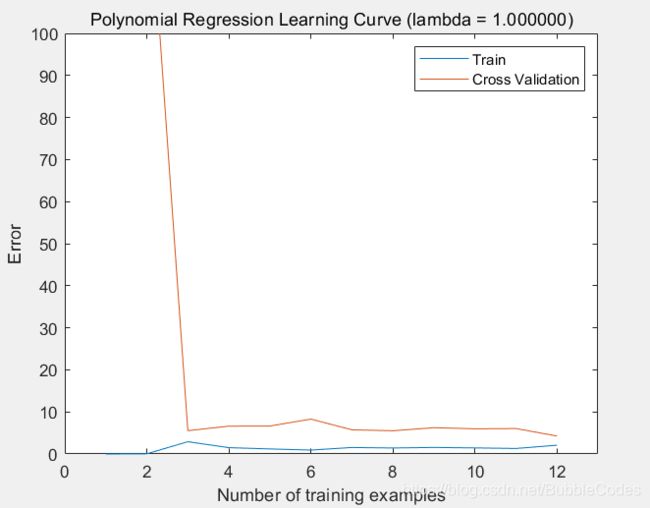
%high variance. There is a gap between the training and cross validation errors, indicating a high variance problem.
%解决方法是引入regularization

结果：

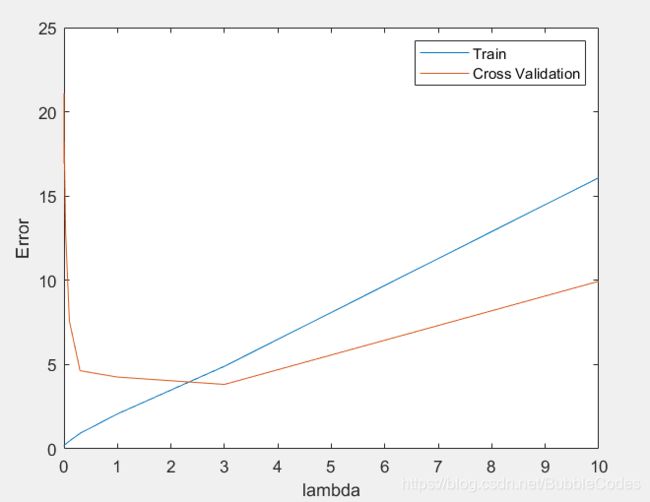
validationCurve

for i = 1:length(lambda_vec)
    theta = trainLinearReg(X, y, lambda_vec(i));
    [error_train(i), grad_train] = linearRegCostFunction(X, y, theta, #pic_center);
    [error_val(i), grad_val] = linearRegCostFunction(Xval, yval, theta, 0);  
end
% visualize the effect of lambda

结果：

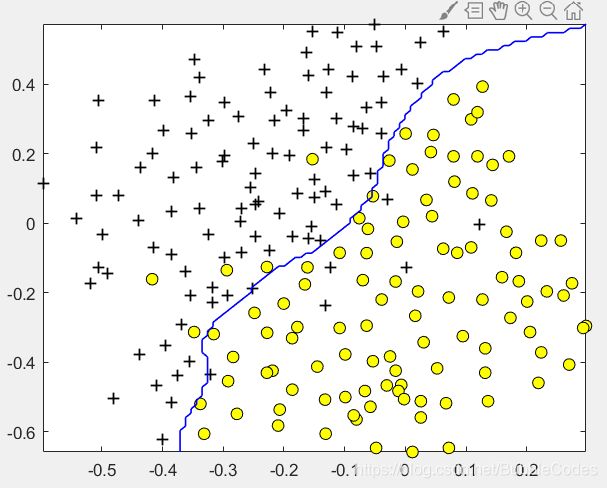
ex6 Support Vector Machines

gaussianKerne

sim = exp(-sum((x1-x2).^2)/(2*sigma^2));

结果：

dataset3Params

testValues = [0.01, 0.03, 0.1, 0.3,  1, 3, 10, 30];
results = [];

for loopC = 1:length(testValues)
    for loopSigma = 1:length(testValues)
      testC = testValues(loopC);
      testSigma = testValues(loopSigma);
      
      model= svmTrain(X, y, testC, @(x1, x2) gaussianKernel(x1, x2, testSigma)); 
      predictions = svmPredict(model, Xval);
      
      testError = mean(double(predictions ~= yval));
      
      fprintf("C: %f\nsigma: %f\nerror: %f\n", testC, testSigma, testError);
      
      results = [results; testC, testSigma, testError];
    end
end

[minError, minIndex] = min(results(:,3));

C = results(minIndex,1);
sigma = results(minIndex,2);

fprintf("\n\nLeast error:\nC: %f\nsigma: %f\nerror: %f\n", C, sigma, minError);
%关于~=在矩阵中的应用：
%其相当于≠
%作用与两个相同size的矩阵时，对应位置相等的地方填逻辑0，不相等的地方填逻辑1

结果：

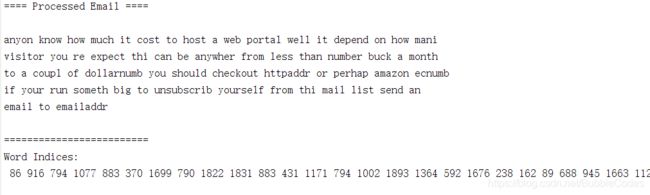
processEmail

% find(判断)：返回满足条件的元素下标
%ismember判断是否为其元素
word_indices = [word_indices; find(ismember(vocabList, str))];

结果：

emailFeatures

x(word_indices)=1;
%X向量与vocabList向量维度大小一致
%letter中出现了某单词，即将X向量对应位置置一

ex7 K-means Clustering and Principal Component

Analysis

findClosestCentroids

for i = 1:size(X, 1)
   distances = sum((X(i, :).*ones(size(centroids)) - centroids).^2, 2);
    [minValues, idx(i)] = min(distances, [], 1); 
end
% 对每个样本，计算其到每个聚类中心的距离

结果：

computeCentroids

for i = 1:K
   rowIndex = find(idx == i);
   if size(rowIndex, 1) > 0
       centroids(i, :) = 1/length(rowIndex) * sum(X(rowIndex, :) , 1);
   end
end
% need to judge whether there is miu_k that has samples attributed

结果：

pca(Principle Component Analysis)

% computing the covariance matrix of data X
sigma_capital = 1/m .* X'*X;

% computing the eigenvector of sigma_capital
% where U will contain the principal components and S will contain a diagonal matrix
[U, S, V] = svd(sigma_capital);

结果：

% U is n*n, U_reduce is n*K
U_reduce = U(:, 1:K);

% Computing the projection of each sample on each vector*K(1*n)
Z = X*U_reduce;

结果：

recoverData

% why?
U_reduce = U(:, 1:K);
X_rec = Z*U_reduce';

结果：

ex8 Anomaly Detection and Recommender Systems

estimateGaussian

mu = mean(X, 1);
sigma2 = var(X, 0, 1);

结果：

selectThreshold

    % caculate truePostive, falsePostive, falseNegtiive
    % & used between matrix, && used between scalar. same with | and ||
    tp = length(nonzeros((pval < epsilon) & (yval == 1)));
    fp = length(nonzeros((pval < epsilon) & (yval == 0)));
    fn = length(nonzeros((pval > epsilon) & (yval == 1)));
    
    % caculate the precsion, recall, F1
    prec = tp/(tp+fp);
    rec = tp/(tp+fn);
    F1 = 2*prec*rec/(prec+rec);

结果：

cofiCostFunc

% regularization term
J = 1/2 * sum( ( (X * Theta' - Y).*(R==1) ).^2 , 'all') + lambda/2*sum(sum(X.^2)) + lambda/2*sum(sum(Theta.^2));

% gradient term without regularized
X_grad = (X * Theta' - Y) .* (R==1) * Theta;
Theta_grad = ((X * Theta' - Y).*(R==1))' * X;

% regularization term
% X_grad is nm*n
% Theta_grad is nu*n
X_grad = X_grad + lambda.*X;
Theta_grad = Theta_grad + lambda.*Theta;

结果：

…