李宏毅机器学习作业二

前言

第二个作业是年收入判断，任务是做一个线性二元分类器，根据人们的个人资料来判断其年收入是否高于50000美元。这里用了逻辑回归和概率生成模型两种方法。

 

 

数据集有X_train,Y_train,X_test三个文件。这三个文件是老师事先帮我们将数据整理成csv格式并且全都是数字的数据。

X_train、 X_test ：每一行包含一个510-dim的特征，代表一个样本。

Y_train: label = 0 表示 "<=50K" 、 label = 1 表示 " >50K " 。
训练数据共54256个

测试集大概20000多个

参数共510个。

那么可以得出结论：

模型的输入是510维

模型输出是一个布尔值表示预测的是或不是。

        上课共讲了两种方法，一种是逻辑回归，一种是生成模型。只不过生成模型的w和b是通过平均值和协方差直接求出来，而不需要梯度下降进行收敛获得。具体步骤和用到的Normalize函数和分类函数都一样。

逻辑回归方法

逻辑回归：

1.数据准备

2. 一些有用的函数

3.梯度与损失

4.模型训练

5.绘制损失和精度曲线

6.预测测试标签

一.数据准备

把csv文件解析为numpy数组，据分别存入X_train，Y_train,X_test中

import numpy as np

np.random.seed(0)
X_train_fpath = './X_train.csv'
Y_train_fpath = './Y_train.csv'
X_test_fpath = './X_test.csv'
output_fpath = './output_{}.csv'

with open(X_train_fpath) as f:
    next(f)
    X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype=float)
    #line.strip(’\n’) 移除换行符并返回列表。split()通过指定分隔符对字符串进行切片。line.strip(’\n’).split(’,’) 通过逗号进行切片。
with open(Y_train_fpath) as f:
    next(f)
    Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype=float)
with open(X_test_fpath) as f:
    next(f)
    X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype=float)

对数据进行标准化并划分训练集和验证集的函数定义

def _normalize(X, train=True, specified_column=None, X_mean=None, X_std=None):
    if specified_column == None:        # 如果等于None的话，意味着所有列都需要标准化
        specified_column = np.arange(X.shape[1])       # 新建一个数组，是0-X.shape[1]即0-509
    if train:    # 如果train为True，那么表示处理training data，否则就处理testing data,即不再另算X_mean和X_std
        X_mean = np.mean(X[:, specified_column], 0).reshape(1, -1)
        # 对X的所有行以及特定列的数组中求各列的平均值（因为axis的参数为0），然后重组为一行的数组
        X_std = np.std(X[:, specified_column], 0).reshape(1, -1)
        # 同X_mean
    X[:, specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8) # X_std加入一个很小的数防止分母除以0
    return X, X_mean, X_std

# 将训练集拆成训练集和验证集，默认值是0.25，可以调
def _train_dev_split(X, Y, dev_ratio=0.25):
    train_size = int(len(X) * (1 - dev_ratio))
    return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]

X_train, X_mean, X_std = _normalize(X_train, train=True)
X_test, _, _ = _normalize(X_test, train=False, specified_column=None, X_mean=X_mean, X_std=X_std)

dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio=dev_ratio)

train_size = X_train.shape[0]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]

print('Size of training set: {}'.format(train_size))
print('Size of development set: {}'.format(dev_size))
print('Size of testing set: {}'.format(test_size))
print('Dimension of data: {}'.format(data_dim))

打印结果

二.一些有用的函数

按顺序打乱X和Y，即打乱后，X[i]对应的仍是Y[i]，上面加了seed

def _shuffle(X, Y):
    randomize = np.arange(len(X))        # 建立一个0-X的列表
    np.random.shuffle(randomize)         # 生成大小为randomize的随机列表，
    return (X[randomize], Y[randomize])

sigmoid函数和逻辑回归的方程

def _sigmoid(z):
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))  
#为避免溢出，设置了最大最小值，即如果sigmoid函数的最小值比1e-8小，只会输出1e-8；而比1 - (1e-8)大，则只输出1 - (1e-8)


def _f(X, w, b):
    return _sigmoid(np.matmul(X, w) + b) # 在np.matmul(X, w)的基础上，数列中的每个值都加b得到最终的数列

将sigmoid中获得的值四舍五入转换成0或1(int型)，注意如果正好为0.5，(虽然几率很小)结果是0

def _predict(X, w, b):
    return np.round(_f(X, w, b)).astype(np.int64)

模型正确率

def _accuracy(Y_pred, Y_label):
    acc = 1 - np.mean(np.abs(Y_pred - Y_label)) # np.abs(Y_pred - Y_label) 如果预测正确，则结果是0，否则结果是1，那么我们求mean平均值的话所得值是1的概率(mean相当于 1的个数/总个数)
    return acc

三.梯度与损失

计算交叉熵，和要调整的w参数的gradient与b参数的gradient

def _cross_entropy_loss(y_pred, Y_label):
    cross_entropy = -np.dot(Y_label, np.log(y_pred)) - np.dot((1 - Y_label), np.log(1 - y_pred))
    return cross_entropy

def _gradient(X, Y_label, w, b):
    y_pred = _f(X, w, b)                                  # 预测值
    pred_error = Y_label - y_pred                         # 真实值-预测值
    w_grad = -np.sum(pred_error * X.T, 1)                 # X.T就是X的转置，axis取值为1时代表将每一行的元素相加，实际上返回的是1行510列的数组
    b_grad = -np.sum(pred_error)                          # 对b求偏微分后的结果，因为逻辑回归和线性回归的损失函数相似，可由线性回归对b进行求偏微分得到
    return w_grad, b_grad

四.模型训练

使用小批次梯度下降法来训练。训练集被分为许多小批次，针对每一个小批次，分别计算其梯度以及损失，并根据该批次来更新模型的参数。

当一次迭代完成，也就是整个训练集的所有小批次都被使用过一次以后，我们将所有训练资料打散并且重新分成新的小批次，进行下一个迭代，直到事先设定的迭代数量达成为止。

# 使用0初始化w和b参数
w = np.zeros((data_dim,))
b = np.zeros((1,))


max_iter = 10  # 迭代次数
batch_size = 8  # 训练的批次中的数据个数
learning_rate = 0.2 # 学习率


# 将每次迭代的损失和正确率都保存，以方便画出来
train_loss = []  # 训练集损失
dev_loss = []    # 验证集损失
train_acc = []   # 训练集正确率
dev_acc = []     # 验证集正确率
# 记录参数更新的次数
step = 1

# 迭代训练
for epoch in range(max_iter):
    # 随机的将训练集X和Y按顺序打乱
    X_train, Y_train = _shuffle(X_train, Y_train)

    # 小批量训练
    for idx in range(int(np.floor(train_size / batch_size))):                     # 每个批次8个数据，一共48830个数据，共48830/8=6103次批次
        X = X_train[idx * batch_size:(idx + 1) * batch_size]                      # 分别取X和Y中的对应8个数据(每个批次8个数据)
        Y = Y_train[idx * batch_size:(idx + 1) * batch_size]

        # 计算w参数和b参数的梯度
        w_grad, b_grad = _gradient(X, Y, w, b)


        # 更新参数，自适应学习率，学习率除以更新次数的根
        w = w - learning_rate / np.sqrt(step) * w_grad
        b = b - learning_rate / np.sqrt(step) * b_grad

        step = step + 1   # 更新次数+1

    # 计算训练集和验证集的损失和正确率
    y_train_pred = _f(X_train, w, b)                                              # 计算预测的值，注意此时数据格式为float
    Y_train_pred = np.round(y_train_pred)                                         # 将数据格式转换为bool类型
    train_acc.append(_accuracy(Y_train_pred, Y_train))                            # 将这一轮迭代的正确率记录下来
    train_loss.append(_cross_entropy_loss(y_train_pred, Y_train) / train_size)    # 将这一次迭代的损失记录下来

    y_dev_pred = _f(X_dev, w, b)   # 同样的方法处理验证集
    Y_dev_pred = np.round(y_dev_pred)
    dev_acc.append(_accuracy(Y_dev_pred, Y_dev))
    dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev) / dev_size)

 # 输出最后依次迭代的结果
print('Training loss: {}'.format(train_loss[-1]))
print('Development loss: {}'.format(dev_loss[-1]))
print('Training accuracy: {}'.format(train_acc[-1]))
print('Development accuracy: {}'.format(dev_acc[-1]))

 输出最后迭代的结果

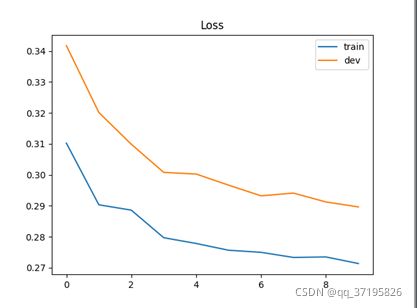
五.绘制损失和精度曲线

import matplotlib.pyplot as plt

# Loss curve
plt.plot(train_loss)
plt.plot(dev_loss)
plt.title('Loss')
plt.legend(['train', 'dev'])
plt.savefig('loss.png')
plt.show()

# Accuracy curve
plt.plot(train_acc)
plt.plot(dev_acc)
plt.title('Accuracy')
plt.legend(['train', 'dev'])
plt.savefig('acc.png')
plt.show()

loss和准确率图像 

 六.预测测试标签

预测testing data 并找出权重中最大的十项特征，即关联结果最紧密的参数。

predictions = _predict(X_test, w, b)
with open(output_fpath.format('logistic'), 'w') as f:                #预测测试集并且存在 output_logistic.csv 中。
    f.write('id,label\n')
    for i, label in  enumerate(predictions):
        f.write('{},{}\n'.format(i, label))

# 找到权重中最大的前十项，即关联结果的最紧密的参数
ind = np.argsort(np.abs(w))[::-1]                                     # 将数组从小到大排好后从最后往前取
with open(X_test_fpath) as f:
    content = f.readline().strip('\n').split(',')
features = np.array(content)
for i in ind[0:10]:
    print(features[i], w[i])

预测结果保存为csv文件

权重最大的十项

 

 

概率生成模型

一.数据准备

数据的预处理和标准化与逻辑回归一样。分别将数据中的两个类别的数据分开，这样才可以计算两个类别的数据平均值1，2

with open(X_train_fpath) as f:
    next(f)
    X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype=float)
with open(Y_train_fpath) as f:
    next(f)
    Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype=float)
with open(X_test_fpath) as f:
    next(f)
    X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype=float)

# Normalize training and testing data
X_train, X_mean, X_std = _normalize(X_train, train=True)
X_test, _, _ = _normalize(X_test, train=False, specified_column=None, X_mean=X_mean, X_std=X_std)


X_train_0 = np.array([x for x, y in zip(X_train, Y_train) if y == 0]) # 训练集中属于类别0的数据
X_train_1 = np.array([x for x, y in zip(X_train, Y_train) if y == 1]) # 训练集中属于类别0的数据

二.平均值和协方差

计算平均值和协方差，为了有效减少参数，避免Overfitting，给描述这两个类别的高斯分布相同的协方差矩阵。

mean_0 = np.mean(X_train_0, axis = 0)# 1
mean_1 = np.mean(X_train_1, axis = 0)# 1

# 计算协方差矩阵1，2
cov_0 = np.zeros((data_dim, data_dim))# 1
cov_1 = np.zeros((data_dim, data_dim))# 2
#计算
for x in X_train_0:
    cov_0 += np.dot(np.transpose([x - mean_0]), [x - mean_0]) / X_train_0.shape[0]
for x in X_train_1:
    cov_1 += np.dot(np.transpose([x - mean_1]), [x - mean_1]) / X_train_1.shape[0]

# 共享协方差矩阵计算
cov = (cov_0 * X_train_0.shape[0] + cov_1 * X_train_1.shape[0]) / (X_train_0.shape[0] + X_train_1.shape[0])

---

三.计算权重和偏差

通过奇异值分解得到共用协方差矩阵逆。有了数据平均值和协方差矩阵的逆，可以直接将唯一的权重矩阵与偏差向量计算出来。

# 通过奇异值分解得到矩阵逆。
u, s, v = np.linalg.svd(cov, full_matrices=False)
inv = np.matmul(v.T * 1 / s, u.T)                    # 计算协方差矩阵的逆

# 有了数据平均值和协方差矩阵的逆，可以直接将唯一的权重矩阵与偏差向量计算出来
w = np.dot(inv, mean_0 - mean_1)
b =  (-0.5) * np.dot(mean_0, np.dot(inv, mean_0)) + 0.5 * np.dot(mean_1, np.dot(inv, mean_1))\
    + np.log(float(X_train_0.shape[0]) / X_train_1.shape[0])                                     

四.预测测试集标签

预测并打印最重要的十个权重

# 计算训练精度
Y_train_pred = 1 - _predict(X_train, w, b)
print('Training accuracy: {}'.format(_accuracy(Y_train_pred, Y_train)))

# 预测测试集
predictions = 1 - _predict(X_test, w, b)
with open(output_fpath.format('generative'), 'w') as f:          #预测测试集并且存在 output_generative.csv 中。
    f.write('id,label\n')
    for i, label in  enumerate(predictions):
        f.write('{},{}\n'.format(i, label))

# 打印出最重要的十个权重
ind = np.argsort(np.abs(w))[::-1]
with open(X_test_fpath) as f:
    content = f.readline().strip('\n').split(',')
features = np.array(content)
for i in ind[0:10]:
    print(features[i], w[i])

总结

以上是第二个作业