0-1背包问题（动态规划，含可运行代码）

一、0-1背包问题的数学模型

1、U={u1,u2,...,un}是一个准备放入容量为C的背包中的n项物品的集合。

2、对于1≤j≤n,令wj和vj分别为第j项物品的体积和价值，这里C，wj,vj和j都是正整数。

3、要找出一个子集合SU，使得最大。

4、约束条件是：。

二、0-1背包问题求解方法

一）穷举法

     不推荐使用此法解决背包问题，算法复杂度为O()。

二）动态规划法

1、动态规划法求解思路

（1）先导出一个递归公式

         V[i,j]:从前i项{u1,u2,...,ui}中取出来的装入体积为j的背包的物品的最大价值。

         这里

（2）目标：

         V[n,C],即从n个物品中选择，装满容积为C的背包的物品的最大价值

2、背包问题解题步骤

（1）定义背包的初始化

        a. v[0,j]=0：背包中什么都没有

        b. v[i,0]=0：背包中没有任何价值的东西，即将前i项东西放入体积为0的背包中去，故也取0.

（2）当i和j都大于0时，有如下结论：

       假设V[i,j]是下面两个量的最大值。

       1）V[I-1,J]：用最优法取自{u1,u2,...,ui-1}的物品放入体积为j的背包中所得的价值的最大值。

       2）V[i-1,j-si]+vi：表示用最优方法取自{u1,u2...,ui-1}的物品去装入体积为j-wi的背包所得的最大价值加上物品ui的价值vi。

            该问题适用于对于物品ui加到背包上，以及jwi。（si是第i个物品的体积）

（3）观察结论得到如下递推式

      a)  当i=0或j=0时，V[i.j]=0；

      b) 当j＜wi时，V[i.j]=V[i-1,j];

      c) 当i＞0和j≥wi时，V[i,j]=max{V[i-1,j],V[i-1,j-wi]+vi}

3、0-1背包问题算法

INPUT：物品集合U={u1,u2,...,un},体积分别为w1,w2...,wn，价值分别为v1,v2,...,vn，容量为C的背包

OUTPUT：的最大价值，且满足≤C，其中SU

for i←0 to n

    V[i,0]←0

end for

for j←0 to C

      V[0,j]=0

end for

for i←1 to n

    for j ←1 to C

        V[i,j]←V[i-1,j]

         if si≤j and (V[i-1,j-wi]+vi)>V[i,j] then

              V[i,j]←V[i-1,j-wi]+vi

               item[j]=i

         end if

    end for

end for

for i←C down to 1 (i=i-item[i]的体积)

•       printf(item[i])

return V[n,C]

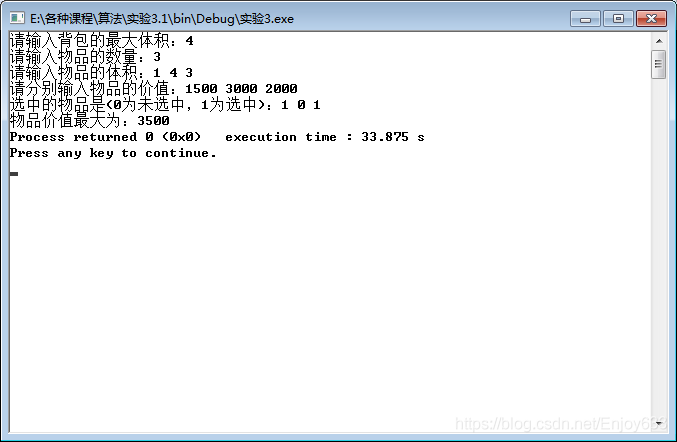
三、源代码（此代码可运行）

#include 
#include 
#include 
using namespace std;

int V[200][200];  //前i个物品装入体积为j的背包中获得的最大价值
int FindMax(int n,int w[],int v[],int x[],int C)
{
    int i,j;
    for(i=0;i<=n;i++)
    {
        V[i][0]=0;
    }
    for(j=0;j<=C;j++)
    {
        V[0][j]=0;
    }
    for(i=0;i<=n-1;i++)
    {
        for(j=0;j<=C;j++)
        {
           if(j=0;i--)
    {
        if(V[i][j]>V[i-1][j])
        {
            x[i]=1;
            j=j-w[i];
        }
        else
        {
            x[i]=0;
        }
    }
    printf("选中的物品是(0为未选中，1为选中)：");
    for(i=0;i

运行结果展示：