动态规划-经典问题（0-1背包问题）分析及优化

目录

1.0-1背包问题的分析

（1）状态方程

2.递归算法

3.记忆化搜索

4.动态规划

5.优化1——空间复杂度O(2C) 

6.优化2——空间复杂度O(C) 

7.0-1背包问题的变种

---

 如上图是一个LeetCode的经典问题，0-1背包问题

1.0-1背包问题的分析

尝试下面的算法

暴力解法：每一件物品都可以放进背包，也可以不放进背包，时间复杂度为O((2^n)*n)，需要耗费太久的时间     X

贪心算法：优先放入平均价值最高的物品，如下图例子                                                                                           X

假设有一个容量为5的背包

（1）此时如果采用贪心算法，则应该是先放入6，占了一个容量，再放入10，占了2个容量，此时一共占用了3个容量，无法继续放入第3个物品，此时贪心算法的结果就是16

（2） 但如果我们不放入1，只放入2,3物品，则此时背包容量刚好填满，价值为22。此时我们刚好放弃了平均价值最大的物品，

因此贪心算法是不正确的

（1）状态方程

F（n,C）:考虑将n个物品放进容量为C的背包，使得价值最大声

状态转移方程分析：

状态有两种，一种是该物品放进背包，一种是不放进背包，直接考虑后面的物品，两种状态取大值即可

F（i，C） = F（i-1，C）                          不放进背包，直接考虑后面的物品

                  =v（i） + F（i-1，C-w（i））该物品放进背包

状态转移方程：F（i，C）= max(F（i-1，C），v（i） + F（i-1，C-w（i））)

2.递归算法

class Solution {
    private $w,$v;  //使其成为成员变量
    public function knapsack01($w,$v,$c){
        $len = count($w);
        $this->w = $w;
        $this->v = $v;
        return $this->bestValue($len-1,$c);
    }
    /**
     * [用[0...index]的物品，填充容积为c的背包的最大价值]
     * @param  [type] $index [考虑到的物品的下标]
     * @param  [type] $c     [剩余的容量]
     */
    private function bestValue($index,$c){
        if($index < 0 || $c <= 0) return 0;
        $res = $this->bestValue($index-1,$c);       //不放入该物体，直接考虑后面的物品放入
        if($c >= $this->w[$index])                  //如果该物体能放得下该背包，则放入，并与上面的策略取大值
            $res = max($res, $this->v[$index] + $this->bestValue($index-1,$c-$this->w[$index]));
        return $res;
    }
}
$q = new Solution();
$w = [1,2,3];
$v = [6,10,12];
$c = 5;
var_dump($q->knapsack01($w,$v,$c));

3.记忆化搜索

递归解答中存在大量的重叠子结构问题，可以利用index 和 剩余容量 c 作为记忆化数组的下标

class Solution {
    private $w,$v;       //使其成为成员变量
    private $memo = [];  //初始化记忆化数组
    public function knapsack01($w,$v,$c){
        $len = count($w);
        $this->w = $w;
        $this->v = $v;
        return $this->bestValue($len-1,$c);
    }
    /**
     * [用[0...index]的物品，填充容积为c的背包的最大价值]
     * @param  [type] $index [考虑到的物品的下标]
     * @param  [type] $c     [剩余的容量]
     */
    private function bestValue($index,$c){
        if($index < 0 || $c <= 0) return 0;
        if(isset($this->memo[$index][$c]))          //检索是否已经检索过
            return $this->memo[$index][$c];
        $res = $this->bestValue($index-1,$c);       //不放入该物体，直接考虑后面的物品放入
        if($c >= $this->w[$index])                  //如果该物体能放得下该背包，则放入，并与上面的策略取大值
            $res = max($res, $this->v[$index] + $this->bestValue($index-1,$c-$this->w[$index]));
        $this->memo[$index][$c] = $res;             //保存记忆化数组
        return $res;
    }
}
$q = new Solution();
$w = [1,2,3];
$v = [6,10,12];
$c = 5;
var_dump($q->knapsack01($w,$v,$c));

4.动态规划

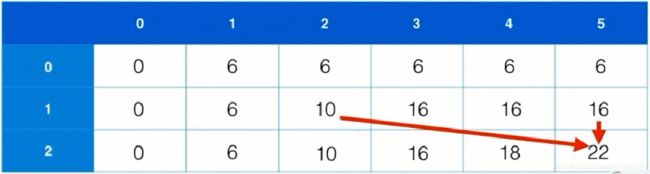
在二维数组中使用动态规划，模拟填充过程.

行为物品，列为容量

（1）填充第一行，容量为0的时候，不能填充，因此该点的价值为0。容量为1的时候，可以填充物品0，此时价值为6，往后的所有点的最大价值都为6 

 （2）填充第二行，每一个元素点都有两种可能，一种为放入该物品，另一种为不放入该物品

• 0点，无法放入物体，最大价值依旧是0；下标1，无法放入1号物品，因此最大价值为放入1号下标之前的最大收益，为6
• 下标2，可以放入物品1，因此有两种情况，不放入该物品时，所获最大价值为该容量的上一个最大收益，为6；放入该物体时，价值则等于该物体的价值10加上当前容量减去该物体所占体积的（2-2）的容量位置的最大收益的值，即为10+0 = 10 > 6,则下标2位置的最大收益变为 10
• 以此类推，一直到容量5，不放入该物体时，当前容量的最大收益为6；放入该物体时，10 + 6 = 16 > 6 ，因此该下标的最大收益为16

（3）以此类推，填充第三行，到容积为3时才能放入该物体，到最后一个下标5时，如果不放入该物体，则最大收益为上一行容量的最大收益；如果放入该物体，则最大收益为，该物体所获收益12 + 容量-该物体占用容量的容量下标所获最大收益10 10+12=22>16,因此最终答案为22

class Solution {
    public function knapsack01($w,$v,$c){
        $len = count($w);                        //求数组长度
        $dp = [];                                //初始化动态规划二维数组
        for($j = 0; $j <= $c; ++$j)              //初始化第一行数据
            $dp[0][$j] = $j >= $w[0]? $v[0]: 0;
        for($i = 1;$i < $len; ++$i){             //从第二行开始冬天规划
            for($j = 0;$j <= $c; ++$j){
                $dp[$i][$j] = $dp[$i-1][$j];     //不放入物品的策略
                if($j >= $w[$i])                 //如果物品可以放入，则取与物品可以放入的最大值
                    $dp[$i][$j] = max($dp[$i][$j], $v[$i] + $dp[$i-1][$j-$w[$i]]);
            }
        }
        return $dp[$len-1][$c];                  //最终，最后一个元素未所求答案
    }
}
$q = new Solution();
$w = [1,2,3];
$v = [6,10,12];
$c = 5;
var_dump($q->knapsack01($w,$v,$c));

5.优化1——空间复杂度O(2C) 

原本的动态规划的时间复杂度为O(n*c) ,空间复杂度为O(n*c)

状态转移方程：F（i，C）= max(F（i-1，C），v（i） + F（i-1，C-w（i））)

第i行元素只依赖于第i-1行元素，所以理论上，只需要保持两行元素即可，空间复杂度O(2*c) = O(c)

我们可以定义两行，第一行都在处理偶数的数，第二行都是奇数

通过节省空间，可以解决的问题范围就大大增加了

class Solution {
    public function knapsack01($w,$v,$c){
        $len = count($w);                         //求数组长度
        $dp = [];                                 //初始化动态规划二维数组
        for($j = 0; $j <= $c; ++$j)               //初始化第一行数据
            $dp[0][$j] = $j >= $w[0]? $v[0]: 0; 
        for($i = 1;$i < $len; ++$i){              //从第二行开始冬天规划
            for($j = 0;$j <= $c; ++$j){ 
                $dp[$i%2][$j] = $dp[($i-1)%2][$j];//不放入物品的策略
                if($j >= $w[$i])                  //如果物品可以放入，则取与物品可以放入的最大值
                    $dp[$i%2][$j] = max($dp[$i%2][$j], $v[$i] + $dp[($i-1)%2][$j-$w[$i]]);
            }
        }
        return $dp[($len-1)%2][$c];               //最终，最后一个元素未所求答案
    }
}
$q = new Solution();
$w = [1,2,3];
$v = [6,10,12];
$c = 5;
var_dump($q->knapsack01($w,$v,$c));

6.优化2——空间复杂度O(C) 

根据上面的图例，每一次更新都会参考上面和左边的内容，右边的内容不会进行操作

因此我们可以只开辟一个一维的长度为C的数组，从右往左进行动态规划

不仅可以节省时间复杂度，$j 只需遍历到比当前物体占用位置大的下标，再小就放不下去

还可以节省空间复杂度，O（C），每次都与自身（即不放入当前物体）和放入物体后取大值

简洁代码

class Solution {
    public function knapsack01($w,$v,$c){
        $len = count($w);                        //求数组长度
        $dp = [];                                //初始化动态规划二维数组
        for($j = 0; $j <= $c; ++$j)              //初始化第一行数据
            $dp[$j] = $j >= $w[0]? $v[0]: 0;
        for($i = 1;$i < $len; ++$i){             //从第二个物品开始，从右往左开始动态规划
            for($j = $c;$j >= $w[$i]; --$j){     //$j为当前的容量，当前的容量要当前物品所占用的地方，否则放不下去
                $dp[$j] = max($dp[$j], $v[$i] + $dp[$j-$w[$i]]);//跟原先的自己（即不放入该物体）和放入该物体后比较
            }
        }
        return $dp[$c];                  //最终，最后一个元素为所求答案
    }
}
$q = new Solution();
$w = [1,2,3];
$v = [6,10,12];
$c = 5;
var_dump($q->knapsack01($w,$v,$c));      //22

7.背包问题求出解

（1）先求得动态规划数组

（2）从最后一个元素倒推回去，先看最后一个节点22。22不等于上一个元素16，因此证明该位置是有经过+法的，因此2号物品是肯定有放进背包的

（3） 判断1号物品是否放进去，判断[ 0，2]。10=[0,0]位置的价值+1号物品的价值10 而不等于 [0,2]位置的6，因此证明1号物品也有放进去

（4） [0,0]位置为0，明显看出0号物品没有放进背包

（5） 要求出所有解就不能优化dp的空间为O（n），因为求出所有解需要dp包含之前所有的数据

8.0-1背包问题的变种

完全背包问题：每个物品可以无限使用

多重背包问题：每个物品不止1个，有num(i)个

多维费用背包问题：要同时考虑物品的体积和重量两个维度

物品之间互相排斥/互相依赖

……各种约束，脑瓜疼