ch6_8 优先级队列实现堆, 前K 个高频元素
引言
计算机系统中经常会遇到这样一类问题:前一个任务已经执行完成,需要在待执行任务中挑选一个新的任务执行。
最简单的方法就是将所有的任务排成一个队列,按照队列的先进先出(FIFO)的策略挑选要执行的任务。这种策略虽然保证了所有的任务都能被执行,但是往往会导致执行时间短的或者紧急度高的任务在队列中等待时间较长而导致效率低下。
另一种策略是为每个任务安排一个优先级,每次挑选任务时只需要从队列中取出优先级最高的任务执行即可。实现该策略需要借助一种特殊的数据结构:优先级队列(PriorityQueue)。
- 完全二叉树
- 满足 堆序性的 完全二叉树 形成堆,
- 使用 优先级队列 实现堆;
1. 完全二叉树
全二叉树的定义如下:
在完全二叉树中,
-
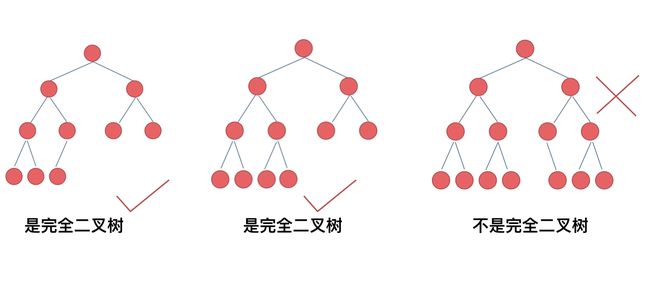
除了最底层节点可能没填满外,其余每层节点数都达到最大值,若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
-
并且最下面一层的节点都集中在该层最左边的若干位置。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
来举一个典型的例子如题:
1. 1 完全二叉树的存储
比较适合用 数组来存储,完全二叉树,
理由:因为使用数组存储时, 可以使用数组的下标, 求得某个节点的左右节点 以及对应的 父亲节点; 从而不需要存储左右子节点的指针, 从而节省存储空间;
当前节点存储在数组中的下标为 i, 则
父节点: [ i / 2] 下取整;
左右 子节点的 下标 分别为: 2i, 2i + 1;
2. 堆
满足堆的条件:
- 堆必须是一个完全二叉树; 即除了最底层, 其他层的节点都被元素填满, 且最底层的节点按照从左到右的 顺序依次填满;
- 满足堆序性; 即是大根堆 或者 小根堆;
注意, 堆总是一颗完全二叉树, 而二叉树却不一定是堆;
满足堆序性的 二叉树 才作为堆;
树中所有元素都小于它的所有后裔节点, 最小元素是根节点, 此时是 小根堆;
而如果树中所有元素都大于它的所有后裔节点, 最大元素是根节点, 此时是 大根堆;
2.1 堆的实现
既然完全二叉树 使用 数组实现, 而堆必定是完全二叉树, 那么 堆可以用数组实现;
3.优先级队列(priority Queue)
优先级队列虽然也叫队列,但是和普通的队列还是有差别的。普通队列出队顺序只取决于入队顺序,
3.1 定义
而优先级队列的出队顺序 与元素的优先级有关。
换句话说,优先级队列是一个自动排序的队列。元素自身的优先级, 如何定义元素的“优先级”可以有不同的实现, 可以根据入队时间,也可以根据其他因素来确定,因此非常灵活。
3.2 优先级队列的实现
优先级队列的内部实现有很多种,
例如有序数组、无序数组和。
但是无论哪种实现,优先级队列必须实现以下两种方法:insert和delete。
insert方法是将带优先级的元素插入优先级队列中(类似队列的enQueue方法);
delete方法是从优先级队列中取出最高优先级(或最低优先级)的元素并在队列中删除该元素(类似队列的出队)。
4. 前K 个高频元素, code_ python
leetcode 347, 前K 个高频元素
4.1 思路
-
建字典, 存储元素, 以及对应的频率次数;
先求出数组中各个元素出现的次数, 建立一个字典, 使用字典中的get() 方法, get(key, num) , 取出字典中 key 所对应的数值, 如果字典中没有指定的该key, 则对应的该key 取出的数值为 默认值 num; -
调用最小堆, 建立优先队列;
调用python 中内置的 heapq 堆, 该堆建立时,默认的是小根堆;
使用一个优先队列 实现堆;
优先级别, 按照 出现的频率次数;
注意,该优先队列存储的是多个元组,(出现的频率次数, 元素)
- 维护大小为K的小根堆, 当堆的大小超出 K, 弹出堆顶元素;
- 建立大小为K 的空数组, 倒序存放到数组中;弹出优先队列中的元组, 存储元组中的数值数值;
# 时间复杂度:O(nlogk)
# 空间复杂度:O(n)
# 1. 建字典, 存储元素,以及的频率次数;
# 2. 建立堆, 将频率的次数 存入到最小堆中;
# 3. 维护大小为 K 的最小堆; 超出 K 时, 弹出其中的堆顶元素;
# 4. 建立一个空数组, 倒序存放到空数组中;弹出优先队列中的元组,
import heapq # 导入python 内置的 堆的数据结构, 该heapp 默认构建的是 最小堆;
class Solution:
def topKFrequent(self, nums: list, k: int) -> list:
map_ = { }
for i in range(len(nums)): # 使用get 方法, 将nums[i] 作为key, nums[i]所出现的次数作为 Vaule; 获取该键对应的数值, 该键所对应的数值便是nums[i] 所出现的次数;
map_[nums[i]] = map_.get(nums[i], 0 ) + 1 # 当该键没有所对应的数值时, 返回设置的默认数值, 此处默认数值 = 0; 即 键第一次出现时, 次数加1, 后面以此出现, 继续加一;
pri_que = [] # 使用数组来存储一个优先队列, 该优先队列 使用下面的最小堆来实现;
for key, freq in map_.items(): # 使用python 内置最小堆 实现优先队列
heapq.heappush(pri_que, (freq, key)) # 建堆, 将出现的频率次数作为优先级存入到该堆中, 该堆默认的是以 最小堆存储的; 注意, 该优先队列,存放的是一个个元组; 每个元组中(freq, key)
if len(pri_que) > k:
heapq.heappop(pri_que) # 维护大小为K 的最小堆, 当堆中的数目大于K, 弹出堆顶元素;
print(pri_que)
topK = [0] * k
for i in range(k-1, -1, -1): # 存放的时候, 倒序存放,按照从后往前的顺序存放;
topK[i] = heapq.heappop(pri_que)[1] # 注意, 由于优先队列 存储的是 一个个 元组, 故弹出该元组中的第二个元素, 即数值;
return topK
if __name__ == "__main__":
obj1 = Solution()
result = obj1.topKFrequent([-7, -8, 7, 5, 7, 1, 1, 6, 0, 7, 6, 6, 5, 5, 5, 5, 5, 6], 4)
print(result)