ConvNeXt原理+代码详解（通透）

ConvNeXt
论文名称： A ConvNet for the 2020s
论文下载链接： https://arxiv.org/abs/2201.03545
源码链接： https://github.com/facebookresearch/ConvNeXt
太阳花的小绿豆的视频讲解： https://www.bilibili.com/video/BV1SS4y157fu

1、前言

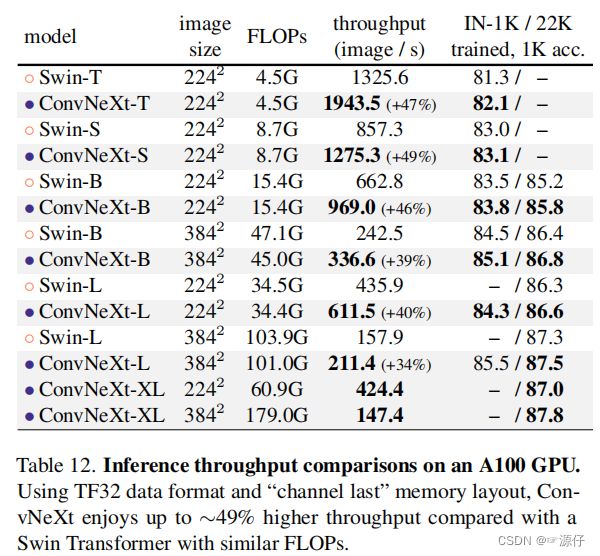
自从ViT(Vision Transformer)在CV领域大放异彩，越来越多的研究人员开始拥入Transformer的怀抱。回顾近一年，在CV领域发的文章绝大多数都是基于Transformer的，比如2021年ICCV 的best paper Swin Transformer，而卷积神经网络已经开始慢慢淡出舞台中央。卷积神经网络要被Transformer取代了吗？也许会在不久的将来。今年(2022)一月份，Facebook AI Research和UC Berkeley一起发表了一篇文章A ConvNet for the 2020s，在文章中提出了ConvNeXt纯卷积神经网络，它对标的是2021年非常火的Swin Transformer，通过一系列实验比对，在相同的FLOPs下，ConvNeXt相比Swin Transformer拥有更快的推理速度以及更高的准确率，在ImageNet 22K上ConvNeXt-XL达到了87.8%的准确率，参看下图(原文表12)。看来ConvNeXt的提出强行给卷积神经网络续了口命。

读完这篇文章你会发现ConvNeXt“毫无亮点”，ConvNeXt使用的全部都是现有的结构和方法，没有任何结构或者方法的创新。而且源码也非常的精简，100多行代码就能搭建完成，相比Swin Transformer简直不要太简单。之前看Swin Transformer时，滑动窗口，相对位置索引，不光原理理解起来有些吃力，源码多的也挺让人绝望的（但无法否认Swin Transformer的成功以及设计的很巧妙）。为什么现在基于Transformer架构的模型效果比卷积神经网络要好呢？论文中的作者认为可能是随着技术的不断发展，各种新的架构以及优化策略促使Transformer模型的效果更好，那么使用相同的策略去训练卷积神经网络也能达到相同的效果吗？抱着这个疑问作者就以Swin Transformer作为参考进行一系列实验。

In this work, we investigate the architectural distinctions between ConvNets and Transformers and try to identify the confounding variables when comparing the network performance. Our research is intended to bridge the gap between the pre-ViT and post-ViT eras for ConvNets, as well as to test the limits of what a pure ConvNet can achieve.

2、设计方案

作者首先利用训练vision Transformers的策略去训练原始的ResNet50模型，发现比原始效果要好很多，并将此结果作为后续实验的基准baseline。然后作者罗列了接下来实验包含哪些部分：

• macro design
• ResNeXt
• inverted bottleneck
• large kerner size
• various layer-wise micro designs
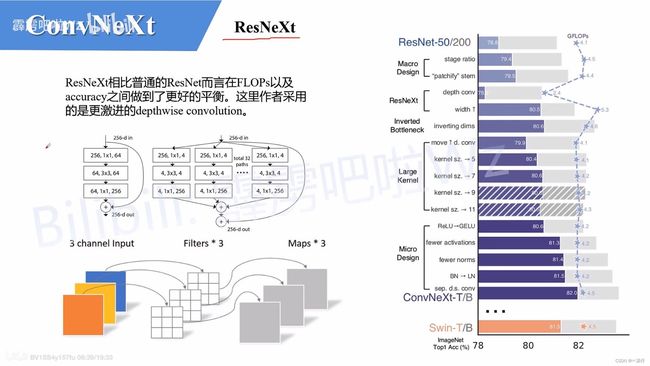
  下图（原论文图2）展现了每个方案对最终结果的影响（Imagenet 1K的准确率）。很明显最后得到的ConvNeXt在相同FLOPs下准确率已经超过了Swin Transformer。接下来，针对每一个实验进行解析。
  

3、Macro design

在这个部分作者主要研究两方面：

• Changing stage compute ratio，在原ResNet网络中，一般conv4_x（即stage3）堆叠的block的次数是最多的。如下图中的ResNet50中stage1到stage4堆叠block的次数是(3, 4, 6, 3)比例大概是1:1:2:1，但在Swin Transformer中，比如Swin-T的比例是1:1:3:1，Swin-L的比例是1:1:9:1。很明显，在Swin Transformer中，stage3堆叠block的占比更高。所以作者就将ResNet50中的堆叠次数由(3, 4, 6, 3)整成(3, 3, 9, 3)，和Swin-T拥有相似的FLOPs。进行调整后，准确率由78.8%提升到了79.4%。
  
• Changing stem to “Patchify”，在之前的卷积神经网络中，一般最初的下采样模块stem一般都是通过一个卷积核大小为7x7以及stride为2的卷积层以及一个stride为2的MaxPooling下采样共同组成，高和宽都下采样4倍。但在Transformer模型中一般都是通过一个卷积核非常大且相邻窗口之间没有重叠的（即stride等于kernel_size）卷积层进行下采样。比如在Swin Transformer中采用的是一个卷积核大小为4x4以及stride为4的卷积层构成patchify，同样是下采样4倍。所以作者将ResNet中的stem也换成了和Swin Transformer一样的patchify。替换后准确率从79.4% 提升到79.5%，并且FLOPs也降低了一点。
  

4、ResNeXt-ify

接下来作者借鉴了ResNeXt中的组卷积grouped convolution，因为ResNeXt相比普通的ResNet而言在FLOPs以及accuracy之间做到了更好的平衡。而作者采用的是更激进的depthwise convolution:即group数和通道数channel相同，详细的内容可以看MobileNet论文。这样做的另一个原因是作者认为depthwise convolution和self-attention中的加权求和操作很相似。

We note that depthwise convolution is similar to the weighted sum operation in self-attention.

接着作者将最初的通道数由64调整成96和Swin Transformer保持一致，最终准确率达到了80.5%。

5、Inverted Bottleneck

作者认为Transformer block中的MLP模块非常像MobileNetV2中的Inverted Bottleneck模块，即两头细中间粗。下图a是ResNet中采用的Bottleneck模块，b是MobileNetV2采用的Inverted Botleneck模块（图b的最后一个1x1的卷积层画错了，应该是384->96，后面如果作者发现后应该会修正过来），c是ConvNeXt采用的是Inverted Bottleneck模块。关于MLP模块细节可以阅读Vision Transformer论文，关于Inverted Bottleneck模块可以参考MobileNetv2。

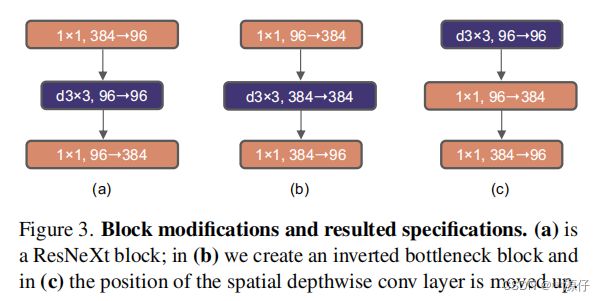
作者采用Inverted Bottleneck模块后，在较小的模型上准确率由80.5%提升到了80.6%，在较大的模型上准确率由81.9%提升到82.6%。

Interestingly, this results in slightly improved performance (80.5% to 80.6%). In the ResNet-200 / Swin-B regime, this step brings even more gain (81.9% to 82.6%) also with reduced FLOPs.

6、Large Kernel Sizes

在Transformer中一般都是对全局做self-attention，比如Vision Transformer。即使是Swin Transformer也有7x7大小的窗口。但现在主流的卷积神经网络都是采用3x3大小的窗口，因为之前VGG论文中说通过堆叠多个3x3的窗口可以替代一个更大的窗口，而且现在的GPU设备针对3x3大小的卷积核做了很多的优化，所以会更高效。接着作者做了如下两个改动：

• Moving up depthwise conv layer，即将depthwise conv模块上移，原来是1x1 conv -> depthwise conv -> 1x1 conv，现在变成了depthwise conv -> 1x1 conv -> 1x1 conv。这么做是因为在Transformer中，MSA模块是放在MLP模块之前的，所以这里进行效仿，将depthwise conv上移。这样改动后，准确率下降到了79.9%，同时FLOPs也减小了。
• Increasing the kernel size，接着作者将depthwise conv的卷积核大小由3x3改成了7x7（和Swin Transformer一样），当然作者也尝试了其他尺寸，包括3, 5, 7, 9, 11发现取到7时准确率就达到了饱和。并且准确率从79.9% (3×3) 增长到 80.6% (7×7)。
  

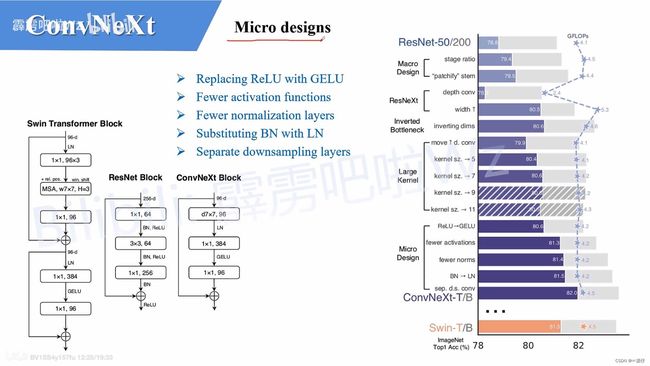
7、Micro Design

接下来作者在聚焦到一些更细小的差异，比如激活函数以及Normalization。

• Replacing ReLU with GELU，在Transformer中激活函数基本用的都是GELU，而在卷积神经网络中最常用的是ReLU，于是作者又将激活函数替换成了GELU，替换后发现准确率没变化。

• Fewer activation functions，使用更少的激活函数。在卷积神经网络中，一般会在每个卷积层或全连接后都接上一个激活函数。但在Transformer中并不是每个模块后都跟有激活函数，比如MLP中只有第一个全连接层后跟了GELU激活函数。接着作者在ConvNeXt Block中也减少激活函数的使用，如下图所示，减少后发现准确率从80.6%增长到81.3%。
  

• Fewer normalization layers，使用更少的Normalization。同样在Transformer中，Normalization使用的也比较少，接着作者也减少了ConvNeXt Block中的Normalization层，只保留了depthwise conv后的Normalization层。此时准确率已经达到了81.4%，已经超过了Swin-T。

• Substituting BN with LN，将BN替换成LN。Batch Normalization（BN）在卷积神经网络中是非常常用的操作了，它可以加速网络的收敛并减少过拟合（但用的不好也是个大坑）。但在Transformer中基本都用的Layer Normalization（LN），因为最开始Transformer是应用在NLP领域的，BN又不适用于NLP相关任务。接着作者将BN全部替换成了LN，发现准确率还有小幅提升达到了81.5%。

• Separate downsampling layers，单独的下采样层。在ResNet网络中stage2-stage4的下采样都是通过将主分支上3x3的卷积层步距设置成2，捷径分支上1x1的卷积层步距设置成2进行下采样的。但在Swin Transformer中是通过一个单独的Patch Merging实现的。接着作者就为ConvNext网络单独使用了一个下采样层，就是通过一个Laryer Normalization加上一个卷积核大小为2步距为2的卷积层构成。更改后准确率就提升到了82.0%。

8、ConvNeXt variants

对于ConvNeXt网络，作者提出了T/S/B/L四个版本，计算复杂度刚好和Swin Transformer中的T/S/B/L相似。

We construct different ConvNeXt variants, ConvNeXt-T/S/B/L, to be of similar complexities to Swin-T/S/B/L.

这四个版本的配置如下：

• ConvNeXt-T: C = (96, 192, 384, 768), B = (3, 3, 9, 3)
• ConvNeXt-S: C = (96, 192, 384, 768), B = (3, 3, 27, 3)
• ConvNeXt-B: C = (128, 256, 512, 1024), B = (3, 3, 27, 3)
• ConvNeXt-L: C = (192, 384, 768, 1536), B = (3, 3, 27, 3)
• ConvNeXt-XL: C = (256, 512, 1024, 2048), B = (3, 3, 27, 3)
  其中C代表4个stage中输入的通道数，B代表每个stage重复堆叠block的次数。

9、ConvNeXt-T 结构图

代码部分

1、Stochastic Depth

代码下载地址：pytorch_classification/ConvNeXt
论文地址：Deep Networks with Stochastic Depth
为了方便实现，这里用的并不是源码。
 DropPath/drop_path 是一种正则化手段，其效果是将深度学习模型中的多分支结构随机”删除“，python中实现如下所示：

def drop_path(x, drop_prob: float = 0., training: bool = False):
    """Drop paths (Stochastic Depth) per sample (when applied in main path of residual blocks).

    This is the same as the DropConnect impl I created for EfficientNet, etc networks, however,
    the original name is misleading as 'Drop Connect' is a different form of dropout in a separate paper...
    See discussion: https://github.com/tensorflow/tpu/issues/494#issuecomment-532968956 ... I've opted for
    changing the layer and argument names to 'drop path' rather than mix DropConnect as a layer name and use
    'survival rate' as the argument.

    """
    # 这里只返回x， return x下面的代码无用
    if drop_prob == 0. or not training:
        return x
    keep_prob = 1 - drop_prob
    shape = (x.shape[0],) + (1,) * (x.ndim - 1)  # work with diff dim tensors, not just 2D ConvNets
    random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
    random_tensor.floor_()  # binarize
    # 现实中我们是批处理的，即有batch_size个x xx，drop path的做法是：这batch_size个x xx各自独立地以p pp概率置为0。
    output = x.div(keep_prob) * random_tensor
    return output


class DropPath(nn.Module):
    """Drop paths (Stochastic Depth) per sample  (when applied in main path of residual blocks).
    """
    def __init__(self, drop_prob=None):
        super(DropPath, self).__init__()
        self.drop_prob = drop_prob

    def forward(self, x):
        return drop_path(x, self.drop_prob, self.training)

为什么要div(除以)keep_prob，即1 − p 1-p1−p。这个其实不是drop path提出的，而是dropout提出时就这么做的：

import torch
a=torch.rand(2,3,3)

import torch.nn.functional as tnf
tnf.dropout(a,p=0.5)

可以发现上面不为0的元素大小是原来的2倍。即x.div(0.5)，然后再随机失活置为0。

所以为什么drop path要这么实现归结为为什么dropout要这样实现，下面是解释：

假设一个神经元的输出激活值为a，在不使用dropout的情况下，其输出期望值为a，如果使用了dropout，神经元就可能有保留和关闭两种状态，把它看作一个离散型随机变量，它就符合概率论中的0-1分布，其输出激活值的期望变为(1-p)a+p0= (1-p)a，此时若要保持期望和不使用dropout时一致，就要除以 (1-p)。

上述代码拆分讲解：

import torch

drop_prob = 0.2
keep_prob = 1 - drop_prob
x = torch.randn(4, 3, 2, 2)
shape = (x.shape[0],) + (1,) * (x.ndim - 1)
random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
random_tensor.floor_()
output = x.div(keep_prob) * random_tensor

OUT:

x.size():[4,3,2,2]
x：
tensor([[[[ 1.3833, -0.3703],
          [-0.4608,  0.6955]],
         [[ 0.8306,  0.6882],
          [ 2.2375,  1.6158]],
         [[-0.7108,  1.0498],
          [ 0.6783,  1.5673]]],

        [[[-0.0258, -1.7539],
          [-2.0789, -0.9648]],
         [[ 0.8598,  0.9351],
          [-0.3405,  0.0070]],
         [[ 0.3069, -1.5878],
          [-1.1333, -0.5932]]],

        [[[ 1.0379,  0.6277],
          [ 0.0153, -0.4764]],
         [[ 1.0115, -0.0271],
          [ 1.6610, -0.2410]],
         [[ 0.0681, -2.0821],
          [ 0.6137,  0.1157]]],

        [[[ 0.5350, -2.8424],
          [ 0.6648, -1.6652]],
         [[ 0.0122,  0.3389],
          [-1.1071, -0.6179]],
         [[-0.1843, -1.3026],
          [-0.3247,  0.3710]]]])

random_tensor.size():[4, 1, 1, 1]
random_tensor：
tensor([[[[0.]]],
        [[[1.]]],
        [[[1.]]],
        [[[1.]]]])

output.size():[4,3,2,2]
output：
tensor([[[[ 0.0000, -0.0000],
          [-0.0000,  0.0000]],
         [[ 0.0000,  0.0000],
          [ 0.0000,  0.0000]],
         [[-0.0000,  0.0000],
          [ 0.0000,  0.0000]]],

        [[[-0.0322, -2.1924],
          [-2.5986, -1.2060]],
         [[ 1.0748,  1.1689],
          [-0.4256,  0.0088]],
         [[ 0.3836, -1.9848],
          [-1.4166, -0.7415]]],

        [[[ 1.2974,  0.7846],
          [ 0.0192, -0.5955]],
         [[ 1.2644, -0.0339],
          [ 2.0762, -0.3012]],
         [[ 0.0851, -2.6027],
          [ 0.7671,  0.1446]]],

        [[[ 0.6687, -3.5530],
          [ 0.8310, -2.0815]],
         [[ 0.0152,  0.4236],
          [-1.3839, -0.7723]],
         [[-0.2303, -1.6282],
          [-0.4059,  0.4638]]]])

random_tensor作为是否保留分支的直接置0项，若drop_path的概率设为0.2，random_tensor中的数有0.2的概率为0，而output中被保留概率为0.8。

结合drop_path的调用，若x为输入的张量，其通道为[B,C,H,W]，那么drop_path的含义为在一个Batch_size中，随机有drop_prob的样本(指)，不经过主干，而直接由分支进行恒等映射。

以上参考以下两篇博客（在此真心的感谢两位博主）：

• （以pytorch为例）路径（深度）的正则化方法的简单理解-drop path
• 【正则化】DropPath/drop_path用法

2、 Block

class Block(nn.Module):
    r""" ConvNeXt Block. There are two equivalent implementations:
    (1) DwConv -> LayerNorm (channels_first) -> 1x1 Conv -> GELU -> 1x1 Conv; all in (N, C, H, W)
    (2) DwConv -> Permute to (N, H, W, C); LayerNorm (channels_last) -> Linear -> GELU -> Linear; Permute back
    We use (2) as we find it slightly faster in PyTorch

    Args:
        dim (int): Number of input channels.
        drop_rate (float): Stochastic depth rate. Default: 0.0
        layer_scale_init_value (float): Init value for Layer Scale. Default: 1e-6.
    """
    def __init__(self, dim, drop_rate=0., layer_scale_init_value=1e-6):
        super().__init__()
        self.dwconv = nn.Conv2d(dim, dim, kernel_size=7, padding=3, groups=dim)  # 这里使用的是depthwise conv，group=channal数
        self.norm = LayerNorm(dim, eps=1e-6, data_format="channels_last")
        self.pwconv1 = nn.Linear(dim, 4 * dim)  # pointwise/1x1 convs, implemented with linear layers 
        self.act = nn.GELU()
        self.pwconv2 = nn.Linear(4 * dim, dim)  # 1乘1卷积等于全连接，作用是一样的
        # self.gamma:就是layer scale
        self.gamma = nn.Parameter(layer_scale_init_value * torch.ones((dim,)),
                                  requires_grad=True) if layer_scale_init_value > 0 else None
        self.drop_path = DropPath(drop_rate) if drop_rate > 0. else nn.Identity()

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        shortcut = x
        x = self.dwconv(x)
        x = x.permute(0, 2, 3, 1)  # [N, C, H, W] -> [N, H, W, C]
        x = self.norm(x)
        x = self.pwconv1(x)
        x = self.act(x)
        x = self.pwconv2(x)
        if self.gamma is not None:
            x = self.gamma * x
        x = x.permute(0, 3, 1, 2)  # [N, H, W, C] -> [N, C, H, W]

        x = shortcut + self.drop_path(x)
        return x

3、 ConvNeXt

class ConvNeXt(nn.Module):
    r""" ConvNeXt
        A PyTorch impl of : `A ConvNet for the 2020s`  -
          https://arxiv.org/pdf/2201.03545.pdf
    Args:
        in_chans (int): Number of input image channels. Default: 3
        num_classes (int): Number of classes for classification head. Default: 1000
        depths (tuple(int)): Number of blocks at each stage. Default: [3, 3, 9, 3]
        dims (int): Feature dimension at each stage. Default: [96, 192, 384, 768]
        drop_path_rate (float): Stochastic depth rate. Default: 0.
        layer_scale_init_value (float): Init value for Layer Scale. Default: 1e-6.
        head_init_scale (float): Init scaling value for classifier weights and biases. Default: 1.
    """
    def __init__(self, in_chans: int = 3, num_classes: int = 1000, depths: list = None,
                 dims: list = None, drop_path_rate: float = 0., layer_scale_init_value: float = 1e-6,
                 head_init_scale: float = 1.):
        super().__init__()
        self.downsample_layers = nn.ModuleList()  # stem and 3 intermediate downsampling conv layers
        # stem :kernel  4,stride = 4
        stem = nn.Sequential(nn.Conv2d(in_chans, dims[0], kernel_size=4, stride=4),
                             LayerNorm(dims[0], eps=1e-6, data_format="channels_first"))
        self.downsample_layers.append(stem)

        # 对应stage2-stage4前的3个downsample(4个block之间连接的三个下采样)
        for i in range(3):
            downsample_layer = nn.Sequential(LayerNorm(dims[i], eps=1e-6, data_format="channels_first"),
                                             nn.Conv2d(dims[i], dims[i+1], kernel_size=2, stride=2))
            self.downsample_layers.append(downsample_layer)
		# self.downsample_layers中就包含了stem和三个下采样
		
        self.stages = nn.ModuleList()  # 4 feature resolution stages, each consisting of multiple blocks
        dp_rates = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))]
        cur = 0
        # 构建每个stage中堆叠的block
        for i in range(4):
        	# 每个block乘以对应的depths=[3,3,9,3]
            stage = nn.Sequential(
                *[Block(dim=dims[i], drop_rate=dp_rates[cur + j], layer_scale_init_value=layer_scale_init_value)
                  for j in range(depths[i])]
            )
            self.stages.append(stage)
            cur += depths[i]

        self.norm = nn.LayerNorm(dims[-1], eps=1e-6)  # final norm layer
        self.head = nn.Linear(dims[-1], num_classes)
        self.apply(self._init_weights)
        self.head.weight.data.mul_(head_init_scale)
        self.head.bias.data.mul_(head_init_scale)

    def _init_weights(self, m):
        if isinstance(m, (nn.Conv2d, nn.Linear)):
            nn.init.trunc_normal_(m.weight, std=0.2)
            nn.init.constant_(m.bias, 0)

    def forward_features(self, x: torch.Tensor) -> torch.Tensor:
        for i in range(4):
            x = self.downsample_layers[i](x)
            x = self.stages[i](x)

        # global average pooling, (N, C, H, W) -> (N, C)
        return self.norm(x.mean([-2, -1]))  # x.mean([-2, -1])就是对H和W求均值，相当于平均池化


    def forward(self, x: torch.Tensor) -> torch.Tensor:
        x = self.forward_features(x)
        x = self.head(x)
        return x