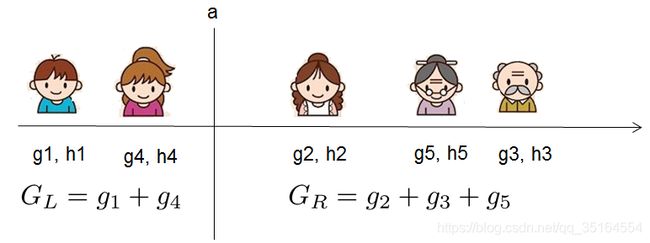一文读懂XGBoost|机器学习
XGBoost
和GBDT一样,XGBoost也是一种基于CART树的Boosting算法,让我们来看一下如何通俗的去理解XGBoost。
先简单的回想一下,在我们之前提到过的GBDT中是怎样用很多棵树去做预测的?很简单,我们给了每棵树不同的训练数据,得到多种不同的结果,最终我们把这些结果相加作为最终的预测值就可以了。
XGBoost的定义
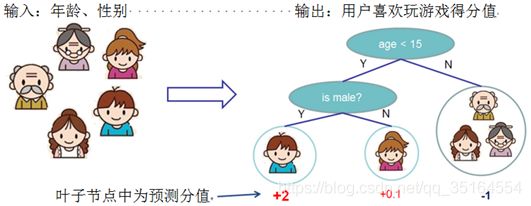
举一个简单的例子,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,最终给每个人在电子游戏上的喜爱程度进行打分,如下图所示:
我们把上图中得到的树记为tree1,同样我们可以根据日常是否使用电脑来进行新一次的打分,如下图所示:
这样我们就训练好的两棵树tree1和tree2,我们把两棵树的评分结果相加就是最终的结果,如上图中,男孩的得分是2+0.9=2.9,爷爷的得分是-1-0.9=-1.9。
看完了这个例子,你可能会疑惑,这个过程和GBDT不是一样的吗?其实在本质上XGBoost和GBDT的差异就在于目标函数的定义上,别急,继续往下看。
XGBoost的目标函数
看懂了上节中的例子,不难说出XGBoost的核心就是不断的添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数,去拟合上次预测的残差。用数学来表示这个模型,如下所示:
y ^ i = ∑ k = 1 K f k ( x i ) , f k ∈ F \hat{y}_i=\sum_{k=1}^Kf_k(x_i),f_k\in F y^i=k=1∑Kfk(xi),fk∈F
这里的K就是树的棵树,F表示所有可能的CART树,f表示一颗具体的CART树,这个模型由K棵CART树组成。有了模型之后,我们的问题也就来了,模型的参数是什么?优化参数的目标函数是什么?
先不考虑参数的问题,我们先来明确一下我们的目标。
显然,我们的目标是要使得树群的预测值 y ^ i \hat{y}_i y^i尽量接近真实值 y i y_i yi,而且要有尽量大的泛化能力。
所以从数学的角度看,目标就变成了一个泛函数的最优化问题,我们把目标函数简化成如下的形式:
o b j ( θ ) = ∑ i = 1 n l ( y i , y i ^ ) + ∑ k = 1 K Ω ( f k ) obj(\theta)=\sum_{i=1}^nl(y_i,\hat{y_i})+\sum_{k=1}^K\Omega(f_k) obj(θ)=i=1∑nl(yi,yi^)+k=1∑KΩ(fk)
这个目标函数分为两部分:损失函数和正则化项。且损失函数揭示训练误差(即预测分数和真实分数的差距),这里的正则化项由K棵树的正则化项相加而来,也可以说**正则化定义复杂度。**损失函数我们都接触过,树的正则化又是怎样的形式呢,我们后面再做说明。
XGBoost的训练
上节中我们得到了XGBoost的损失函数是加法的形式,我们不妨使用加法训练的方式分步骤对目标函数进行优化,首先优化第一棵树,接下来是第二棵…直至K棵树全被优化完成。优化的过程如下所示:
y ^ i ( 0 ) = 0 \hat{y}_i^{(0)}=0 y^i(0)=0
y ^ i ( 1 ) = f 1 ( x i ) = y ^ i ( 0 ) + f 1 ( x i ) \hat{y}_i^{(1)}=f_1(x_i)=\hat{y}_i^{(0)}+f_1(x_i) y^i(1)=f1(xi)=y^i(0)+f1(xi)
y ^ i ( 2 ) = f 1 ( x i ) + f 2 ( x i ) = y ^ i ( 1 ) + f 2 ( x i ) \hat{y}_i^{(2)}=f_1(x_i)+f_2(x_i)=\hat{y}_i^{(1)}+f_2(x_i) y^i(2)=f1(xi)+f2(xi)=y^i(1)+f2(xi)
…
y ^ i ( k ) = ∑ k = 1 t f k ( x i ) = y ^ i ( t − 1 ) + f t ( x i ) \hat{y}_i^{(k)}=\sum_{k=1}^tf_k(x_i)=\hat{y}_i^{(t-1)}+f_t(x_i) y^i(k)=∑k=1tfk(xi)=y^i(t−1)+ft(xi)
在第t次迭代的时候,我们添加了一棵最优的CART树 f t f_t ft,那么这棵树是怎么得到的呢?其实就是在现有的t-1棵树的基础上,使得目标函数最小的那棵CART树,如下所示:
o b j ( t ) = ∑ i = 1 n l ( y i , y ^ i ( t ) ) + ∑ i = 1 t Ω ( f i ) obj^{(t)}=\sum_{i=1}^nl(y_i,\hat{y}_i^{(t)})+\sum_{i=1}^t\Omega(f_i) obj(t)=∑i=1nl(yi,y^i(t))+∑i=1tΩ(fi)
= ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t \space\space\space\space\space\space\space\space\space=\sum_{i=1}^nl(y_i,\hat{y}_i^{(t-1)}+f_t{(x_i)})+\Omega(f_t)+constant =∑i=1nl(yi,y^i(t−1)+ft(xi))+Ω(ft)+constant
根据化简后的式子,我们知道里面的损失函数,也知道里面的正则项,那么constant又是哪来的呢?(这里是不是有很多问号),先别急,马上就会揭晓答案。
说到这,我们一直都是用抽象的方式去表示损失函数,我们可以考虑当损失函数是均方误差(MSE)的情况(也就是: l ( y i , y ^ i ) = ( y i − y ^ i ) 2 l(y_i,\hat{y}_i)=(y_i-\hat{y}_i)^2 l(yi,y^i)=(yi−y^i)2),此时我们的目标函数可以改写成如下的形式:
o b j ( t ) = ∑ i = 1 n ( y i − ( y ^ i ( t − 1 ) + f t ( x i ) ) ) 2 + Ω ( f t ) + c o n s t a n t obj^{(t)}=\sum_{i=1}^n(y_i-(\hat{y}_i^{(t-1)}+f_t(x_i)))^2+\Omega(f_t)+constant obj(t)=∑i=1n(yi−(y^i(t−1)+ft(xi)))2+Ω(ft)+constant
= ∑ i = 1 n [ 2 ( y ^ i ( t − 1 ) − y i ) f t ( x i ) + f t ( x i ) 2 ] + Ω ( f t ) + c o n s t a n t \space\space\space\space\space\space\space\space\space=\sum_{i=1}^n[2(\hat{y}_i^{(t-1)}-y_i)f_t(x_i)+f_t(x_i)^2]+\Omega(f_t)+constant =∑i=1n[2(y^i(t−1)−yi)ft(xi)+ft(xi)2]+Ω(ft)+constant
替换成MSE后,又有新的问题出现了,我们是如何得到上面的式子的呢?其实,在这里我们利用了泰勒二阶展开去做了目标函数的近似(XGBoost的核心所在),我们来看一下进行泰勒二阶展开的过程。
我们的目标函数如下:
o b j ( t ) = = ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t obj^{(t)}==\sum_{i=1}^nl(y_i,\hat{y}_i^{(t-1)}+f_t{(x_i)})+\Omega(f_t)+constant obj(t)==∑i=1nl(yi,y^i(t−1)+ft(xi))+Ω(ft)+constant
首先我们给出泰勒二阶展开的近似式:
f ( x + Δ x ) ≃ f ( x ) + f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) Δ x 2 f(x+\Delta x)\simeq f(x)+f'(x)\Delta x+\frac{1}{2}f''(x)\Delta x^2 f(x+Δx)≃f(x)+f′(x)Δx+21f′′(x)Δx2
由于目标函数中的 y i y_i yi是真实值,而且通常真实值都是已知的,所以我们不去考虑,对其他的项我们来看一下目标函数和泰勒二阶展开式的对应关系:
-
泰勒二阶展开中f里的x对应目标函数的 y ^ i ( t − 1 ) \hat{y}_i^{(t-1)} y^i(t−1)
-
泰勒二阶展开中f里的 Δ x \Delta x Δx对应目标函数里的 f t ( x i ) f_t(x_i) ft(xi)
得到目标函数的近似式:
o b j ( t ) ≃ ∑ i = 1 n [ l ( y i , y ^ i ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) + c o n s t a n t obj^{(t)}\simeq\sum_{i=1}^n[l(y_i,\hat{y}_i^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+\Omega(f_t)+constant obj(t)≃∑i=1n[l(yi,y^i(t−1))+gift(xi)+21hift2(xi)]+Ω(ft)+constant
其中:gi和hi的表示如下:
g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ i ( t − 1 ) ) g_i=\partial_{\hat{y}^{(t-1)}}l(y_i,\hat{y}_i^{(t-1)}) gi=∂y^(t−1)l(yi,y^i(t−1))
h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ i ( t − 1 ) ) h_i=\partial_{\hat{y}^{(t-1)}}^2l(y_i,\hat{y}_i^{(t-1)}) hi=∂y^(t−1)2l(yi,y^i(t−1))
如果是MSE则结果如下:
g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ i ( t − 1 ) ) = 2 ( y ^ i ( t − 1 ) − y i ) g_i=\partial_{\hat{y}^{(t-1)}}l(y_i,\hat{y}_i^{(t-1)})=2(\hat{y}_i^{(t-1)}-y_i) gi=∂y^(t−1)l(yi,y^i(t−1))=2(y^i(t−1)−yi)
h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ i ( t − 1 ) ) = 2 h_i=\partial_{\hat{y}^{(t-1)}}^2l(y_i,\hat{y}_i^{(t-1)})=2 hi=∂y^(t−1)2l(yi,y^i(t−1))=2
这也就解释了我们在将MSE作为损失函数的时候,为什么会得到一个奇怪的目标函数。同样这个过程也能够让我们对不同损失函数下的目标函数进行一个近似化简。
接下来,考虑到我们第t棵回归树是根据前面的t-1棵回归树的残差得来的,相当于t-1颗树的预测值 y ^ i ( t − 1 ) \hat{y}_i^{(t-1)} y^i(t−1)是已知的,也就是说, l ( y i , y ^ i ( t − 1 ) ) l(y_i,\hat{y}_i^{(t-1)}) l(yi,y^i(t−1))对目标函数的优化不影响,我们可以直接去掉,同样常数项也可以直接移除,从而得到比较统一的目标函数:
o b j ( t ) = ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) obj^{(t)}=\sum_{i=1}^n[g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+\Omega(f_t) obj(t)=∑i=1n[gift(xi)+21hift2(xi)]+Ω(ft)
g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ i ( t − 1 ) ) g_i=\partial_{\hat{y}^{(t-1)}}l(y_i,\hat{y}_i^{(t-1)}) gi=∂y^(t−1)l(yi,y^i(t−1))
h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ i ( t − 1 ) ) h_i=\partial_{\hat{y}^{(t-1)}}^2l(y_i,\hat{y}_i^{(t-1)}) hi=∂y^(t−1)2l(yi,y^i(t−1))
到这里我们的目标函数就确定了,但是还有最后的一个小东西我们还没有介绍,下面再让我们来说一下正则项。
XGBoost的正则项
这里我们所说的正则项,也可以看作是树的复杂度。
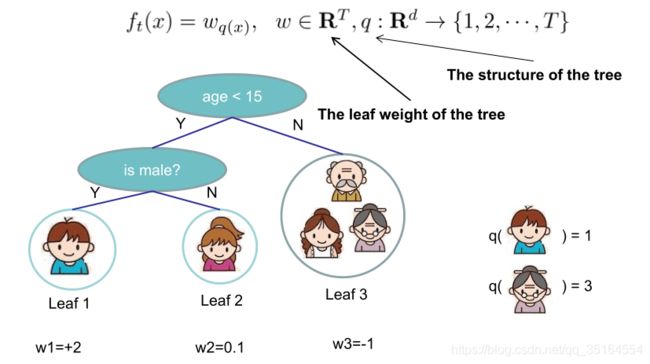
我们先对CART做一个新的定义,式子及结构表示如下:
对于图中的式子的解释:一棵树有T个叶子结点,这T个叶子节点的值组成了一个T维向量w,q(x)是一个映射,用来将样本映射成1到T的某个值,也就是把它分到某个叶子节点,q(x)其实就代表了CART树的结构。 w q ( x ) w_{q(x)} wq(x)自然就是这棵树对样本x的预测值了(得分)。
根据上面的定义,我们可以设定XGBoost的正则项包含两个部分:
- 一个是树里面叶子节点的个数T
- 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
最终表示成下图所示的形式:

这里出现了两个参数 γ \gamma γ和 λ \lambda λ,我们可以设定他们的值去调节树的结构,显然 γ \gamma γ越大,表示越希望获得结构简单的树,因为此时对较多叶子节点的树的惩罚越大, λ \lambda λ越大也是希望获得结构越简单的树。
XGBoost的最终形态
我们得到了目标函数,又得到了正则化的表达形式,不妨把他们组合在一起得到最终的结果表达:
o b j ( t ) = ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) obj^{(t)}=\sum_{i=1}^n[g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+\Omega(f_t) obj(t)=∑i=1n[gift(xi)+21hift2(xi)]+Ω(ft)
o b j ( t ) = ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + λ 1 2 ∑ j = 1 T w j 2 obj^{(t)}=\sum_{i=1}^n[g_iw_{q(x_i)}+\frac{1}{2}h_iw_{q(x_i)}^2]+\gamma T+\lambda\frac{1}{2}\sum_{j=1}^{T}w_j^2 obj(t)=∑i=1n[giwq(xi)+21hiwq(xi)2]+γT+λ21∑j=1Twj2
o b j ( t ) = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T obj^{(t)}=\sum_{j=1}^T[(\sum_{i\in I_j}g_i)w_j+\frac{1}{2}(\sum_{i\in I_j}h_i+\lambda)w_j^2]+\gamma T obj(t)=∑j=1T[(∑i∈Ijgi)wj+21(∑i∈Ijhi+λ)wj2]+γT
上式子中的 I j I_j Ij它代表一个集合 I j = { i ∣ q ( x i ) = j } I_j=\{i|q(x_i)=j\} Ij={i∣q(xi)=j},集合中每个值代表一个训练样本的序号,整个集合就是被第t棵CART树分到了第j个叶子节点上的训练样本(这个定义里的q(xi)要表达的是:每个样本值xi 都能通过函数q(xi)映射到树上的某个叶子节点,从而通过这个定义把两种累加统一到了一起)。叶子结点的个数计做T,叶子结点的分数计做W。
这样加了正则项的目标函数里就出现了两种累加:
- i->n:样本数
- j->T:叶子结点数
进一步我们可以接着对式子进行简化,定义:
G j = ∑ i ∈ I j g i G_j=\sum_{i\in I_j}g_i Gj=∑i∈Ijgi
H j = ∑ i ∈ I j h i H_j=\sum_{i\in I_j}h_i Hj=∑i∈Ijhi
简化后的式子如下:
o b j ( t ) = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T obj^{(t)}=\sum_{j=1}^T[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2]+\gamma T obj(t)=∑j=1T[Gjwj+21(Hj+λ)wj2]+γT
通过对 w j w_j wj求导等于0,可以得到:
w j ∗ = − G j H j + λ w_j^*=-\frac{G_j}{H_j+\lambda} wj∗=−Hj+λGj
然后把最优解带入得到:
o b j ∗ = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda}+\gamma T obj∗=−21∑j=1THj+λGj2+γT
这里要说明一下我们最终求得的obj表示的是这棵树的结构的好坏,值越小也就意味着结构越好,也可以说,它是衡量第t棵CART树的结构好坏的标准。但是需要注意的是,这里的好坏是与叶子结点的值没有关系的,不妨可以看一下我们的推导过程,最终的obj值与 G j , H j , T G_j,H_j,T Gj,Hj,T有关,这三者呢又只与结构q(x)有关,所以便可以得出结论就是:与叶子结点的值无关。
打分方式
拓展:我们再来换个角度理解一下 w j ∗ w_j^* wj∗
假设我们分到j这个叶子结点上的样本只有一个,则有如下的形式:
w j ∗ = ( 1 h j + λ ) ( − g j ) w_j^*=(\frac{1}{h_j+\lambda})(-g_j) wj∗=(hj+λ1)(−gj)
此时第一个括号中表示的内容可以看作是学习率,第二个括号中表示的内容可以看作是反向梯度。
XGBoost的最优树结构
有了评判树的结构好坏的标准,我们就可以先求最佳的树结构,这个定出来后,最佳的叶子结点的值实际上在上面已经求出来了。
对于我们最开始的是否喜欢电子游戏的例子,最简单的树结构就是一个结点的树,我们可以计算出这棵单结点树的好坏 o b j ∗ obj^* obj∗,假设我们现在想按照年龄将这棵单节点树进行分叉,我们需要知道:
1、按照年龄分是否有效,也就是是否减少了obj的值;
2、如果可分,那么以哪个年龄值来分。
我们按照年龄进行排序,找出所有的切分点,对于每一个切分点我们去衡量切分的好坏。示例图和计算方式如下表示:

这个Gain实际上就是单节点的 o b j ∗ obj^* obj∗减去切分后的两个节点的树 o b j ∗ obj^* obj∗,Gain如果是正的,并且值越大,表示切分后 o b j ∗ obj^* obj∗越小于单节点的 o b j ∗ obj^* obj∗,就越值得切分。同时,我们还可以观察到,Gain的左半部分如果小于右侧的 γ \gamma γ,则Gain就是负的,表明切分后 o b j ∗ obj^* obj∗反而变大了。 γ \gamma γ在这里实际上是一个临界值,它的值越大,表示我们对切分后 o b j ∗ obj^* obj∗下降幅度要求越严。这个值也是可以在XGBoost中设定的。
扫描结束后,我们就可以确定是否切分,如果切分,对切分出来的两个节点,递归地调用这个切分过程,我们就能获得一个相对较好的树结构。
注意: xgboost的切分操作和普通的决策树切分过程是不一样的。普通的决策树在切分的时候并不考虑树的复杂度,而依赖后续的剪枝操作来控制。xgboost在切分的时候就已经考虑了树的复杂度,就是那个γ参数。所以,它不需要进行单独的剪枝操作。
问题小结
至此,我们的XGBoost的原理就全都说通了,下面再来看几个通常会遇到的问题:
- obj中的constant是怎么来的?
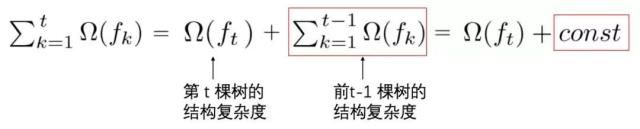
文中我们还留了一个问题没有解决,那就是constant具体是怎么来的,让我们来看一下复杂度(正则项)的迭代过程:
这样就很清晰的可以看出所谓的常数,其实就是我们前t-1棵树的复杂度加和。
- XGBoost为什么用泰勒展开?
XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了xgboost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。简单的说:使用二阶泰勒展开是为了xgboost能够自定义loss function。
- XGBoost如何寻找最优特征?是有放回还是无放回的呢?
XGBoost在训练的过程中给出各个特征的评分,从而表明每个特征对模型训练的重要性。
XGBoost利用梯度优化模型算法, 样本是不放回的,想象一个样本连续重复抽出,梯度来回踏步,这显然不利于收敛。