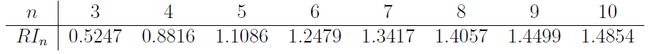python层次分析
前言 (Preface)
Through the course of a lifetime, a human makes a number of decisions, ranging from the most trivial ones that have almost no impact, to those that have life changing consequences. And almost always, these situations involve X number of options and Y number of criteria that they are judged on.
一生中,人类会做出许多决定,从几乎没有影响的最琐碎的决定,到会改变生活的后果的决定。 几乎总是这些情况涉及要对其进行判断的X个选项和Y个条件。
source 资源例子A (Example A)
Imagine you are out at the supermarket and you want to buy breakfast cereals. You are standing in front of rows and rows of cereals and not sure which one to buy. So what are you looking for?
想象一下,您在超市里,想要购买谷物早餐。 您正站在一排排的谷物前,不确定要买哪一种。 你在找什么?
Price: The cereal must not be too pricey
价格 :谷物一定不能太贵
Flavor: Maybe something with chocolate in it?
味道 :也许里面有巧克力?
Nutrition: Something with mixed fruits or oats.
营养 :混合水果或燕麦的食物。
These are some of the criteria you think of when you browse through the products. Let’s say you pick up Fruit Loops, Frosted Flakes and Lucky Charm. You mentally run each of them through the criteria and compare them against each other. Then you make a decision and put Frosted Flakes in your cart.
这些是您浏览产品时想到的一些标准。 假设您选择了水果圈,磨砂片和幸运符。 您会在心智上通过标准运行它们,并将它们相互比较。 然后,您做出决定,并将磨砂片放入购物车中。
例子B (Example B)
You are running a meeting at a town hall in a little village in Ghana. As the head of The Water Project delegation, you have been tasked to install a series of water pumps in the village. In front of you are the various stakeholders — village elders, geologists and engineers.
您正在加纳一个小村庄的市政厅举行会议。 作为水务项目代表团团长,您受命在村庄安装一系列水泵。 在您面前是各个利益相关者-乡村长者,地质学家和工程师。
In this meeting you would like to select spots for setting up the water pumps and you list out a set of criteria —
在本次会议中,您想选择安装水泵的地点,并列出一组标准-
Groundwater level: The spot must have a groundwater level that is reasonably high;
地下水位: 该地点的地下水位必须相当高;
Population: There must be a minimum number of people living nearby to make the installation useful;
人口 :为了使安装有用,附近应该居住的人数最少。
Cost: The cost of running materials and supplies must be within the project funds.
成本 :运行材料和物料的成本必须在项目资金之内。
You talk to the village elders, geologists and engineers and draw up a set of 15 possible locations to build the water pumps. After much discussion and weighing of opinions, you narrow it down to 5 spots that rank high in the list of selection criteria.
您与村庄的长者,地质学家和工程师交谈,并绘制了15个可能的位置来建造水泵。 经过大量讨论和权衡意见,您可以将其缩小到选择标准列表中排名靠前的5个位置。
Although these two examples were vastly different in their scale of impact and domain of application, the problem was pretty much the same — Making a decision in the face of multiple, often conflicting, criteria.
尽管这两个示例在影响范围和应用范围上截然不同,但问题几乎相同-面对多个(通常是相互冲突的)标准进行决策。
In this post, I will provide a high level explanation of Analytical Hierarchy Process — one possible technique of solving such multi-criteria decision making problems. And in the process, I will also show you how to implement this technique, from scratch, in Python.
在本文中,我将对层次分析过程进行高级解释,这是解决此类多准则决策问题的一种可能技术。 在此过程中,我还将向您展示如何从头开始在Python中实现这项技术。
介绍 (Introduction)
Analytical Hierarchy Process is a multi-criteria decision making method introduced by Prof. Thomas Saaty in the 1970s.
层次分析法是由Thomas Saaty教授在1970年代提出的一种多准则决策方法。
It is a way to help decision makers make informed decisions by quantifying subjective beliefs within a mathematical framework.
它是通过在数学框架内量化主观信念来帮助决策者做出明智决策的一种方法。
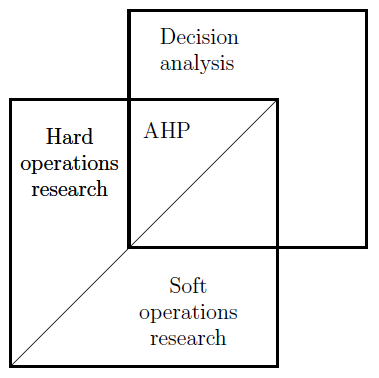
AHP is all about relative measurements of different quantities and is at the intersection of the field of decision analysis and operational research.
AHP涉及不同数量的相对测量,并且处于决策分析和运筹学领域的交汇处。
Fig. 1 —Brunelli 2015 [1] 图1 – Brunelli 2015 [1]AHP is popular in a number of fields, ranging from supply chain, to sustainable systems, environmental management, portfolio selection etc. Its popularity stems from the fact that it is highly intuitive and allows the decision maker(s) to codify their subjective beliefs in a transparent manner.
层次分析法在供应链,可持续系统,环境管理,产品组合选择等许多领域都非常受欢迎。它的广泛存在源于其高度直观的事实,并使决策者能够将其主观信念整理成事实。透明的方式。
过程 (The process)
AHP, essentially, is the process of assigning different weights to different options and summing them up. However, the beauty is in the way these weights are arrived at and therein lies the quantification of subjective beliefs.
从本质上讲,层次分析法是为不同的选项分配不同的权重并进行汇总的过程。 然而,美丽在于达到这些权重的方式,而这正是主观信念的量化。
Let me briefly present to you the highly intuitive process of AHP —
让我向您简要介绍AHP的高度直观的过程-
Step 1: Define the ultimate goal of the process. In the examples shared above, the goals were buying a breakfast cereal and selecting suitable installation spots respectively;
步骤1:定义流程的最终目标。 在上面共享的示例中,目标是分别购买早餐谷物和选择合适的安装地点;
Step 2: List the various options you have in hand to fulfill the goal. These options are called ‘alternatives’.
第2步:列出实现目标所需的各种选择。 这些选项称为“替代” 。
Step 3: List out the different criteria by which you assess the above alternatives. These can involve sub-levels of criteria and is totally dependent on the amount of scrutiny you want, especially when the options are very similar to each other.
步骤3 :列出评估上述替代方案的不同标准。 这些可能涉及标准的子级别,并且完全取决于您要进行的审查的数量,尤其是当选项彼此非常相似时。
Step 4: Build the Hierarchy from Steps 1 to 3. If you are familiar with graph theory, then you can imagine this to be a directed acyclic graph. The connections between each node implies their consideration in the assessment.
第4步 :从第1步到第3步构建层次结构。如果您熟悉图论,那么可以想象这是有向无环图。 每个节点之间的连接暗示了它们在评估中的考虑。
Step 5: Pair-wise comparison of each criteria and sub-criteria to establish their weights.
步骤5 :成对比较每个标准和子标准以建立权重。
Step 6: Pair-wise comparison of each alternatives against each sub-criteria to establish their weights.
步骤6 :将每个替代方案与每个子标准进行成对比较,以确定其权重。
Step 7: Global summation of all these weights (weighted arithmetic sum) for each alternative and ordering them on the basis of this weighted sum.
步骤7 :每个替代方案的所有这些权重的总和(加权算术总和),并根据该加权总和对其进行排序。
Step 8: Calculate the consistency ratio. This is a measure of how consistent the subjective assessment is, when compared to a table of critical values. If found inconsistent, go back to Step 5.
步骤8 :计算一致性比率。 与临界值表相比,这是主观评估的一致性程度的一种度量。 如果发现不一致,请返回步骤5。
So from these steps, you can see how the process got its name and why it is so popular in terms of its application. Now, let’s have a look at the heart of this process — the quantification of subjective beliefs.
因此,从这些步骤中,您可以了解到该过程的名称以及为什么它在应用中如此受欢迎。 现在,让我们看一下这个过程的核心-主观信念的量化。
评价 (The evaluation)
The key-word of AHP is pair-wise comparison. We all know how difficult it is to compare more than three options at a time. To eliminate this difficulty, Prof. Saaty suggested a pair-wise comparison of alternatives/criteria. And this comparison/evaluation is done by assigning intensities that represent various degree of importance, which he defined linguistically [3].
AHP的关键词是成对 比较 。 我们都知道一次比较三个以上的选择是多么困难。 为了消除这一困难,萨蒂教授建议对替代方案/标准进行成对比较。 并且,通过分配代表各种重要性程度的强度来完成此比较/评估,他用语言定义了强度[3]。
The evaluated/assessed alternatives are compiled into a n x n pair-wise comparison matrix A,for each criteria/sub-criteria/goal [1].
对于每个标准/子标准/目标[1],已评估/评估的备选方案被编译成n x n的成对比较矩阵A。
Here, the wi and wj are the weights or intensities of importance from the previous table. You can immediately see that the assessment matrix is symmetric, making computation easier.
在这里, wi和wj是上表中重要性的权重或强度。 您可以立即看到评估矩阵是对称的,从而使计算更加容易。
Once you create the assessment matrix, the next step is to convert it into vector. This vector encodes the information present in the matrix and is called the priority vector.
创建评估矩阵后,下一步就是将其转换为向量。 该向量对矩阵中存在的信息进行编码,称为优先级向量 。
There are a few ways in which you can calculate this priority vector. One way is to obtain the Perron-Frobenius eigenvector [4], or simply the normalized eigenvector of the matrix. The other way is to calculate the geometric mean of the elements on the respective row divided by a normalization term so that the components of the priority vector eventually add up to 1 [1]. This method is an approximation of the normalized eigenvector method.
有几种方法可以计算此优先级向量。 一种方法是获得Perron-Frobenius特征向量[4],或者简单地获得矩阵的归一化特征向量 。 另一种方法是计算相应行上元素的几何平均值 ,再除以归一化项,以使优先级向量的分量最终加起来为1 [1]。 该方法是归一化特征向量法的近似。
The final step of the assessment is the weighted arithmetic sum of the priority vectors generated for each sub-criterion and ordering them to rank the alternatives.
评估的最后一步是为每个子标准生成的优先级向量的加权算术总和,并对其排序以对替代项进行排序。
一致性比 (Consistency Ratio)
The underlying assumption in AHP is that the decision makers are rational. This basically means that the decision maker is assumed to apply the same subjective beliefs every time for the same problem. However, in reality, this may not be the case. Prof. Saaty took care of this uncertainty by proposing a consistency index, CI
AHP的基本假设是决策者是理性的 。 这基本上意味着,假设决策者每次都针对相同的问题应用相同的主观信念。 但是,实际上可能并非如此。 Saaty教授通过提出一致性指数CI解决了这种不确定性
Where lambda_max is the maximum eigen value of the pair-wise comparison matrix and n is the number of alternatives.
其中, lambda_max是成对比较矩阵的最大特征值, n是替代数。
To scale for different size matrices, the Consistency Ratio was developed, CR
为了适应不同尺寸的矩阵,开发了一致性比率CR
Where, RI_n is an average estimate of the CI obtained from a large enough set of randomly generated matrices of size n. The look-up table for RI_n are given by Prof. Saaty as,
其中, RI_n是从足够大的大小为n的随机生成的矩阵集中获得的CI的平均估计。 萨蒂教授给出了RI_n的查询表,因为
How to use the CR? — According to Prof. Saaty, in practice, one should accept matrices with CR ≤ 0.1 and reject values greater than 0.1. A value of CR = 0.1 basically means that the judgments are 10% as inconsistent as if they had been given randomly. By choosing a lower CR, one could try to reduce this inconsistency, and the only way to do that is to go back and re-evaluate the subjective weights.
如何使用CR? —根据Saaty教授的说法,实际上,应该接受CR≤0.1的矩阵并拒绝大于0.1的值。 CR = 0.1的值基本上意味着判断是10%,就像随机给出的判断一样不一致 。 通过选择较低的CR,可以尝试减少这种不一致,而这样做的唯一方法是返回并重新评估主观权重。
Phew, that was a lot of theory, so let’s get on with its implementation in Python for a simple use-case
哎呀,这是很多理论,所以让我们继续在Python中实现一个简单的用例
在Python中实现AHP (Implementing AHP in Python)
As far as I know there is only one well developed python library out there for AHP — pyAHP, but let’s write the code from scratch using the process described before. Here, I will use a typical use-case from [1] to illustrate the process. (Truth be told, it is pretty easy to implement in Excel!)
据我所知,目前只有一个针对AHP的完善的python库-pyAHP,但让我们使用上述过程从头开始编写代码。 在这里,我将使用[1]中的典型用例来说明该过程。 (说实话,在Excel中实现非常容易!)
Code can be found on my GitHub repository
可以在我的GitHub存储库中找到代码
问题定义 (Problem Definition)
Let’s imagine you want to travel to Europe on a holiday and you plan on visiting a few interesting cities. You have a few cities in mind — Madrid, Hamburg and Paris, but your budget only allows you to visit one of those. To help you get maximum bang for your buck, you decide to use AHP to help you narrow down on a suitable city.
假设您要去欧洲度假,并计划游览几个有趣的城市。 您可能会想到几个城市-马德里,汉堡和巴黎,但是您的预算只允许您访问其中一个。 为了帮助您最大程度地赚钱,您决定使用AHP帮助您缩小适合的城市范围。
目标,标准和替代方案 (Goal, Criteria and Alternatives)
The overall goal is obviously your personal satisfaction. The alternatives are {Rome, Madrid, Paris} and let us imagine you select the following criteria to assess each city — {Climate, Sightseeing, Environment}. Let us build the Hierarchy -
总体目标显然是您的个人满意度。 备选方案是{罗马,马德里,巴黎},让我们想象您选择以下标准来评估每个城市-{气候,观光,环境}。 让我们建立层次结构-
Fig. 3— Hierarchy for use-case (image by author) 图3:用例的层次结构(作者提供的图像)导入库 (Importing Libraries)
Alright, so let's begin the assessment process by importing just two libraries
好了,让我们通过仅导入两个库来开始评估过程
import numpy as np
import pandas as pd创建成对比较矩阵 (Creating pair-wise comparison matrix)
We exploit the symmetric nature of the comparison matrix and take input only for the upper triangular matrix.
我们利用比较矩阵的对称性质,仅对上三角矩阵取输入。
# Number of options
n = 3# Creating default matrix of ones
A = np.ones([n,n])# Running a for loop to take input from user and populate the upper triangular elements
for i in range(0,n):
for j in range(0,n):
if i aij = input('How important is option{} over option{} ?: '.format(i,j))
A[i,j] = float(aij) #Upper triangular elements
A[j,i] = 1/float(aij) #Lower triangular elements Remember, our criteria set was {Climate, Sightseeing, Environment}, so option 0 is Climate, option 1 is Sightseeing and option 2 is Environment. We run this piece of code to generate pair-wise comparison matrix for the criteria weights.
请记住,我们的标准集是{气候,观光,环境},因此选项0是气候,选项1是观光,选项2是环境。 我们运行这段代码来生成标准权重的成对比较矩阵。
How important is option0 over option1 ?: 0.5
How important is option0 over option2 ?: 0.25
How important is option1 over option2 ?: 0.5This can be interpreted as —
这可以解释为-
‘Climate is twice as less important than Sightseeing opportunities and four times less important than the Environment in the city. Sightseeing opportunities are twice as less important than the Environment in the city’
“气候的重要性比观光机会低两倍,比城市的环境重要性低四倍。 观光机会比城市环境的重要性低两倍
Once the matrix is generated, we compute the priority vector by normalizing the eigen vector of the largest eigen value. The elements in this eigen vector are the weights of the criteria.
一旦生成矩阵,我们就可以通过归一化最大特征值的特征向量来计算优先级向量。 该特征向量中的元素是标准的权重。
e = np.linalg.eig(A)[1][:,0]
p = e/e.sum()>>> array([0.14285714, 0.28571429, 0.57142857])The two pieces of code are combined into a function
这两段代码组合成一个函数
def pairwise_matrix(n):A = np.ones([n,n])
for i in range(0,n):
for j in range(0,n):
if i aij = input('How important is option{} over option{} ?: '.format(i,j))
A[i,j] = float(aij)
A[j,i] = 1/float(aij)#Computing the priority vector
eig_val = np.linalg.eig(A)[0].max()
eig_vec = np.linalg.eig(A)[1][:,0]
p = eig_vec/eig_vec.sum()
return p, eig_val We call this function for generating pair-wise comparison matrices and priority vectors for assessing each of the alternative against each criterion. Remember our alternatives set was — {Rome, Madrid, Paris}.
我们称此函数为生成成对比较矩阵和优先级向量,以根据每个标准评估每个替代项。 请记住,我们的替代方案是– {罗马,马德里,巴黎}。
The priority vectors for each of the matrix are —
每个矩阵的优先级向量为-
pr_c = pairwise_matrix(3)[0] #All Criteria
pr_c0 = pairwise_matrix(3)[0] #Criteria 0: Climate
pr_c1 = pairwise_matrix(3)[0] #Criteria 1: Sightseeing
pr_c2 = pairwise_matrix(3)[0] #Criteria 2: Environment#Priority Vector for Criteria 0 pr_c0
>>> array([0.44444444, 0.44444444, 0.11111111])#Priority Vector for Criteria 1 pr_c1
>>> array([0.6, 0.3, 0.1])#Priority Vector for Criteria 2pr_c2
>>> array([0.09090909, 0.18181818, 0.72727273])We also calculate the Consistency Ratio for each of these comparison matrices. For n= 3, the RI_n would be 0.5247. The maximum eigen value across all the matrices was 3. Therefore, by the earlier formula, the CR would be 0 for each of the matrix, which is < 0.1 and hence acceptable.
我们还计算了每个比较矩阵的一致性比率。 对于n = 3,RI_n将为0.5247。 所有矩阵的最大特征值均为3。因此,根据较早的公式,每个矩阵的CR均为0,该值<0.1,因此可以接受。
The final step is to get their weighted arithmetic sum to yield the rank vector
最后一步是获取它们的加权算术和以得出秩向量
r = pr_c0*pr_c[0] + pr_c1*pr_c[1] + pr_c2*pr_c[2]
print(r)>>> [0.28686869 0.25310245 0.46002886]The weighted arithmetic sum for Paris is much higher than Rome or Madrid, so it is assigned rank1, followed by Rome and Madrid.
巴黎的加权算术总和远高于罗马或马德里,因此被分配为等级1,其次是罗马和马德里。
There you go! With the help of AHP, you successfully managed to quantify your subjective analysis and decided to fly to Paris!
你去! 在AHP的帮助下,您成功地量化了您的主观分析,并决定飞往 巴黎 !
结论 (Conclusion)
The major flaw with AHP is the rank reversals of alternatives when evaluated by a different group of people. The other issue is with the philosophical basis of including it in operational research.
层次分析法的主要缺陷是当由不同人群评估时,替代方案的排名逆转。 另一个问题是将其纳入运筹学的哲学基础。
Having said that, AHP is still a popular MCDM method and relatively easy to implement and interpret. Apart from python, there are a few commercial softwares such as SuperDecisions that help you create the hierarchy and perform pairwise evaluations.
话虽如此,AHP仍然是一种流行的MCDM方法,并且相对易于实现和解释。 除python外,还有一些商业软件,例如SuperDecisions,可帮助您创建层次结构并执行成对评估。
There are many more MCDM methods to cater to the shortcomings of AHP and are more advanced in terms of their mathematical foundations. Some that come to mind are PROMETHEE, TOPSIS, etc.
有更多的MCDM方法可以解决AHP的缺点,并且在数学基础上更先进。 我想到的一些是PROMETHEE,TOPSIS等。
I hope you found this post helpful and feedback is always appreciated!
希望本文对您有所帮助,并希望您能给予宝贵的反馈!
Ciao!
再见!
翻译自: https://towardsdatascience.com/deep-dive-into-analytical-hierarchy-process-using-python-140385fabaa1
python层次分析