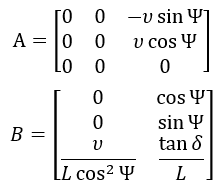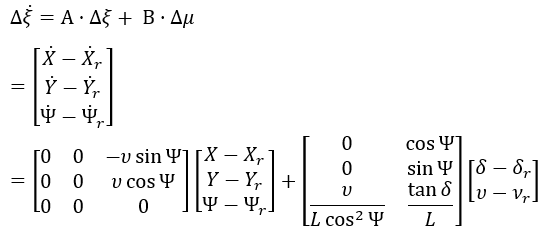无人驾驶车辆模型预测控制_【无人驾驶】车辆运动学模型验证及其线性化、离散化...

一、车辆运动学模型验证

上一篇文章我们得到车辆的运动学模型之后，就可以通过 Carsim/Simulink 联合仿真来验证车辆运动学模型的准确性， Simulink 模型如下图，车辆轴距 L 设置为 2.6m 。

输入量前轮转角delta和车速velocity如下图：

输出结果对比如下图：

可以看出，车辆的运动学模型与实际车辆的运行状态基本相符，证明运动学模型的可靠性。 s-function模块程序如下：

function [sys,x0,str,ts,simStateCompliance] = check(t,x,u,flag)switch flag,  case 0,    [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;  case 1,    sys=mdlDerivatives(t,x,u);  case 2,    sys=mdlUpdate(t,x,u);  case 3,    sys=mdlOutputs(t,x,u);  case 4,    sys=mdlGetTimeOfNextVarHit(t,x,u);  case 9,    sys=mdlTerminate(t,x,u);  otherwise    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));endfunction [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizessizes = simsizes;sizes.NumContStates  = 0;sizes.NumDiscStates  = 3;   %输出量X、Y、Yaw为离散量，设置为3sizes.NumOutputs     = 3;   %输出量数量sizes.NumInputs      = 2;   %输入量数量sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys = simsizes(sizes);x0  = [-450;-450;0];    %初始车辆状态str = [];Ts=0.05;    %采样时间ts  = [Ts 0];simStateCompliance = 'UnknownSimState';function sys=mdlDerivatives(t,x,u)sys = [];function sys=mdlUpdate(t,x,u)Ts=0.05;    %采样时间L=2.6;  %车辆轴距sys = x+[cos(x(3));sin(x(3));tan(u(1))/L]*u(2)*Ts;  %验证车辆运动学模型function sys=mdlOutputs(t,x,u)sys = [x(1);x(2);x(3)];function sys=mdlGetTimeOfNextVarHit(t,x,u)sampleTime = 1; sys = t + sampleTime;function sys=mdlTerminate(t,x,u)sys = [];

有了上述的运动学模型之后，我们就可以通过它对车辆进行控制，但由于之前建立的车辆运动学模型是一个非线性的模型，在满足设定情况下对非线性模型的求解也十分复杂，而且在实际工程中，各种非线性模型千奇百怪，对其的解法也就不唯一。因此，对于非线性模型的线性化是一种通用的模型简化求解方式，套用知乎上看到的一句话“非线性化模型线性化之后，一切跟着套路走”。 二、 泰勒展开式

背景：泰勒展开式可以看作是将一条曲线在某一点处，将其用多项式来表示，只要其一阶导、二阶导···n阶导都和原曲线相同即可。

公式：

延伸： 泰勒级数、泰勒公式、泰勒展开式、多元函数泰勒展开式。

三、车辆运动学模型线性化

假设如下一阶线性微分方程

并且在点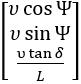 处满足 ，对该点进行泰勒展开，忽略二阶及以上高阶项，得：

移项可得：

令

便可得到如下线性方程形式：

将车辆运动学模型在 ， 进行线性化， 为 输入变量，得：

其中 ， ， 分别对应车辆运动学模型中的 ，因此求得：

综上，车辆运动学模型的线性方程组可以写为：

四、车辆运动学模型离散化

离散化其实也是对模型的一种简化，虽然运算数据会变得很多，但变为了离散化模型之后对非线性模型的描述也会更加贴合一些。 此处进行近似离散化，将 和 均看做时间的函数，线性方程组可以写作：

所以：

其中： 为时间间隔； I为单位矩阵。

  至此完成对车辆运动学模型的离散化，依据上述公式便可以控制车辆对期望轨迹进行跟踪。

五、延伸

  近似离散化、精确离散化、轨迹跟踪、路径跟踪