【PET图像重建】基于小波变换的PET图像重建matlab仿真

1.软件版本

matlab2013b

2.本算法理论知识

《基于模糊理论和小波变换的PET图像重建》

3.部分源码

function y=func_image_recon(image_1D,N,NUM,im2,wl);

Len = length(image_1D);                   
im   = image_1D;                        
y   = zeros(1,Len);  
%得到低通滤波器
h   = [0.48296,0.83652,0.22414,-0.12941]; 
%进行N级恢复处理

[r,c]                 = size(image_1D);
%im为二维小波变化之后的小波域数据
wl                    = im;
Cl                    = im2./wl;
Cl(isnan(Cl) == 1)    = 0;
Cl(isfinite(Cl) == 0) = 1;
%获得概率矩阵A
A = rand(r,c);

%定义观测模型
e = rand(r,c);
P = A.*Cl.*wl;




for i=N:-1:1;         
    %N级平滑分量
    im1    = im(1,1:Len/2^(i));             
    im1    = dyadup(im1);    
    %去掉0
    im1    = im1(1,[1:length(im1)-1]);      
    s2     = im(1,(Len/2^(i)+1):Len/2^(i-1));
    %插零值处理
    s2     = dyadup(s2);                  
    s2     = s2(1,[1:length(s2)-1]);     
    hn_fft = [h,zeros(1,(length(im1)-length(h)))]; 
    gn_fft = [h(1,2),-h(1,1),zeros(1,(length(s2)-length(h))),h(1,4),-h(1,3)]; 
    
    hrcon  = hn_fft(end:-1:1);                         
    grcon  = gn_fft(end:-1:1);
    
    hrcon  = circshift(hrcon',1)';           
    grcon  = circshift(grcon',1)';   
    %fft
    c      = ifft(fft(im1).*fft(hrcon));      
    d      = ifft(fft(s2).*fft(grcon));      
    %图像重建
    
    
    for jj = 1:NUM
        if jj == 1
           w(:,:,1)                = (c + d);   
        else
           w(:,:,jj)               = w(:,:,jj-1) - 0.2*( (im(1,1:Len/2^(i-1),jj-1) - w(:,:,1)) - 0.0002*sign(wl)); 
        end
         im(1,1:Len/2^(i-1),jj)    = w(:,:,jj);  
    end
    
    ims(1,1:Len/2^(i-1)) = w(:,:,NUM); 
    
end

y=ims;                            

对应的代码简要说明：

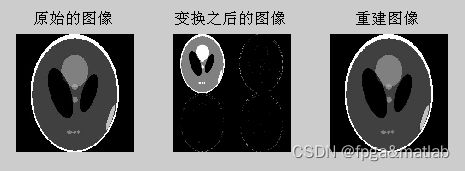
这个部分对应的小波分解，通过一维快速变换得到最终的二维变换效果。

这个就是PET迭代重构。

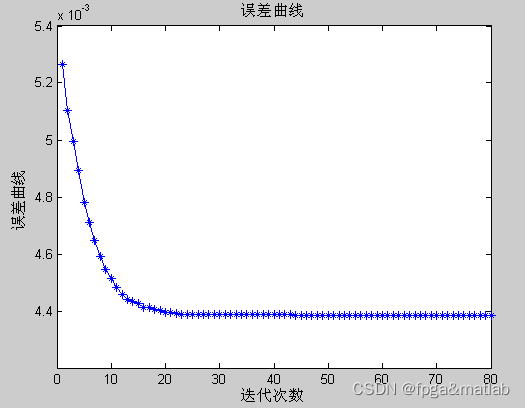
最后的误差曲线。

4.仿真结论

5.参考文献

[1]黄慧. 基于模糊理论和小波变换的PET图像重建[D]. 东南大学, 2006.A09-23