【深度学习】：《PyTorch入门到项目实战》第10天：梯度爆炸、梯度消失、梯度检验

【深度学习】：《PyTorch入门到项目实战》第10天：梯度爆炸、梯度消失、梯度检验

• ✨本文收录于【深度学习】：《PyTorch入门到项目实战》专栏，此专栏主要记录如何使用PyTorch实现深度学习笔记，尽量坚持每周持续更新，欢迎大家订阅！
• 个人主页：JoJo的数据分析历险记
• 个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 如果文章对你有帮助，欢迎✌关注、点赞、✌收藏、订阅专栏

参考资料：本专栏主要以沐神《动手学深度学习》为学习资料，记录自己的学习笔记，能力有限，如有错误，欢迎大家指正。同时沐神上传了的教学视频和教材，大家可以前往学习。

• 视频：动手学深度学习
• 教材：动手学深度学习

写在前面

训练神经网络时，尤其是深度神经网络所面临的一个重要问题就是梯度爆炸或梯度消失，也就是我们训练神经网络的时候，导数或梯度有时会变得非常大，或者非常小，甚至于以指数方式变小，这加大了训练的难度。接下来我们介绍一些什么是梯度爆炸和梯度消失。

为了方便演示，这里我们假设每一层神经网络只有两个神经元，每一层神经网络的参数为$W^{[L]}$,假设激活函数就是线性的$g(z)=z$，并且令$b=0$，每一层的输出结果为$a^L$,做好上述假设后，我们可以得到下述关系:
$a^1=W^{1}X,a^2=W^2{a}^1,...,a^L=W^L{a}^{L-1}$，进一步可以导入计算y
$$y=W^L{W}^{L-1}...W^{1}X$$
此时相当于有很多层权重矩阵乘积在一起，假设所有的矩阵都是1.5倍的单位矩阵，那么当层数很多时$1.5^L$将会很大，意味着y会以指数爆炸增长，同样意味着梯度也会很大。相反，假设矩阵是0.5倍的单位矩阵，那么y会以指数趋于0.同样意味着梯度也会消失。假设有50层：
$$1.5^{50}=637621500,0.5^{50}=8.88\times 10^{-16}$$
可以看出，在深度神经网络中，如果不进行相应的处理设置，很容易出现梯度爆炸或梯度消失

1.梯度消失

我们在之前介绍了sigmoid激活函数，但是它现在不常用了，因为他就是导致梯度消失的一个常见的情况。现在我们来看看sigmoid的梯度情况

%matplotlib inline
import torch
import matplotlib.pyplot as plt
from torch import nn
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
y.backward(torch.ones_like(x))

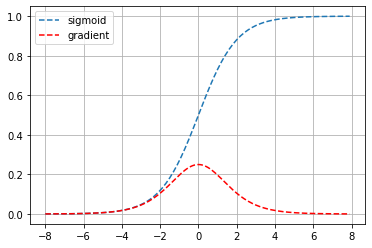
plt.plot(x.detach().numpy(), y.detach().numpy(),'--',label='sigmoid')
plt.plot(x.detach().numpy(), x.grad.numpy(),'r--',label='gradient')
plt.legend(loc = 'best')
plt.grid(True)

​

​

可以看出，当sigmoid函数的输入很大或是很小时，它的梯度都会消失。 此外，当反向传播通过许多层时， 这些地方sigmoid函数的输入接近于零，可能导致整个乘积的梯度可能会消失。因此，ReLU激活函数成为了大家默认的选择

2.梯度爆炸

同样的，梯度爆炸也是一个非常严重的问题，它会让导致梯度下降很难收敛。下面我们举一个简单的例子，来看看梯度爆炸的情况，我们定义一个4×4的随机矩阵，满足标准正态分布，观察乘以50次之后的结果

M = torch.normal(0, 1, size=(4,4))
print('一个矩阵 \n',M)
for i in range(50):
    M = torch.mm(M,torch.normal(0, 1, size=(4, 4)))

print('乘以50个矩阵后\n', M)

一个矩阵 
 tensor([[ 1.2106, -1.2478,  0.9032,  0.1750],
        [-0.4060,  0.7475, -2.2134, -2.1323],
        [-1.0121,  0.1883,  1.7743, -0.6649],
        [ 0.1302,  0.2794,  0.0039, -0.2880]])
乘以50个矩阵后
 tensor([[-6.4536e+12,  2.9500e+11, -3.1643e+12,  3.2686e+12],
        [ 4.9242e+12, -2.2509e+11,  2.4144e+12, -2.4940e+12],
        [-1.8533e+12,  8.4715e+10, -9.0872e+11,  9.3866e+11],
        [-6.2537e+11,  2.8586e+10, -3.0663e+11,  3.1674e+11]])

可以看出经过五十次矩阵相乘之后，数值达到了$10^{11}-10^{12}$

在很长一段时间内，梯度爆炸和梯度消失曾是训练深度神经网络的阻力，但是选择初始化权重是解决该问题的有用的方法。

3.初始化权重

正如我们刚刚所说的，sigmoid激活函数容易导致梯度消失，因此，一个比较常用的方法是使用ReLU函数来当做激活函数，降低了梯度消失和爆炸问题。解决上述问题的另一种常用的方法是进行参数初始化。一个比较常用的方法就是$Xavier$初始化。它假定方差为:$\sqrt{\frac{2}{n^{[l-1]}+n^l}}$，还有人用tanh函数，使用$\sqrt{\frac{1}{n^{l-1}}}$,如果使用ReLu激活函数，有些作者建议使用 $\sqrt{\frac{2}{n^{l-1}}}$.实际上，我觉得所有这些公式只是一个调整的选择，它们给出初始化权重矩阵的方差的默认值，如果想添加方差，方差参数则是另一个我们需要调整的超参数。下面我们来看看如何实现初始化权重

"""定义一个神经网络"""
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
"""正态分布初始化"""
def norm(m):
    if type(m) == nn.Linear:#对线性层进行初始化权重
        nn.init.normal_(m.weight, mean=0, std=0.01)#正态分布初始化
"""Xavier初始化"""
def Xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(n.weight)#Xavier初始化
net[0].apply(norm)#对第一个线性层进行正态初始化
print(net[0].weight)
net[2].apply(Xavier)#对第二个线性层进行Xavier初始化
print(net[2].weight)

Parameter containing:
tensor([[ 2.6455e-03, -9.4835e-03, -2.3148e-03,  7.3588e-03],
        [ 8.4367e-03, -6.8525e-03,  4.5711e-03,  6.6946e-04],
        [-1.7318e-03, -2.4081e-03, -5.8394e-03,  4.2219e-03],
        [-8.6585e-03,  1.5090e-02,  1.2062e-02,  4.7167e-03],
        [ 8.8256e-03, -7.8020e-05, -1.7378e-03, -2.5176e-02],
        [-1.1565e-02,  1.7698e-03, -1.8693e-02,  8.1501e-05],
        [-1.3891e-02, -6.1892e-03, -4.7369e-03,  9.8099e-03],
        [ 3.5225e-04,  4.4494e-03, -2.1365e-03,  4.0189e-03]],
       requires_grad=True)
Parameter containing:
tensor([[ 0.1272,  0.1947, -0.1398, -0.0676,  0.1016, -0.2671, -0.1270, -0.3072]],
       requires_grad=True)

4.梯度的数值计算

在实施backprop时，有一个测试叫做梯度检验，它的作用是确保backprop正确实施。因为有时候，我们不能保证我们写的程序是完全正确的。为了实现梯度检验，我们首先说说如何计算梯度的数值逼近。假设给定一个函数$f(x)=x^3$,根据数学分析中的知识，它的导数为$f^{\prime }(x)=3x^2$。根据微积分的知识，我们可以通过以下方式来逼近梯度，给定一个任意小的$ϵ$，有：
$$f^{\prime }(x{)}_{approx}\frac{f(x+ϵ)-f(x-ϵ)}{2ϵ}$$
假设$x=1,ϵ=0.01$，则有：$f^{\prime }(x)=3$,$f^{\prime }(x{)}_{approx}=\frac{1.01^3-0.99^3}{2\times 0.01}=3.0001$,可以看出误差为0.0001，实际上，对于给定的一个$ϵ$，导数的逼近误差是$O({ϵ}^2)$.有了这个基础，我们下面来看看如何进行梯度检验

5.梯度检验

梯度检验可以帮我们节省很多时间，接下来，我们看看如何利用它来调试或检验backprop的实施是否正确。假设网络中含有下列参数，$W^{[1]}$和$b^{[1]}$……$W^{[l]}$和$b^{[l]}$，为了执行梯度检验，首先要做的就是，把所有参数转换成一个巨大的向量数据，我们要做的就是把矩阵$W$转换成一个向量，把所有$W$矩阵转换成向量之后，做连接运算，得到一个向量参数族$\theta$，该向量表示为参数$\theta$，损失函数$J$是所有$W$和$b$的函数，现在我们得到了一个$\theta$的损失函数$J$（即$J(\theta )$）。接着，得到与$W$和$b$顺序相同的数据，同样可以把$d{W}^{[1]}$和${db}^{[1]}$……${dW}^{[l]}$和${db}^{[l]}$转换成一个新的向量。

接下来对每个参数也就是对每个$\theta$组成元素计算$d{\theta }_{\text{approx}}[i]$的值，使用刚刚介绍的梯度逼近。

$$d{\theta }_{\text{approx}}\left[i\right]=\frac{J\left({\theta }_1,{\theta }_2,\dots {\theta }_i+\epsilon ,\dots \right)-J\left({\theta }_1,{\theta }_2,\dots {\theta }_i-\epsilon ,\dots \right)}{2\epsilon }$$

根据上文的介绍我们知道（$d{\theta }_{\text{approx}}\left[i\right]$）应该逼近$d\theta \left[i\right]$=$\frac{\partial J}{\partial {\theta }_i}$，$d\theta \left[i\right]$是代价函数的偏导数，然后我们需要对i的每个值都执行这个运算，最后得到两个向量，得到$d\theta$的逼近值$d{\theta }_{\text{approx}}$，它与$d\theta$具有相同维度，它们两个与$\theta$具有相同维度，我们实际要做的就是验证这些向量是否彼此接近。具体计算公式如下：
$$check=\frac{{||d{\theta }_{\text{approx}}-d\theta ||}_2}{||d\theta |{|}_2+||d{\theta }_{approx}|{|}_2}$$
具体怎么判断是否足够接近呢，这里要取决于我们选取的$ϵ$，假设选取的$ϵ=10^{-5}$,如果上述得到的值为$10^{-5}$或者更小，那么结果很好，如果为$10^{-3}$，那么需要注意，可能这个值有问题。如果更大的话我们要考虑是否程序存在问题，需要检查一下。
本章的介绍到此介绍，如果文章对你有帮助，请多多点赞、收藏、评论、关注支持！！