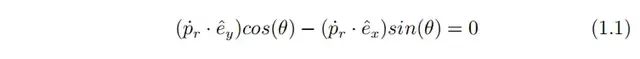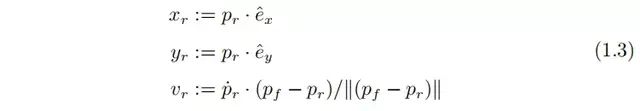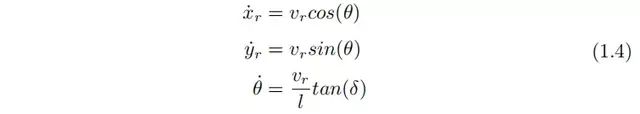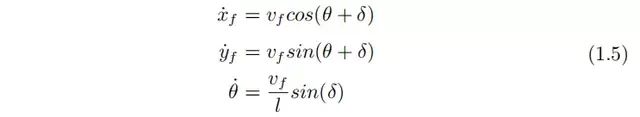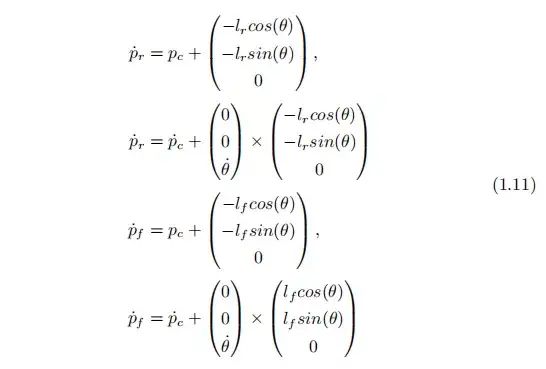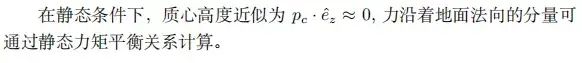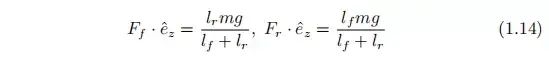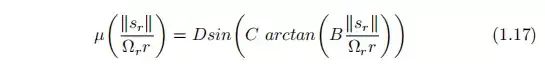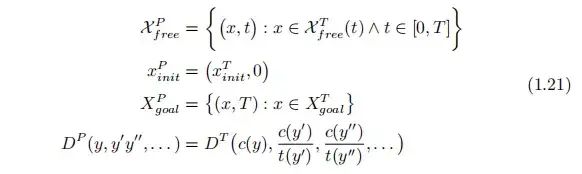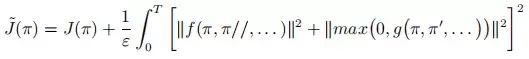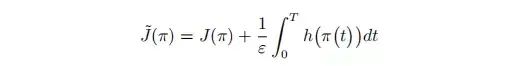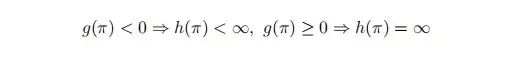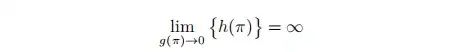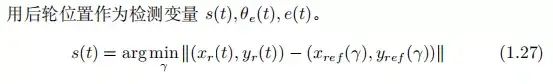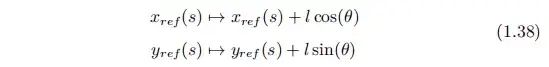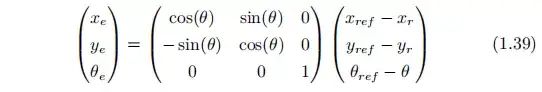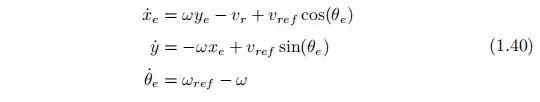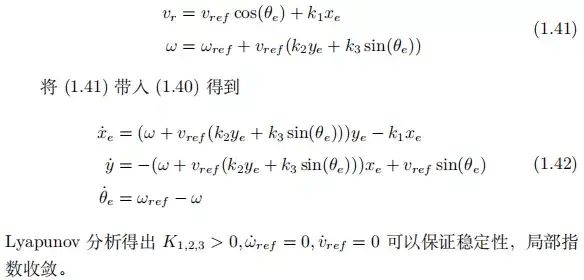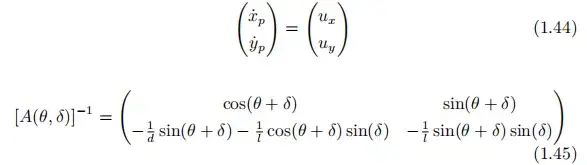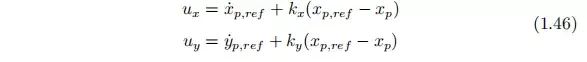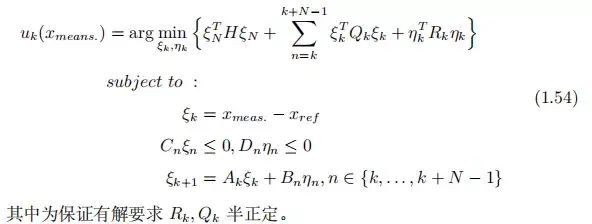数据分析综述:一文带你详细了解自动驾驶技术
©作者 | Alex
美国一项交通事故数据的分析得出:94% 的交通事故责任在驾驶员,其中 31% 由于疏忽,10% 由于注意力不集中。
巨大社会效益意味着巨大的社会需求,过去 30 年学术界和工业界持续不断的增加对无人驾驶领域的投入,近年来传感器、计算技术的突破引起了引燃了这个行业。
从各项赛事到车企的运营,我们似乎看到自动驾驶正逐渐走入现实。
100 年漫长的历史
自动驾驶技术器其实并非新事物,二是已经走过了 100年漫长的历史,早在 1920 年代就已经提出,直到1980 Ernst Dickmanns领导的工作 PROMETHEUS project 为后续的发展铺平了道路,令其看起来可行。
1994 VaMP 无人驾驶车在 95% 时间无人干预情况下,完成了 1600km 旅程,CMU NAVLAB在1995 年 98% 时间无人干预情况下更是行使了500km穿越美国。
接下来是各种挑战赛:2004 年 DARPA Grand Challenge,要求车辆完成 150-mile 越野赛,遗憾的是参赛的15辆车都没有完成任务。2005 年相似的任务,23 支队伍 5 支抵达终点。2007 年DARPA Urban挑战赛 6 只队伍完成比赛,证明在城市环境下自动驾驶的可行性。之后不断有各种大事件和挑战赛举办,同时研究不断深入和加速。
Google 自动驾驶车辆和 Tesla 已经在商业上取得巨大成功。国内自动驾驶也如火如荼。
关于自动驾驶的自动化程度
SAE J3016 给出一个标准,将车辆自动驾驶的程度分为 0-5 个级别,
● 0-人类驾驶。
● 1-只有辅助自动驾驶,包括自适应巡航控制 + 反锁死制动系统 + 电子稳定控制。
● 2-高级辅助功能,如风险最小化,紧急制动。
● 3-系统可以监控环境,可实现某种条件下的完全自动驾驶,但需要驾驶员在超过规定范围时接管驾驶权。
● 4-在某些情况下可以自动驾驶,在需要干预的时候即使驾驶员不能够接管车辆也可以保证车辆安全。
● 5-在所有模式下自动驾驶。
不只是驾驶
无人驾驶走向现实离不开成熟的环境,车载硬件计算能力和无线通信能力使得车辆间可以交换信息,车辆与道路基础设施之间可以通信,并由此带动新的研究领域比如交通安全、效率、信息协调、智慧城市等。
本文将话题限制在决策、运动规划、车辆控制三个方面。
01 决策
无人驾驶车辆本质上是基于观测数据流和先验只是的决策系统,观测数据来自: 车载雷达、激光雷达、相机、GPS/INS 、里程计。
这些观测结合从路网获取的先验知识:交通规则、车辆动态及传感器模型–判断车辆状态、环境状态,做出规划、决策,控制车辆运动。
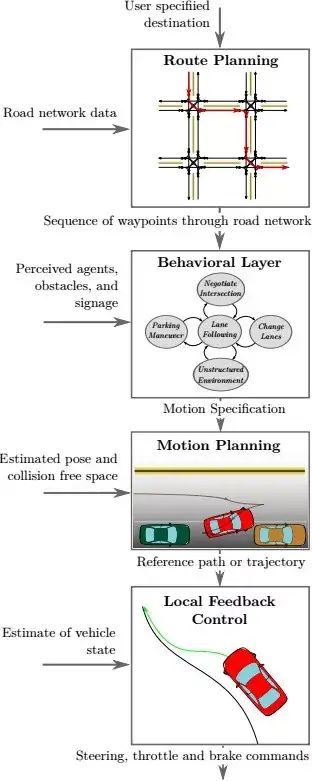
图 1.1: 无人驾驶决策层次
决策包含 4 个层次
● 根据路网决定从当前位置去往目的地,需要经行的路线。
● 根据交通规则指定局部驾驶任务。
● 选择连续路径并通过环境局部导航。
● 修正运动规划的执行误差。
1.1 A. 路线规划
实现自动驾驶首先要通过路网确定当前位置并选出去往目的地的路线。将路网表示为有向图,边表示为通过路段的代价。通过选择最小代价总和,选出行车路线。
这样的表示可能存在几万条边,可以通过 Dijkstra 或 A* 寻找最短路径不太实用。有效的路径规划算法–如何在大陆规模的路网中,经过预处理,以毫秒的时间消耗返回最优路径是一个研究热点。
1.2 B. 行为决策
确定了驾驶路线后,Behavioral 层的作用是在任意时刻感知其他交通参与者的行为、基础设施信号、并遵守交通规则选择驾驶行为。
驾驶手册明确规范了驾驶上下文中的操作。因为上下文环境和可操作行为可以建模为有限集合。自然可将每种行为建模成有限状态机。
一些车队 (如 DARPA Urban challenge 很多参赛队) 将针对各种场景的有限状态机和启发式规则作为行为决策的依据。真实驾驶环境中其他交通参与者的行为、意图存在很多不确定性。
应对这些不确定性是行为决策层要考虑的问题,大量的研究关注交通参与者的意图预测及轨迹估计,如高斯混合模型、高斯过程回归,从传感器数据直接估计意图的基于模型的方法。
这种不确定性通常建模为马尔科夫决策过程 (MDPs)。
1.3 C. 运动规划
行为决策得出驾驶操作如:循线巡航、变道、右转等。行为需要进一步转化为路径或轨迹输入给低层反馈控制器,这些路径或轨迹必须满足:1)对车辆是可行的,2)对乘客是舒适的,3)车载传感器监测无碰撞。运动规划负责选择这样的路径或轨迹。
准确的运动规划解难以计算、通常采用数值近似。最常用的是将问题建模为函数空间的非线性优化,图搜索—将车辆状态空间表示为图。
graph—search 计算最短路径,基于树的方法增量的创建可达状态树,选择最优枝。
1.4 D. 车辆控制
控制车辆稳定的执行运动规划种选择的轨迹,轨迹误差反应了控制的精确性,是反馈控制的依据。
02 规划模型与控制模型
高保真模型-准确反应了车辆响应,更多细节会是规划与控制问题变得复杂。本节只关注一般模型,旨在阐述与模型规划和控制的一般概念。
下文会多次提到车辆的位姿:1 车辆某点位置、车头朝向姿态。通过位姿将车辆运动表示为二维的欧氏空间刚体运动。
2.1 A. 单轨运动学模型
(Single track model) 也是实际应用中最最基本的模型,想象一下自行车。车辆有前后两轮,刚性连接在一起,车轮与地面需要保持接触,每个轮可以围绕各自轴自由旋转。前轮有围绕纵轴旋转的自由度,该纵轴垂直于运动平面 (前轮转向)。
图 1.2: 单轨运动学模型
这种模型除了两轮同步向前无法进行单向整体平移。这种可操作性的局限被称作nonholonomic constraint–是关于哪些方向不能走的约束,属于速度约束–微分约束。
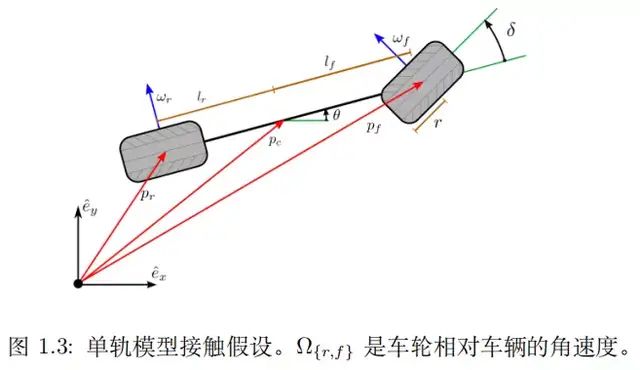
如图 (1.2) 车辆在静止状态下,惯性坐标系基向量(ˆex, eˆy, eˆz),前后轮位置pf,pr, 车辆方向用角度θ等于eˆx与 pf ,−pr夹角表示。
前后轮必须满足共线及与地面接触的约束:
1.后轮与地面接触约束定义:
2. 前轮与地面接触约束定义:
车轮与地面接触约束用惯性坐标系基向量的参数表达形式:
或着用前轮的运动表示:
通过前轮的运动表示微分约束
前、后轮速度之间满足模型规划与控制的主要内容包括选择舵角 (或方向盘角度或转向角度等),舵角的可行范围:
简化方案:用转向角速度 ω 代替舵角 δ
单轨模型适用于做低速路径规划。与接触约束相比惯性影响比较小可忽略。此模型的主要缺点是允许瞬时舵角的改变在运动规划中会引起一些问题。
舵角的连续性要求可通过数据增广 (1.5) 添加。
这样做的缺点就是模型维度变大,从而使运动规划与控制变得复杂。局部坐标系可以选择车轮或质心等。
2.2 B. 惯性效果
车辆加速度足够大时,车轮与地面接触的约束可能被违反。此时将车辆看作整个刚体满足动量定律。加速度与地面给轮胎的反作用力成比例。
![]()
于是前、后轮、质心的速度之间的动力学关系如下:
法向力可用于计算对后轮胎的牵引力
对前轮的牵引力
牵引力抵消摩擦力,摩擦力和接触面法线方向的压力成正比,公式 (1.11)- (1.16) 得出车轮上施加的净力的表达式
由旋转对称 (1.16) 和 (1.17) 的最大值可以得出车辆在能够施加的最大法线力,这个峰值也被称为摩擦锥。
上述模型在自动驾驶中适用频繁。更底层的电子可靠控制、底盘、悬挂支撑需要更精细复杂的模型。
03 运动规划
在行为层计算出车辆的目标位姿,如:行使前方几米远处当前车道的中 心点;或下一个十字路口停车线的中心点;或某个理想的停车场。
运动规划层主要功能是计算到达目标点的安全、舒适、可执行的轨迹。同时接收车辆附近的静止或运动的障碍物信息,以确保路径或轨迹符合动力学和运动学约束,并且安全平稳无碰撞。
很多时候,运动规划过程实质上是最小化一个给定的目标函数。除交通时间外,目标函数惩罚冒险的行为或 使乘客不舒服的行为。
另外运动规划的输出会反馈到控制层,校准车辆运动 以符合运动规划。车辆运动规划的结果可以是一段路径也可以是轨迹。
在路径规划返回一个函数
3.1 A 路径规划
算法复杂度
过去几十年可行解和优化解都已经被充分研究了,其中算法的复杂度深受关注,由于算法是NP-hard,于是人们转向寻求近似解,或在某些子集中求解。
概括的看
在没有障碍物的特定环境下,存在曲率约束的 path,计算可以很高效。大多数情况下没有实用的精确算法,只能求助于数值解。算法的性能取决于问题的定义和人们对收敛速度的要求。
数值解大致分为 3 大类:
变分法
变分法将 path 作为有限维向量的函数,通过非线性连续优化可快速收敛到局部最优解。需要好的初值才能收敛到全局最优解。
Graph-search 图搜索
通过将位姿空间表示成离散的图,在所有路径中寻找代价最小的。不容易陷入局部极小解,但只适用有限路径搜索。
Incremental search 增量搜索方法
采样可行位姿空间,逐步建立可达图 (通常是树结构),维护可达位姿的离散集合,一旦图足够大,就会有一个节点位于目标区域,理想路径可通过跟踪从当前位姿节点到目标节点的边。
可以将这些方法结合在一起使用:可先通过一次粗糙的Graph-search 猜测一个初值,再使用变分法求解。
3.2 B. 轨迹规划
动态环境或有动态约束的运动规划问题适合用轨迹规划的框架来解决。
复杂度
动态环境的轨迹规划是静态环境的 path 规划的泛化,所以也是一个 PSPACE-hard 的问题,相比于 path 规划,trajectory plan 轨迹规划更加难以解决。
非平凡轨迹规划的精确解无法求取,人们同样寻求数值解,在增加了时间维度后,轨迹规划问题可以转化为 path 规划问题。
同时轨迹和路径的位姿间存在映射:
按照可以处理微分约束的 path 规划的求解方法,再将结果转化为轨迹形式就可以了。
3.3 C. 变分方法
如上文所述路径规划问题可以看作是单位时间间隔的轨迹规划问题,所以在此通称为轨迹规划。
轨迹优化是一个非线性连续优化问题,首先将无穷维函数空间投影到有限维的向量空间,把问题 (1.22) 该写为:
其中 holonomic(位姿约束) 和微分约束 (速度约束等) 表示为相等或小于的约束条件。某些应用中使用惩罚函数将约束优化问题松弛后编程无约束优化问题。
代价函数变为
在不等式约束中代价函数变为
代价函数满足
这些代价函数背后的直觉之要 ε 足够小,代价函数的极小值就会接近原始的代价函数极小值。这类算法的共性是容易陷入局部极小,需要好的初始值。
不过总会有解就是了。其中可以通过坐标变换把车轮与地面接触的约束转变为线性约束。给定车辆模型和路段可以有效的计算出耗时最少的轨迹。
这类方法有两个子类:
直接法
直接法将近似解限定在 Π(X , T) 有限维子空间中,假设
间接法
就是直接求解常微分方程。可以采用变换自由初始条件直到能够积分到理想的终止状态。这种方法被称为瞄准方法 (shooting method),很形象。
另外变分方法还有很多,上面只是简短描述一二。
3.4 D. 图搜索
1). 车道线图
(Lane Graph)一个足够好的车道线图包括可以循线行使的路径且路径之间互相连接。车道线图可以是高层街道网络地图加部分人工标注。
图 1.6: 手绘有驾驶路径
大多数情况下只要求车辆顺着车道线行使,但是在路网设计的时候没有考虑到的障碍或路网图没有覆盖的区域,车辆需要具备导航功能。
比如在道路中间出现抛锚的车辆,就需要避开障碍物,保证车辆安全通过。
解决方案 (根据如何表示障碍物) 大致分为两大类:
1)几何 (组合方法),障碍物表示为多边形或多面体。
2) 回避如何表示障碍物,转为判断给定的路径是否 与障碍物碰撞,称为采样的方法。
2). 几何方法
如前所述,可达位姿表示为图上的节点,节点之间的边对应连接两个位姿的路径。
对于有最大曲率约束的路径规划问题是NP-hard 的,已经有多项式复杂度的算法能够得出近似解。
3). 基于采样的方法
变分法难以避免陷入局部最优,然而计算代价比较大。路径规划问题的复杂性,远非曲率约束能够概括,基于图的方法不够用来处理复杂的状况。
人们转而考虑基于采样的方法,仅仅探索位姿是否可达,以及路径上是否存在障碍。
图 1.7: 有网格/无网格 的基元图
(a)90 度左转圆弧、90 度右转圆弧、直线
(b)89 度左转圆弧、89 度右转圆弧、直线
由于分支在原点形成环,所以最终是树而不是网格状的,覆盖面积比较小。
图 1.8: 递归生成 roadmap
从 X 中产生离散样本集覆盖 X,连接他们中的可行路径得到。
图 1.9: 基于采样的 Roadmap Construction
这类方法基本遵循上述流程,区别在于采样点数 (X , n) 和邻域 (x, V ) 的选择。新的算法总是不断涌现。
4).Graph Search Strategies
前面三小节 (1.3.4),(1.3.4),(1.3.4) 是关于如何建立图,本节是关于如何搜索路径。
最著名的路径搜索算法 Dijkstra,算法通过将一个点到所有其他点的最短路径建成树结构。
如果只有一条路径可用,人们会采用启发式搜索,最著名的 A*,还有加权 A*。及根据传感器部分更新path 的 D*、Focussed D*、D* Lite 算法等等,新的算法层出不穷。
3.5 E. 增量搜索策略
对固定图的搜索,可能无法返回可行路径或只能得到次优解。增量搜索则可为 X 建立越来越精细的图,同时在每一级判断是否存在可行路径。本质上是提供一系列路径,这些路径质量越来越高逐步接近最优路径。
缺点是不同分辨率的图上互相独立进行路径规划,缺乏对信息的重用;还有以多快的速度增加分辨率、如何增加节点都需要考虑。为解决这些问题通常将增加离散度和路径规划集成在一个过程中完成。
增量路径规划从起始位姿开始向外生成一棵树 (explore the X 空间),探索行为是指从树中随机选择一个点,展开这个点是指从这个点开始执行驾驶函数 (1.3.4),当这棵树足够大的时候,会找到从初始位姿到目标位姿的路径。
代表算法如 expansive spaces tree(EST),Rapid-exploring Random Trees(RRT),及改进 RRT 的 RRT*。
图 1.10: incremental tree-based algorithm
3.6 F.Practical Deployments
上面列举的 motion plan 都有实际应用的案例,且各车队采用的方案有很大不同。
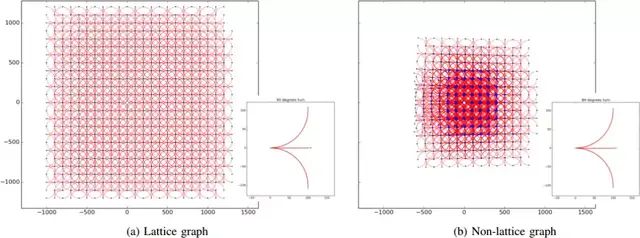
● CMU’s BOSS vehicle: 变分法 +lattice graph+ anytime D*
● runner-up vehicle:search strategy+ Hybrid A* + motion primitives
● VictorTango :graph discretization of possible maneuvers + A* search
● MIT:RRT
04 车辆控制
路径规划 (1.3.1) 和轨迹规划 (1.22) 之后, 需要车辆稳定地沿着给定的路径、轨迹行使。
常用的反馈控制原则
其中反馈函数是关于参考路径上的最近点的函数。如果路径自相交或不可微那么闭环向量 f(x, u(x)) 就不能保证连续,进而导致不可预料的问题。轨迹控制比较直接,但是会受控制器操作的限制。
多数情况下,分析轨迹稳定性可以归结为判断时变系统的原点的稳定性。Lyapunov 理论的基本形式只适用于时不变系统。
时变系统的稳定性指标包括:
● 一致渐近稳定性:上面条件 1) 中,δ 独立于 t1。
● 指数稳定性:衰减速率有指数形式的上确界。
可以看到到控制器表示为时间趋近无穷时的轨迹误差。而实际应用中,轨迹是有限的,因此需要考虑到系统的过渡状态的响应。
4.1 A. 动力学模型的路径稳定性
pure pursuit 轨迹追踪
轨迹追踪及其变种算法,易于部署且性能可靠。
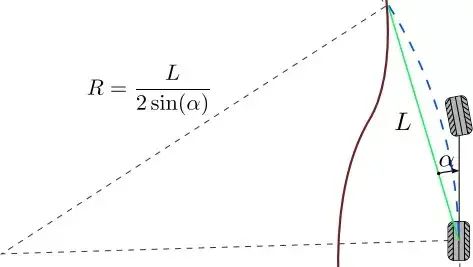
图 1.11: pure pursuit: 在后轮和参考路径 (褐色线) 拟合一个圆 (蓝 色),从后轮向前 L 距离 (圆上弦长),圆在这点与车辆前进方向相切
从车辆当前位置前进方向一个观测半经 L 与路径有一个交点,穿过此交点和车辆当前位置拟合一个半圆,在交点处与车辆前进方向相切。
圆的曲率满足
基于后轮位置的反馈
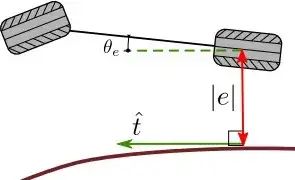
图 1.12: 后轮反馈控制
跟随误差:
t 时刻路径 s(t) 点切向量
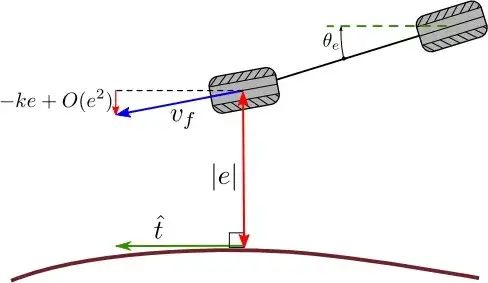
基于前轮位置的反馈
图 1.13: 前轮反馈控制
前轮反馈控制通过将前轮方向指向路径,使得前轮速度在路径法线的分量与车轮到路径的距离成正比。收敛速度是指数的。
横向误差满足:
可通过 δ 舵角控制。
在采用前轮控制的时候,后轮路径相应的变为
前轮反馈控制方法可以稳定的控制车辆在连续可微有变化曲率的路径上行使。也就是适用于我们见到的各种路段。缺点是在逆行不稳定,所以不适用于停车。
总结
上述基于运动学模型的车辆控制具有计算负荷低,易于应用的特点、中等行车速度时性能好。
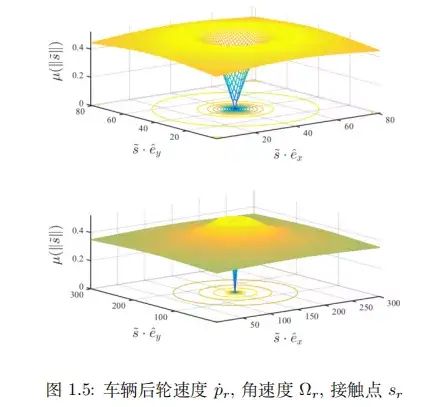
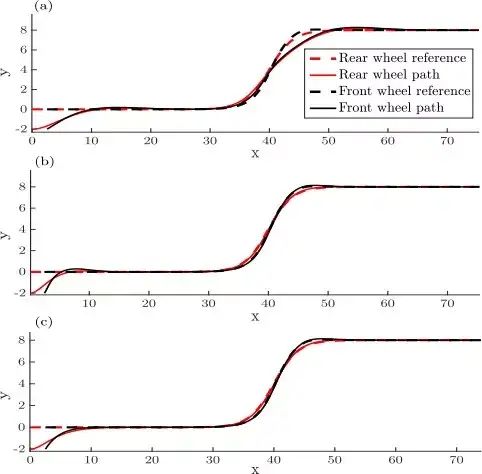
图 1.14: 前轮反馈控制
图 1.15: 前轮反馈控制参数
轨迹追踪方法适用于没有曲率的平直路段。在高曲率路段,可能会偏离参考路径。而基于前轮和后轮控制的方法则可以使车辆顺利通过。另外这三种方法都要求路径不可以自相交叉并且需要可微。
4.2 B. 动力学模型的轨迹跟踪
1). 基于 Lyapunov 的设计
在惯性坐标系中,由于轨迹带来的局部坐标误差:
车辆位姿变化的梯度
其中
2). 输出反馈线性化
高速运行的车辆,为保证连续运动需要约束舵角。增加的约束使得控制变得困难,将输出线性化是个不错的选择。
定义控制变量
输入的控制
4.3 C. 预测控制方法
对无人驾驶车辆应用运动规划控制需要在每秒内多次求解上述二次规划问题。这是一个巨大的计算负担,常常用内点法在多项式时间内求解二次规划问题。
近似线性模型:
然后控制规则变为:
在此基础上有很多变种预测模型:
1). 无约束 MPC 及动力学模型 不使用输入约束和状态约束及 CARIMA(受 控自回归积分滑动平均)。采用半闭环线性二次规划方法,计算负载小。
2). 路径跟踪控制器 路径追踪和近似驾驶模型,对质心积分的线性动态模 型。
3). 轨迹跟踪控制器 在冰雪环境下,采用轮胎模型,速度 21m/s 可以稳定 控制车辆。
4.4 线性参数变化控制
如 (1.32) 位姿的梯度可以表示为
05 结论
过去三十年无人驾驶技术飞速发展,计算和感知硬件也突飞猛进,算法研究和路网得建设也日新月异。整个无人驾驶系统每个环节得进步都会激起连锁反应,本文只是对各个方面做了简要的介绍,更多得细节和不断深入的研究等着大家的参与。