Java数据结构——树——AVL树
目录
一、简介
1.1 AVL树(自平衡二叉树)又和搜索(排序)树相比,有什么区别呢?
1.2 为什么我们需要树这种数据结构
1.3 为什么有了搜索树还要二叉平衡树
二、AVL树节点的自平衡处理
三、删除节点
四、代码实现
一、简介
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
AVL树本质上还是一棵二叉搜索树,它的特点是:
1.本身首先是一棵二叉搜索树。
2.带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。下图为AVL(自平衡)二叉树:
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树:
1.若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2.若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3.它的左、右子树也分别为二叉排序树。下图即为一个搜索(排序)树
我们一说到树,就会想到生活中的树,像这样:
大家有没有发现,除了没有树叶不能开花或者结果之外,是不是和我们计算机中的数据结构——树 一模一样
(觉得不像的朋友,可以把上图旋转180°观察)
而树的根,就相当于我们数据结构中树的根节点。
只不过计算机中的树成长方式和我们生活中的树的成长方式是相反的。
有常识的朋友都知道树是从下往上生长,但是计算机中的树则是从上往下生长。【类似扎根】在我们开始探讨树之前,必须要先理解树的一些基本术语:
节点:上面搜索树图片中的一个个圈圈叫节点。
根节点:最上层节点(也就是只有一个圈圈)就是这棵树的根节点。
子节点:节点下的左右两节点。
孙子节点:子节点下的子节点。
父节点:子字节之上的节点。
祖父节点:父节点的父节点。
兄弟节点:相邻的俩节点。
叔父节点:与父节点相邻的节点。
左子树:节点的左子节点下(包括)的所有节点。
右子树:节点的右子节点下(包括)的所有节点。
高度:节点的最大层数 (比如上面搜索树图片中节点的根节点高度为:4;其左子节点高度为:3 ;右子节点高度为:1)。
深度:高度的另一种说法
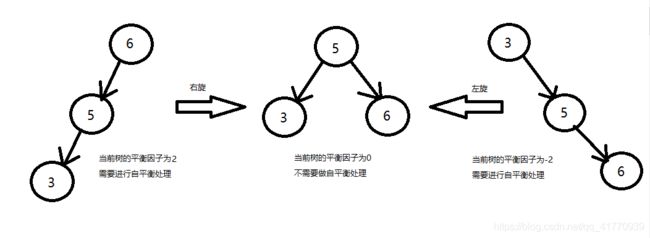
平衡因子:节点的左子树高度减去右子树高度的差。(AVL树的条件:差值必须在【1,-1】区间中,即左右子树高度比不能大于1)
左旋:逆时针旋转两个节点,让一个节点被其右子节点取代,而该节点成为右子节点的左子节点。
右旋:顺时针旋转两个节点,让一个节点被其左子节点取代,而该节点成为左子节点的右子节点。1.1 AVL树(自平衡二叉树)又和搜索(排序)树相比,有什么区别呢?
首先我们来对比这两张图有什么区别(排除颜色)
搜索二叉树 AVL树
为了让大家更直观,我用表格来展示
| 相同 | 不相同 | |
| 搜索树 | 节点数量,节点值 | 根节点的平衡因子为 2 |
| AVL树 | 节点数量,节点值 | 根节点的平衡因子为 0 |
判断搜索二叉树是否为平衡二叉树(AVL)的基准就是平衡因子
1.2 为什么我们需要树这种数据结构
为了能更方便快捷地处理互联网中的数据
1.3 为什么有了搜索树还要二叉平衡树
在本文上半部分中描述了搜索树的性质 —— 任意一节点的左子节点小于当前节点,右子节点大于当前节点
添加新节点判断节点大小从而找到该节点的位置
查找节点的时候,顺从该树的规则,查找的节点大于当前节点则找该节点的右子节点,反之查找当前节点的左子节点,直到找到该节点或者无节点时终止。二分查找算法就是用的这种思路。
但是如果加入的数据是按照大小规律来建立一棵搜索树时(比如从小到大),按照搜索树的性质,则会将搜索树退化为链表
比如:我们需要依次添加 1,2,3,4,5,6,7,8这几个数据
搜索树
如上图所示,退化为链表的搜索树,在查找数据的时候,时间复杂度为 O(n)
二叉树
如上图所示,二叉树在添加数据的同时会对数据进行自平衡操作,防止退化为链表,在查找数据的时候,时间复杂度为 O(logn)
至此,又引出了一个新问题:每添加一个节点就需要进行自平衡处理,在大数据处理过程中会占用大量资源,这其实并不可取。所以红黑树应时而生。不过本篇文章对红黑树不做过多赘述,有兴趣可以看看我的这篇博客。
二、AVL树节点的自平衡处理
自平衡讲解完毕
三、删除节点
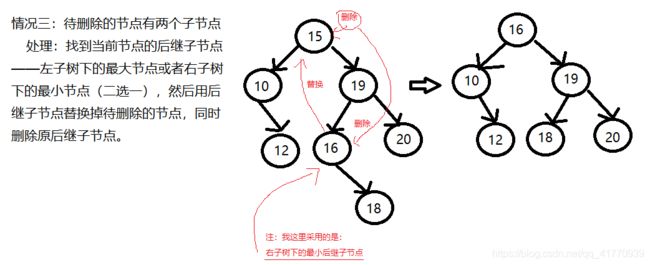
接下来我们进入比较难的一个环节——删除节点
删除的情况大致可以分为三种:
1.待删除的节点没有子节点
2.待删除的节点只有一个子节点
3.待删除的节点有两个子节点删除节点讲解完毕
四、代码实现
@Data
@AllArgsConstructor
@NoArgsConstructor
public class Node {
public int key;
public Node leftNode;
public Node rightNode;
public int height;
@Override
public String toString(){
JSONObject jsonObject = new JSONObject();
jsonObject.put("key",this.key);
jsonObject.put("leftNode",this.leftNode);
jsonObject.put("rightNode",this.rightNode);
jsonObject.put("height",this.height);
return jsonObject.toJSONString();
}
} /**
* 添加插入二叉树节点
* @param node 根节点
* @param key 当前添加或插入的节点
* @return
*/
public static Node insert(Node node,int key){
if (node == null){
return newNode(node,key);
}
// 判断当前添加的节点应该放在哪个位置,并返回其父节点
if (key < node.key){
node.leftNode = insert(node.leftNode,key);
}else if (key > node.key){
node.rightNode = insert(node.rightNode,key);
}else {
return node;
}
// 更新当前节点高度
node.height = max(height(node.leftNode),height(node.rightNode)) + 1;
// 获取当前节点的平衡因子
int balance = getBalance(node);
/* 当前节点的左子树高度与右子树高度比大于1 并且 当前添加的节点小于其祖父节点的左子节点
* 如:
* 3
* /
* 2 -> 2
* / / \
* 1 1 3
* LL型 需进行右旋操作
*/
if (balance > 1 && key < node.leftNode.key){
return ll_state(node);
}
/* 当前节点的左子树高度与右子树高度比小于-1 并且 当前添加的节点大于其祖父节点的右子节点
* 如:
* 1
* \
* 2 -> 2
* \ / \
* 3 1 3
* RR型 需进行左旋操作
*/
if (balance < -1 && key > node.rightNode.key){
return rr_state(node);
}
/* 当前节点的左子树高度与右子树高度比大于1 并且 当前添加的节点大于其祖父节点的左子节点
* 如:
* 3 3
* / /
* 1 -> 2 -> 2
* \ / / \
* 2 1 1 3
* LR型 需先进行左旋操作 再进行右旋操作
*/
if (balance > 1 && key > node.leftNode.key){
node.leftNode = rr_state(node.leftNode);
return ll_state(node);
}
/* 当前节点的左子树高度与右子树高度比小于-1 并且 当前添加的节点小于其祖父节点的右子节点
* 如:
* 1 1
* \ \
* 3 -> 2 -> 2
* / \ / \
* 2 3 1 3
* RL型 需先进行右旋操作 再进行左旋操作
*/
if (balance < -1 && key < node.rightNode.key){
node.rightNode = ll_state(node.rightNode);
return rr_state(node);
}
return node;
}
private static Node rr_state(Node node){
Node right = node.rightNode;
node.rightNode = right.leftNode;
right.leftNode = node;
node.height = max(height(node.leftNode),height(node.rightNode)) + 1;
right.height = max(height(node.leftNode),height(node.rightNode)) + 1;
return right;
}
private static Node ll_state(Node node){
Node left = node.leftNode;
node.leftNode = left.rightNode;
left.rightNode = node;
node.height = max(height(node.leftNode),height(node.rightNode)) + 1;
left.height = max(height(node.leftNode),height(node.rightNode)) + 1;
return left;
}
private static int getBalance(Node node){
return height(node.leftNode) - height(node.rightNode);
}
private static int max(int a,int b){
return a > b?a:b;
}
private static int height(Node node){
if (node == null)
return 0;
return node.height;
}
private static Node newNode(Node node, int key) {
return new Node(key,null,null,1);
}
// 删除节点
public static Node delete(Node root,int key){
if (root == null){
return root;
}
if (key < root.key){
root.leftNode = delete(root.leftNode,key);
}else if (key > root.key){
root.rightNode = delete(root.rightNode,key);
}else {
// 判断当前节点是否有子节点
if (root.leftNode == null || root.rightNode == null){
root = root.leftNode != null?root.leftNode:root.rightNode;
}else {
// 如果当前节点有左右子节点 则找到当前节点的后继子节点
Node temp = minNode(root.rightNode);
// 后继子节点替换掉当前节点
root.key = temp.key;
// 删除后继子节点
root.rightNode = delete(root.rightNode,temp.key);
}
}
if (root == null){
return root;
}
root.height = max(height(root.leftNode),height(root.rightNode)) + 1;
int balance = getBalance(root);
// LL
if (balance > 1 && getBalance(root.leftNode) >= 0){
return ll_state(root);
}
// RR
if (balance < -1 && getBalance(root.rightNode) <= 0){
return rr_state(root);
}
// LR
if (balance > 1 && getBalance(root.leftNode) < 0){
root.leftNode = rr_state(root.leftNode);
return ll_state(root);
}
// RL
if (balance < -1 && getBalance(root.rightNode) > 0){
root.rightNode = ll_state(root.rightNode);
return rr_state(root);
}
return root;
}
private static Node minNode(Node node) {
Node parent = node;
Node current = node;
while (current != null){
parent = current;
current = current.leftNode;
}
return parent;
} {\__/} {\__/}
( ·-·) (·-· )
/ >------------------------------------------------< \
| ☆ |
| ☆ |
| ★ |
| ☆ |
| ☆ |
| |
-------------------------------------