Java数据结构与算法（树）——平衡二叉树（AVL树）

一、定义

平衡二叉查找树（Balanced Binary Sort Tree，BBST）简称平衡二叉树，是一种高度平衡的二叉树，由苏联数学家 Adele - Veliki 和 Landis 在 1962 年提出，故又命名为 AVL 树。

平衡二叉树的性质：首先是一种二叉查找树，并且其中每个节点的左子树和右子树的高度相差至多等于 1。

平衡因子BF（Balance Factor）——将二叉树上节点的左子树高度减去右子树高度的值称为平衡因子。平衡二叉树上，所有节点的平衡因子只可能是 -1，0，1。

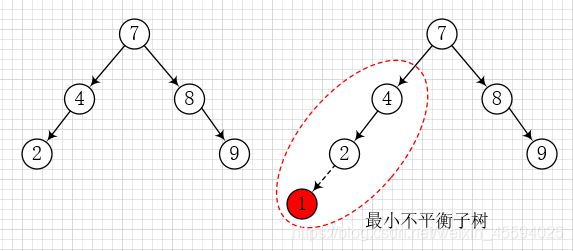
最小不平衡子树——距离插入节点最近的，且平衡因子的绝对值大于 1 的节点为根的子树。以下图为例，左图是一棵平衡二叉树，当插入节点 1 时，节点 4 的 BF = 2（左子树高度 - 右子树高度 = 2 - 0 = 2），则以节点 4 为根节点的子树即为最小不平衡子树。

二、不平衡情况及处理方法

构建平衡二叉树的基本思想就是在构建二叉搜索树的过程中，每当插入一个新节点时，先检查是否因插入而破坏了树的平衡性，若是，则在保持二叉搜索树特性的前提下，调整最小不平衡子树中各节点之间的链接关系，进行相应的旋转调整，使之成为新的平衡二叉树。

注意：
不平衡的情况其实千变万化，比如左边深度为一万，右边深度为 0。但是我们考虑的是，在平衡二叉树中修改一个节点以后引起的不平衡，所以，左右子树的差的绝对值只能为 2。

旋转的情况：

（1）单旋：
最小不平衡子树的根节点的 BF 与它的子树的 BF 符号相同时，需要一次旋转。最小不平衡子树的根节点的 BF 大于 1 时，右旋；小于 -1 时，左旋。

（2）双旋：
最小不平衡子树的根节点的 BF 与它的子树的 BF 符号相反时，需要两次旋转，即先对子树进行一次旋转后使得 BF 符号相同之后，再反向旋转一次完成平衡。

1、左左（右旋）

插入节点 1 时，原平衡二叉树失衡，右旋过程图示如下：

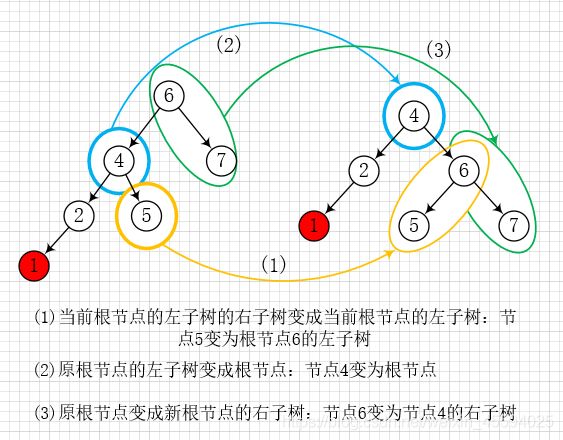
最小不平衡子树的根节点 6 的 BF = 2，左子树根节点 4 的 BF = 1，同号且大于 1，右旋。具体操作：

• 当前根节点的左子树的右子树变成当前根节点的左子树（因为它满足大于左子树且小于根节点的要求）；
• 原根节点的左子树变成新的根节点；
• 原根节点变成新根节点的右子树。

2、右右（左旋）

插入节点 8 时，原平衡二叉树失衡，左旋过程图示如下：

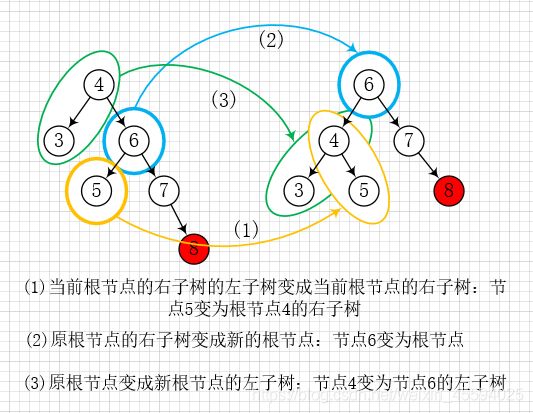
最小不平衡子树的根节点 4 的 BF = -2，右子树根节点 6 的 BF = -1，同号且小于 -1，左旋。具体操作：

• 当前根节点的右子树的左子树变成当前根节点的右子树；
• 原根节点的右子树变成新的根节点；
• 原根节点变成新根节点的左子树。

3、双旋

如下图，插入节点 8 时，最小不平衡子树的根节点 9 的 BF = 2，左子树根节点 6 的 BF = -1，反号，仅一次单旋不能解决问题。

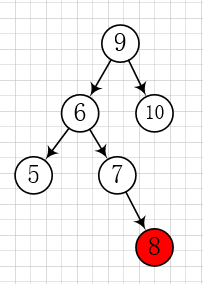
解决方法：

双旋：最小不平衡子树的左子树根节点 6 的 BF = -1，先左旋最小不平衡子树的左子树，再右旋最小不平衡子树。如下图所示：

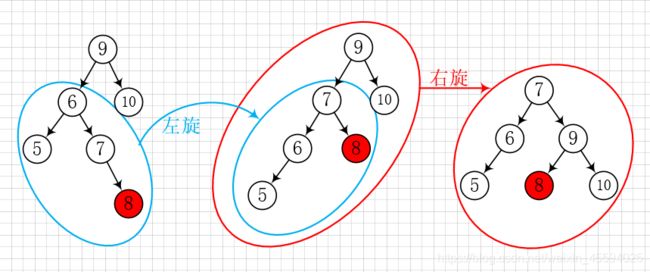
先右旋再左旋的情况类似。

三、代码实现

1、节点类抽象数据类型

public interface AVLNodeADT {
	void insert(AVLNode node);// 向平衡二叉树插入节点
	
	void preOrder();// 前序遍历
	
	void infixOrder();// 中序遍历
	
	void postOrder();// 后序遍历
	
	AVLNode find(int value);// 查找
	
	int getHeight();// 当前节点的高度
	
	int getLeftHeight();// 左子树的高度
	
	int getRightHeight();// 右子树的高度
	
	void leftRotate();// 左旋
	
	void rightRotate();// 右旋
}

2、节点类

public class AVLNode implements AVLNodeADT{
	private int value;
	private AVLNode left;
	private AVLNode right;
	
	public AVLNode(){}
	
	public AVLNode(int value){ this.value = value; }

	public int getValue() { return value; }

	public void setValue(int value) { this.value = value; }

	public AVLNode getLeft() { return left; }

	public void setLeft(AVLNode left) { this.left = left; }

	public AVLNode getRight() { return right; }

	public void setRight(AVLNode right) { this.right = right; }
	
	public String toString(){ return value + " "; }// 方便打印

	@Override
	// 插入:(1)插入节点(2)检查是否需要调整平衡
	public void insert(AVLNode node) {
		// (1)插入节点
		if(node == null)// 插入节点为空，直接返回
			return;
		if(node.value < this.value){// 插入节点值小于根节点的值，递归插入左子树 
			if(this.left == null)
				this.setLeft(node);
			else
				this.left.insert(node);
		}else if(node.value > this.value){// 插入节点值大于根节点的值，递归插入右子树 
			if(this.right == null)
				this.setRight(node);
			else
				this.right.insert(node);
		}else{// 相等说明节点已存在，不用再插入 
			return;
		}
		
		// (2)检查是否需要调整平衡
		int BF = this.getLeftHeight() - this.getRightHeight();// 平衡因子
		if(BF < -1){// 左旋
			// 若其右子树的BF > 1,需要双旋;否则只需单旋
			int rightBF = this.right.getLeftHeight() - this.right.getRightHeight();
			if(this.right != null && rightBF > 1){
				this.right.rightRotate();// 先对该节点的右子树进行右旋
			}
			this.leftRotate();// 再对当前节点进行左旋
		}else if(BF > 1){// 右旋
			// 若其左子树的BF < -1,需要双旋;否则只需单旋
			int leftBF = this.left.getLeftHeight() - this.left.getRightHeight();
			if(this.left != null && leftBF < -1){
				this.left.leftRotate();// 先对该节点的左子树进行左旋
			}
			this.rightRotate();// 再对当前节点进行右旋
		}else{// 平衡，不用调整
			return;
		}
	}

	@Override
	// 前序遍历
	public void preOrder() {
		System.out.print(this);
		if(this.getLeft() != null)
			this.left.preOrder();
		if(this.getRight() != null)
			this.right.preOrder();
	}

	@Override
	// 中序遍历
	public void infixOrder() {
		if(this.getLeft() != null)
			this.left.infixOrder();
		System.out.print(this);
		if(this.getRight() != null)
			this.right.infixOrder();
	}

	@Override
	// 后序遍历
	public void postOrder() {
		if(this.getLeft() != null)
			this.left.postOrder();
		if(this.getRight() != null)
			this.right.postOrder();
		System.out.print(this);
	}

	@Override
	// 查找
	public AVLNode find(int value) {
		if(value < this.value){// 搜索左子树
			if(this.left == null)
				return null;
			else
				return this.left.find(value);
		}else if(value > this.value){
			if(this.right == null)
				return null;
			else
				return this.right.find(value);
		}else{
			return this;
		}
	}

	@Override
	// 获取当前节点的高度(左子树高度和右子树高度较大值 + 1)
	public int getHeight() {
		// 666
		return Math.max(this.left == null ? 0 : this.left.getHeight(), 
				this.right== null ? 0 : this.right.getHeight()) + 1;
	}

	@Override
	// 获取左子树的高度
	public int getLeftHeight() {
		return this.left == null ? 0 : this.left.getHeight();
	}

	@Override
	// 获取右子树的高度
	public int getRightHeight() {
		return this.right== null ? 0 : this.right.getHeight();
	}

	@Override
	/*
	 * 左旋：
	 * 		(1)当前根节点的右子树的左子树变成当前根节点的右子树；
	 * 		(2)原根节点的右子树变成根节点；
	 * 		(3)原根节点变成新左子树。
	 */
	public void leftRotate() {
		// (1)当前根节点的右子树的左子树变成当前根节点的右子树；
		AVLNode node = new AVLNode(this.value);// 以当前根节点的值创建一个新节点，作为旋转之后根节点的左子树
		node.left = this.left;// 新节点的左子树还是其原来的左子树
		node.right = this.right.left;// 当前根节点的右子树的左子树变成当前根节点的右子树
		
		// (2)原根节点的右子树变成新根节点；
		this.value = this.right.value;
		this.right = this.right.right;// 新根节点的右子树还是其原来的右子树
		
		// (3)原根节点变成新根节点的左子树。
		this.left = node;
	}

	@Override
	/*
	 * 右旋：
	 * 		(1)当前根节点的左子树的右子树变成当前根节点的左子树；
	 * 		(2)原根节点的左子树变成新根节点，
	 * 		(3)原根节点变成新根节点的右子树。
	 */
	public void rightRotate() {
		// (1)当前根节点的左子树的右子树变成当前根节点的左子树;
		AVLNode node = new AVLNode(this.value);// 以当前根节点的值创建新节点，作为旋转之后根节点的右子树
		node.right = this.right;// 新节点的右子树还是其原来的右子树
		node.left = this.left.right;// 当前根节点的左子树的右子树变成当前根节点的左子树
		
		// (2)原根节点的左子树变成新根节点;
		this.value = this.left.value;
		this.left = this.left.left;// 新根节点的左子树还是其原来的左子树
				
		// (3)原根节点变成新根节点的右子树。
		this.right = node;
	}
}

3、平衡二叉树测试类

public class AVL {
	private AVLNode root;
	
	public AVL(){}
	
	public AVL(AVLNode root){ this.root = root; }
	
	// 插入
	public void insert(AVLNode node){
		if(root == null)
			root = node;
		else
			root.insert(node);
	}
	
	// 前序遍历
	public void preOrder(){
		if(root == null){
			System.out.println("The tree is empty!");
			return;
		}else{
			root.preOrder();
		}
		System.out.println();
	}
	
	// 中序遍历
	public void infixOrder(){
		if(root == null){
			System.out.println("The tree is empty!");
			return;
		}else{
			root.infixOrder();
		}
		System.out.println();
	}
	
	// 后序遍历
	public void postOrder(){
		if(root == null){
			System.out.println("The tree is empty!");
			return;
		}else{
			root.postOrder();
		}
		System.out.println();
	}
	
	// 查找节点
	public AVLNode find(int value){
		if(root == null){
			System.out.println("The tree is empty!");
			return null;
		}
		return root.find(value);
	}
	
	// 树的高度
	public int getHeight(){
		if(root == null)
			return 0;
		return root.getHeight();
	}
	
	public static void main(String[] args) {
		AVL tree = new AVL();
		tree.insert(new AVLNode(2));
		tree.insert(new AVLNode(1));
		tree.insert(new AVLNode(6));
		tree.insert(new AVLNode(4));
		tree.insert(new AVLNode(3));
		tree.insert(new AVLNode(5));
		tree.insert(new AVLNode(7));
		
		tree.infixOrder();
		tree.preOrder();
		tree.postOrder();
	}
}

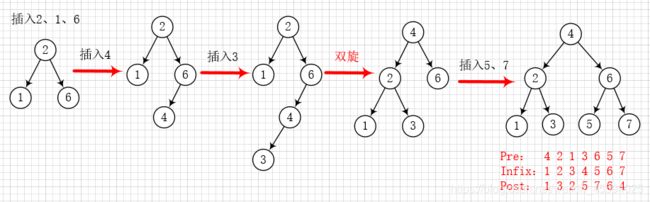
关于单旋（左旋，右旋）与双旋的处理都在添加节点后完成。添加一个节点，就对新的树进行判断是否需要"平衡"，所以添加节点的过程就是平衡二叉树的构建过程。上面的测试程序中，添加了 7 个数据，其构建平衡二叉树的过程图示如下：