基于Matlab的AR模型参数估计
基于Matlab的AR模型参数估计
AR(n)模型参数估计
已知测得的随机时间序列 y[n],对时间序列建立 y的 p 阶自回归 AR 模型。y[n]=a1 y[n-1]+a2 y[n-2]+…+ap y[n-p]+ε[n] 。最小二乘法进行适用性检验准则包括最终估计误差(FPE)准则、信息(AIC)准则、BIC 准则等,在此使用最小二乘法及以上三个准则对实例进行分析。

实例分析
用时间序列的最小二乘估计和 FPE、AIC 准则对 AR(n)模型进行参数估计,时间序列如图所示。

Matlab 程序设计
y=[162,175,162,156,174,157,154,177,159,171,166,162,171,183,163,152,165,175,167,170,170,167,171,164,163,170,164,162,167,166,153,173,158,174,170,167,157,178,163,163,158,154,149,178,160,164,160,171,153,178,160,155,169,156,161,166,169,172,169,161,163,171,171,163,171,165,159,161,157,161,175,151,164,180,162,153,182,158,166,178,169,161,174,155,165,167,165,165,169,165,162,151,171,169,157,173,163,161,168,152];
ybar=mean(y);z=y-ybar*ones(1,100);
% 对 1-15阶 AR 模 型 逐 个 参 数 估 计, 于 工 作 区 m/Report/Fit 查得 FPE,ALC,BIC 参数估计
y1=[];y2=[];y3=[];
for i=1:1:15
m1=ar(z,i,'fb');
y1=[y1 m1.Report.Fit.FPE];
y2=[y2 m2.Report.Fit.AIC];
y3=[y3 m2.Report.Fit.BIC];
end%采用循环分别赋值给y1y2y3
x=(1:1:15);
%以下为建立一个x轴三个y轴的代码
ha1 = axes('Position',[0.1 0.15 0.7 0.7],'ycolor','b');
h1 = line(x,y1,'parent',ha1);
set(gca,'XTick',0:1:16);
xlabel('AR 模型阶数') ;
ylabel('FPE') ;
ha2 = axes('Position',[0.1 0.15 0.7 0.7],'color','none','ycolor','r','xtick', [],'yaxislocation','right');h2 = line(x,y2,'color','r','parent',ha2);
ylabel('ALC');
ha3 = axes('Position',[0.1 0.15 0.7 0.7],'color','none','ycolor','none','xtick',[]); h3 = line(x,y3,'color','k','parent',ha3);
ha4 = axes('Position',[0.1 0.15 0.8 0.7],'color','none','ycolor','k','xtick',[],'yaxislocation','right');
h4 = line(x,y3,'color','none','parent',ha4);
ylabel('BIC')
title('对 AR(n)模型的参数估计 ');
结果分析
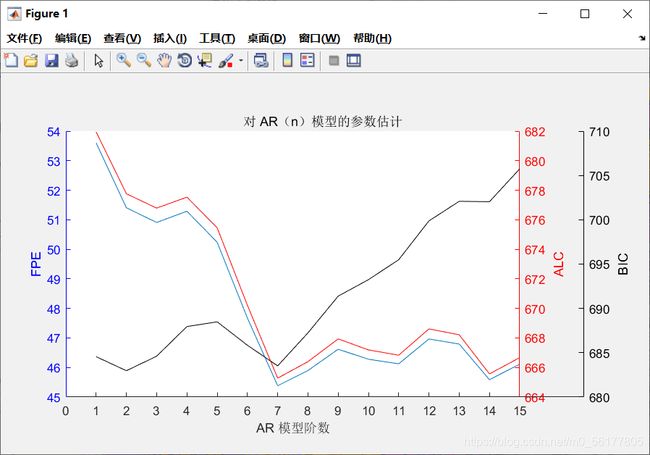
p=7 时,FPE , AIC,BIC 准则均取到该范围内的最小值。分析图像,由“当时间序列在两准则下各自取到最小值时即为适用模型”的理论得出:在 1-15阶 AR(p)的范围内,从精确性和模型尽量简约的原则出发,宜采用 AR(7)模型