CFAR原理详解及其matlab代码实现
引言：恒虚警检测算法在雷达目标识别中应用的比较多，最简单的有CA-CFAR啥啥的。其实该算法的应用很简单，只需要根据想要的虚警概率去计算
，再利用周围参考单元的值去估计待测单元的噪声功率，进而就能得到门限
（其中
为噪声功率）。
应用简单但是原理确实有些不好理解，故在此解释原理思路。
CFAR原理思路解释
CFAR其实可以归结为《信号检测与估计》中的内容，意为恒虚警检测，基于奈曼-皮尔逊准则。在雷达目标检测当中应用广泛。但是在使用其的时候，总是会思考为什么？为什么门限？为什么可以限定
(虚警概率)？为什么
可以由周围的参考单元去求得？为什么不直接求自身的单元进而求?
文献[1]中指出： 精确已知干扰功率是准确设定检测门限的前提条件，但是对一般雷达系统而言，干扰功率未知。为使雷达系统具有恒定的虚警概率，可以实时地从数据中估计实际干扰噪声功率电平，从而相应地调整雷达检测门限。恒虚警处理过程中所使用的方法基于两个主要假设:
1、待检测单元的杂波统计特性与临近单元所含杂波特性一致，临近单元所含杂波对于与潜在目标进行竞争的杂波具有代表性。
2、临近单元仅存在干扰噪声，不包含任何目标。
在上述主要假设下，可以从临近单元的数据中估计得到待检测单元的干扰杂波统计特性。待估计的干扰杂波统计特性由完成恒虚警概率门限检测所需要的量决定。
从上述讲述可以看出CFAR的思路：CFAR研究的是：待测单元未知、参考位置没有目标的情况。因为待测单元未知，故需要用周围参考单元的功率(没有目标，因此是噪声功率)去估计待测单元的噪声功率。而为了精准的设计出自适应门限，恰恰需要的就是噪声功率，只要得到了噪声功率之后，乘以(一般>>1)得到门限，之后将待测单元的值和这个门限比较若大于门限，也就意味着有目标。
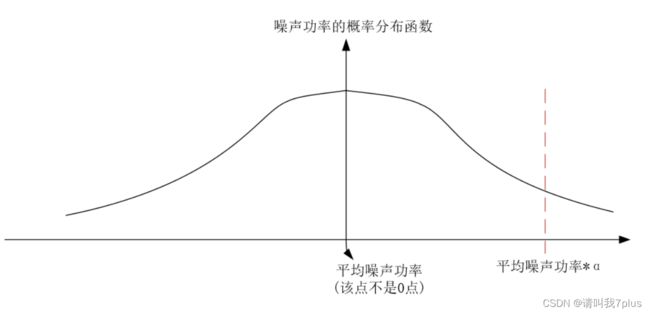
至于为什么要乘，和的取值与什么有关？关于为什么要乘这是因为噪声功率的分布是忽高忽低的，可能这一单元的功率高，下一单元你的功率就低。而前面估计出的是平均噪声功率，这样出现虚警的概率就会达到惊人的50%，很显然不是我们想要的。因此我们需要去乘以一个远远大于1的数去将这个概率降低，这里是有一个与的公式的，代码中有可以看一下，在这里不在写了。如下图所示乘以之后使得虚警概率也会大大降低(红线左边的区域)。
在这篇文章就不再填写公式只是探讨一下思路。以上大思路讲解完了，提一下具体的不同算法的操作。
1、CA-CFAR是利用周围参考单元的平均值去估计的待测单元的噪声功率。
2、还有其他的什么最小、最大是将周围参看单元排序之后取最大或最小的值去估计。
关于这几种算法有什么优缺点在此不多叙述，前者可以更稳定但是会有遮蔽效应，后者解决了遮蔽效应但...
一维CA-CFARmatlab演示及其代码[2]：
下面对一维CA-CFAR进行仿真：
结果不错。很有效的降低了噪声干扰。
代码：
%% 初始化
close all;
clc;
tarR = [10 20]; %目标距离
tarV = [-3 10]; %目标速度
c = 3*10^8;
f0 = 24.25*10^9;
T = 0.0002; %chirp Sweep Time
B = 400*10^6; %chirp bandwidth
L = 128; %slow-time dimension,num of chirps
N = 128; %fast-time dimension,num of samples
Npad = 1;
Lpad = 1;
%% 生成回波信号
S1 = zeros(L,N);
for l = 1:L
for n = 1:N
S1(l,n) = 500*exp(1i*2*pi*((2*B*(tarR(1)+tarV(1)*T*l)/(c*T)+(2*f0*tarV(1))/c)*T/N*n+((2*f0)*(tarR(1)+ tarV(1)*T*l ))/c));
end
end
S1 = awgn(S1,20);
S2 = zeros(L,N);
for l = 1:L
for n = 1:N
S2(l,n) = 500*exp(1i*2*pi*((2*B*(tarR(2)+tarV(2)*T*l)/(c*T)+(2*f0*tarV(2))/c)*T/N*n+((2*f0)*(tarR(2)+tarV(2)*T*l))/c));
end
end
S2 = awgn(S2,20);
sigReceive = S1+S2;
%% 距离维FFT
hanning1 = hanning(N,'periodic');
sigRWin = zeros(L,N);
for ii = 1:L
sigRWin(ii,:) = hanning1'.*sigReceive(ii,:);
end
sigRfft = zeros(L,N*Npad);
for ii = 1:L
sigRfft(ii,:) = fft(sigRWin(ii,:),N*Npad);
%第一行做fft
end
%% LFMCW雷达的信号序列。由于再次仅仅那只是模拟一维CA-CFAR故只分析其中一行
Rres = c/(2*B*Npad);
sigRfft1=sigRfft(1,:);
plot(Rres*(1:N*Npad),10*log(abs(sigRfft1))),title('Range Mesure')
xlabel('Range/m'),ylabel('Db');
hold on
%% 一维CA-CFAR
Pfa = 10^(-6);
Rres_rdm = c/(2*B);
Range_Dim = Rres_rdm*(1:N);
Range_Map = abs(sigRfft1);
referCell_num = 9;
proCell_num = 5;
proCell = zeros(proCell_num,1);
[r,c] = size(Range_Map);
CFAR_Map_num = 128 - (referCell_num-1);
CFAR_Map = zeros(CFAR_Map_num,1);
referCell = referCell_num;
alpha = referCell*(Pfa^(-1/referCell) - 1);
for i = 1:CFAR_Map_num
referWindow = Range_Map(i:i+referCell_num-1);
proCell = referWindow(1+(referCell_num - proCell_num)/2:referCell_num - (referCell_num - proCell_num)/2);
Beta = (sum(referWindow) - sum(proCell))/(referCell);
CFAR_Map(i) = alpha*Beta;
end
cha=referCell_num-proCell_num;
plot(Rres*(1+cha:N*Npad-cha),10*log(CFAR_Map));参考文献：
[1]严鑫. 毫米波雷达多目标检测与参数估计算法研究[D].东南大学,2017.
[2]FMCW雷达距离多普勒(RDM)处理方法中距离分辨率和速度分辨率的推导_GtJason_1998的博客-CSDN博客_多普勒分辨率
https://blog.csdn.net/qq_41248471/article/details/104276739