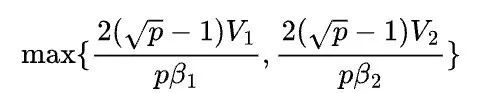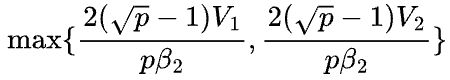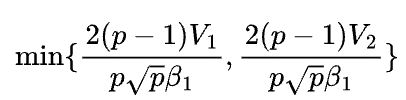手把手推导分布式矩阵乘的最优并行策略
作者｜郭冉、李一鹏、柳俊丞、袁进辉
常用深度学习框架的自动并行机制还不够完善，还需要用户根据经验来配置并行方式，这给开发者带来了不小的智力负担。因此，实现自动最优并行就成为一个有趣的课题。
矩阵乘是深度学习最常用的底层计算原语，譬如卷积算子，注意力机制都是通过矩阵乘来实现的，所以大规模神经网络的并行实现大多数时候也是在处理分布式矩阵乘。本文就以如何最优地实现分布式矩阵乘为例来展示自动并行的解决思路。
1
如何实现最优的分布式矩阵乘？
通过上一篇文章《手把手推导 Ring all-reduce 的数学性质》我们知道了常见集群通信操作的通信量和所需通信时间的数学性质，本文来探讨怎么使用这些性质来选择最优的并行矩阵乘策略。
在《如何超越数据并行和模型并行：从GShard 谈起》一文中，我们介绍了如何从一般的数据并行、模型并行提炼出最一般性的算子并行的抽象表示SBP。
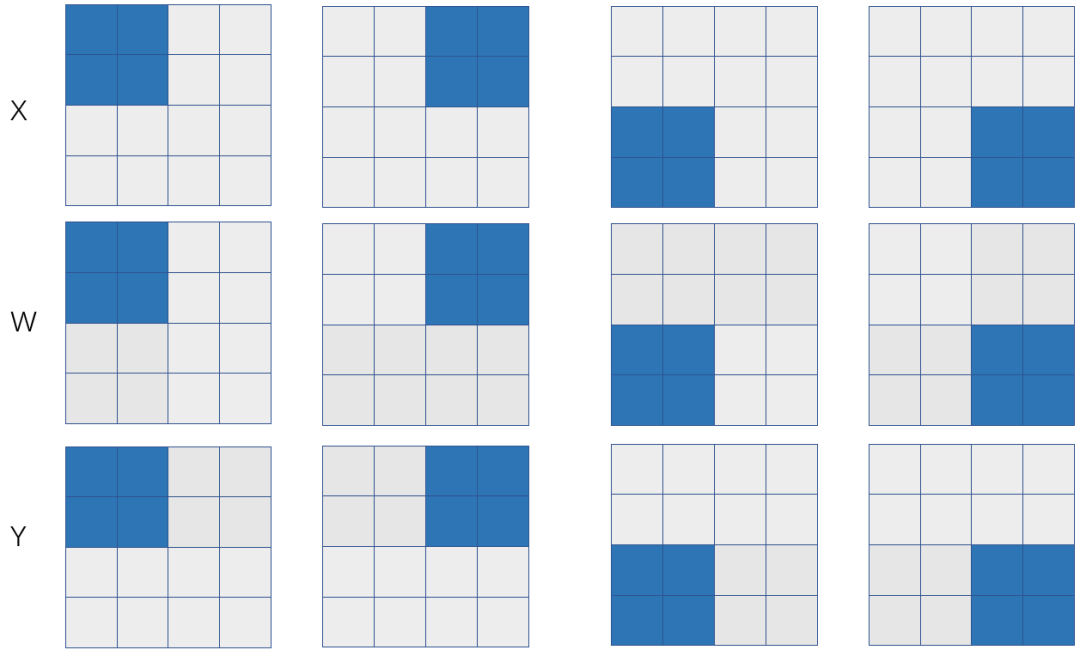
假设我们希望在4张显卡（2台服务器，每台服务器上有2张显卡）上完成一个矩阵乘X x W=Y，也就是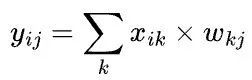
，其中X和W按照特定的SBP签名被摆放（place）到4张显卡上，那么将有多个方式实现分布式矩阵乘，它们在数学上等价，不过需要调用的集群通信操作不同，从而触发的通信代价也不同。
沿用《手把手推导 Ring all-reduce 的数学性质》里的符号，p表示设备数，V表示矩阵大小（
表示矩阵X的大小，
表示矩阵W的大小），
表示传输带宽。
2
数据并行还是模型并行？
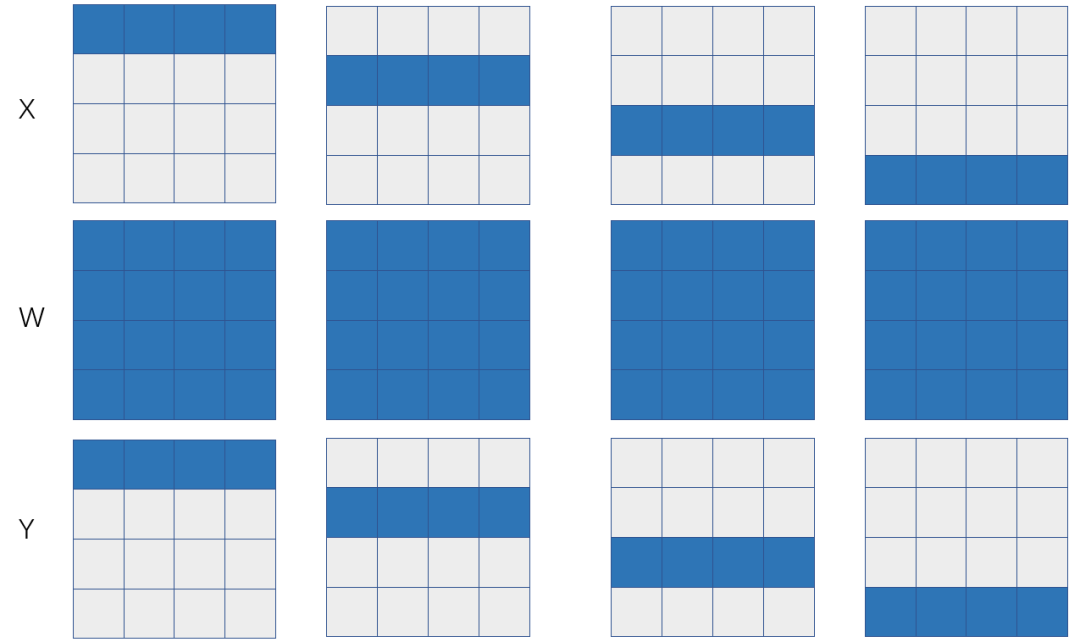
图 1：基于1D 矩阵乘的数据并行
如果X和W的SBP签名分别是S(0)和B，那么可以推导出来Y的SBP是S(0)，也就是左矩阵X是行划分，右矩阵W是在各个卡上是一模一样的拷贝（broadcast）。如果X表示特征数据 （feature map），W表示模型参数，那么这是一个典型的数据并行，下面我们分析一下数据并行的通信代价。
数据并行的反向需要执行集群通信操作all-reduce，如果采用环状算法，那么所有设备间的数据传输量是
，执行时间是
。
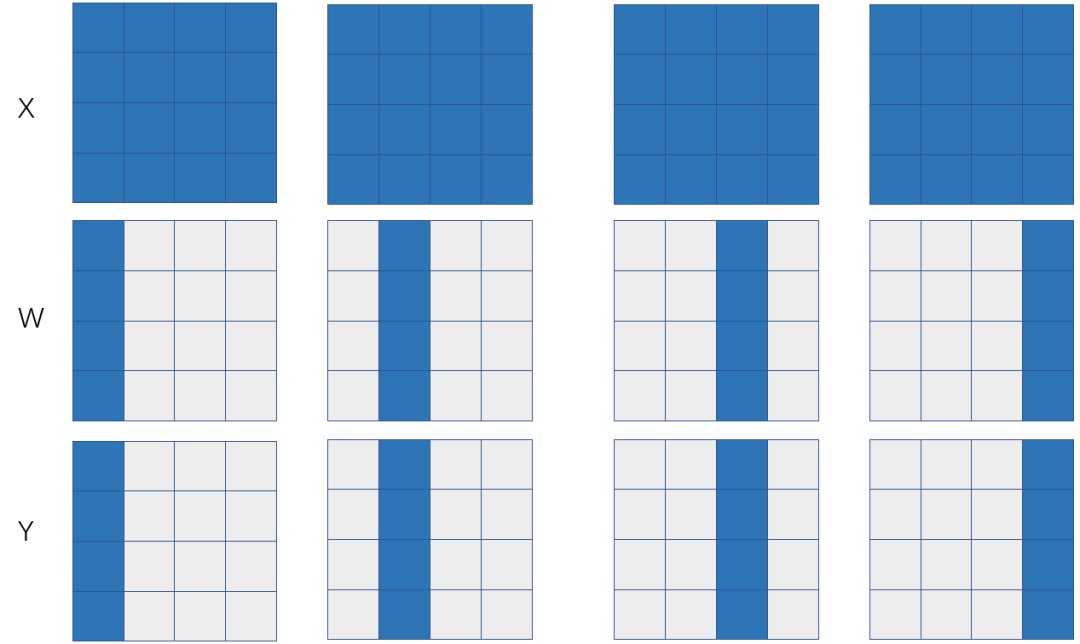
图 2：基于输出层神经元划分的模型并行
如果X和W的SBP签名分别是B和S(1)，那么可以推导出来Y的SBP是S(1)，也就是左矩阵X在各个卡上是一模一样的拷贝（broadcast），右矩阵W在各个卡上列划分。如果X表示特征数据 （feature map），W表示模型参数，那么这是一个典型的模型并行，下面我们分析一下这种模型并行的通信代价。
如果Y以S(1)的状态参与下游的计算，那么Y=X x W本身并不需要引入额外的通信。但假设Y需要被恢复成和X一样的状态（broadcast）参与下游计算，则前向计算时需要在S(1)签名的Y上调用all-gather操作，后向计算时需要在Y的反向error signal上调用reduce-scatter操作。那么前向和反向总的通信量是
，执行时间是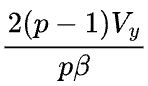
。
注意，矩阵乘引入的通信量不只是由当前算子决定的，还取决于它所处的上下文；这里的分析假设下游的算子需要Y保持和输入X一样的SBP签名，在这种情况下讨论不同并行方式的通信量。
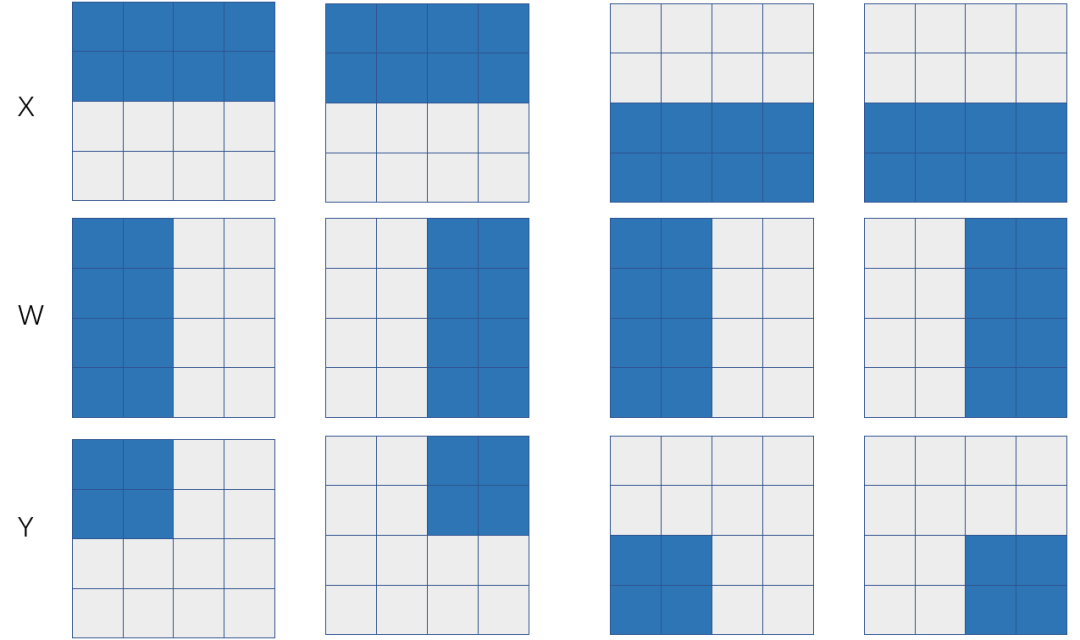
图 3：基于输入层神经元划分的模型并行
如果X和W的SBP签名分别是S(1)和S(0)，那么可以推导出来Y的SBP是P，也就是左矩阵X在各个卡上是列划分，右矩阵W在各个卡上行划分。如果X表示特征数据 （feature map），W表示模型参数，那么这也是一个模型并行的方式（只不过是对全连接层的输入神经元划分而来），下面我们分析一下这种模型并行的通信代价。
如果Y以与X相同的S(1)的状态参与下游的计算，则前向计算时需要在P签名的Y上调用 reduce-scatter 操作，后向计算时需要在Y的误差上调用all-gather操作。那么前向和反向总的通信量是
，执行时间是
。
根据以上的分析，数据并行的通信量是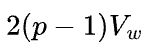
，模型并行的通信量是
，因此单就这一个矩阵乘而言，比较容易确定到底使用数据并行还是模型并行，也就是取决于
和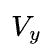
哪个大，如果
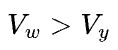，表示权重矩阵的容量大于输出特征数据的容量（譬如超大的全连接层），那么适合模型并行；如果
，表示权重矩阵的容量小于输出特征数据的容量（譬如卷积层），那么适合数据并行。
值得一提的是，在实践中，数据并行和模型并行还不单单由Vw和Vy哪个大来决定，数据并行中all-reduce通信比较容易被反向计算所掩盖，而模型并行的通信不容易被计算掩盖，因此即使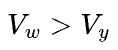
，理论上应该用模型并行，但当数据并行反向掩盖all-reduce的优势超过模型并行中通信量更小的优势时，使用数据并行是更优选择。这就是问题的复杂之处，最优的并行方式不仅仅是一个代价函数决定的，还和系统具体实现密切相关。
3
高维并行（矩阵乘）是怎么回事？
在英伟达为大规模预训练模型开发的Megatron-LM里，矩阵乘使用了2D并行，譬如同一个算子在机器间使用了数据并行，机器内部使用了模型并行。有一篇论文也提出2D并行来实现矩阵乘An Efficient 2D Method for Training Super-Large Deep Learning Models（https://arxiv.org/pdf/2104.05343.pdf）。
2D并行是怎么回事？真的会带来好处吗？为什么呢？我们还没有发现已有文献对这个问题从理论上讨论清楚，希望这篇博客能彻底搞清楚这些问题。
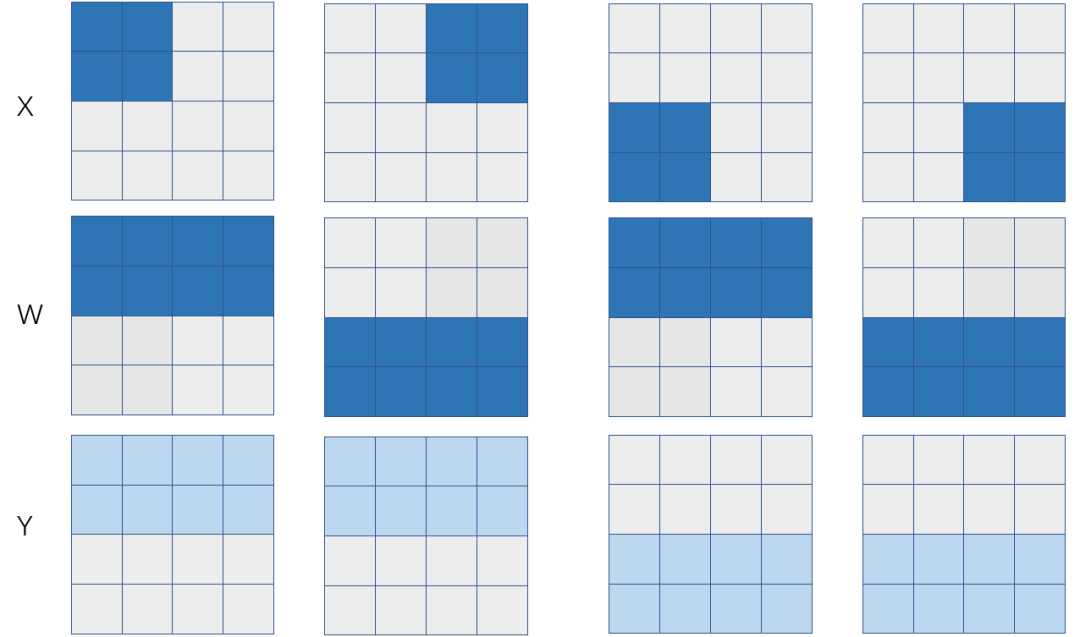
图 4：2D 并行
假设我们有2台机器，每台机器2个设备，X在机器间是S(0)，在机器内部是B，而W在机器间是B，在机器内部是S(1)，计算结果在机器间是S(0),机器内部是S(1)。
这个例子里，机器间是数据并行，机器内部是模型并行。
把Y从{S(0),S(1)}转换成和X一样的{S(0),B}，那么前向计算需要每台机器内部执行all-gather，反向需要在每台机器内部执行reduce-scatter，其传输量是
。同时，机器之间是数据并行，反向计算需要在第1台机器的第1张卡和第2台机器的第1张卡之间，以及第1台机器的第2张卡和第2台机的第2张卡之间分别调用all-reduce，传输量是
，总的传输量是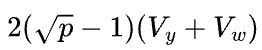
。
以2D的all-gather为例，我们再细致地解释一下上述的传输量是怎么推导出来的。
假设一共
台机器，每台机器上有
个设备，每台机器内部需要在
个设备之间完成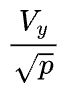
大小的矩阵，所以每台机器内部的传输量是
，一共
台机器，因此前向all-gather 传输量是
。
图 5：2D 矩阵乘
2台机器，每台机器2个设备，X在机器间是S(0)，在机器内部是S(1)，而W在机器间是B，在机器内部是S(0)，计算结果在机器间是S(0)，机器内部是P。
机器间是数据并行，机器内部是模型并行。
把Y从{S(0),P}转换成和X一样的{S(0),S(1)}，那么前向计算需要每台机器内部执行reduce-scatter，反向需要在每台机器内部执行all-gather，其传输量是
。同时，机器之间是数据并行，反向计算需要在第1台机器的第1张卡和第2台机器的第1张卡之间，以及第1台机器的第2张卡和第2台机器的第2张卡之间分别调用all-reduce，传输量是
，总的传输量是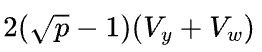
。
图 6：2D 矩阵乘
图6展示了经典的2D SUMMA 算法的实现。直接按照图6所示的数据分布是无法直接执行矩阵乘的，X和W在机器内部都需要执行all-gather计算，变成图4所示的数据分布才可以，相应的反向计算需要在机器内部执行reduce-scatter，总的通信量是
。
4
高维矩阵乘有什么好处？
以图4所示的2D矩阵乘为例，我们来讨论高维矩阵乘相对于1D矩阵乘带来了什么好处。
首先假设
，那么1D矩阵乘的通信量是2(p-1)V，而2D矩阵乘的通信量是
，基本上可以认为，当p>4，2D矩阵乘通信量就小于1D矩阵乘的通信量了。
可以推测，如果是3D矩阵乘，那么通信量和
成正比。高维矩阵乘的本质是减小了每一个集群通信操作的”宽度“，我们曾在上一篇博客《手把手推导 Ring all-reduce 的数学性质》推导出，集群通信的通信量和通信宽度成正比。
5
高维矩阵乘会降低通信时间吗？
细心的朋友可能注意到了，我们在讨论1D矩阵乘的通信代价时，总是同时讨论通信量和通信时间，但是在讨论2D矩阵乘的通信代价时，却只讨论了通信量，没有讨论通信时间。刚才我们也讨论了，高维矩阵乘会降低通信量，那么高维矩阵乘的通信时间也会降低吗？
实际上不会。结论有点违反直觉，为什么呢？原因是：通信量变成原来的
，但每个设备同时参与多组集群通信，每组集群通信可使用的带宽也变成原来的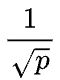
。下面看一个具体的例子。
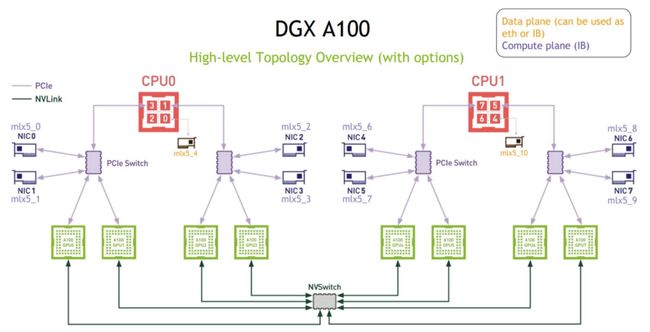
图 7：DGX-A100 通信拓扑
图7展示了DGX-A100机器的通信拓扑，假设一共有4台机器，每台机器有4个 GPU，每台机器有4张网卡，因此机器之间的带宽是每张网卡带宽的4倍。
图 8：1D 并行的环状通信拓扑
在1D并行中，假设所有GPU构成图8所示的一个大环。机器间通信带宽为
（注意：下文的公式和上文公式带宽差一个
系数，来源于此），其中
表示IB网卡带宽，在DGX A100拓扑中，机器间IB带宽通常小于机器内GPU设备间通信带宽，因此此处整体通信受限于机器间带宽，通信时间为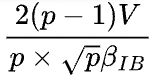
（注意：分母需要乘以设备总数p）。
图 9：2D 并行的环状通信拓扑
在2D并行中，以SUMMA矩阵乘法为例，每行的4个GPU设备构成一个环，即[machine 0 : gpu 0， machine 1 : gpu0， machine 2 : gpu 0， machine 3 : gpu0]、[machine 0 : gpu 1， machine 1 : gpu1， machine 2 : gpu 1， machine 3 : gpu1]组成一个环等，每列的4个GPU设备也构成一个环。
前向计算时，每个环上都要同时执行 all-gather 操作，跨机器的每个集群通信操作都会占用1/
的网络带宽，也就是
，机器内部的每个集群通信带宽不是瓶颈所在，因此不影响最终结果。通信时间不难推导出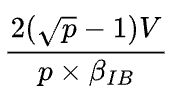
（这里除以p得到的是每个设备的通信量），和1D并行的通信时间
是同一个数量级。
至此可以得出：2D矩阵乘减小了集群通信的宽度，因此降低了所需要的通信量，但不会降低通信时间。
甚至，在特定的情况下，1D矩阵乘的通信时间要小于2D矩阵乘，这又是为什么？
2D矩阵乘的通信时间是
其中区别了不同的矩阵和不同环的传输带宽。假设
（机器间带宽小于机器内部带宽），那么2D矩阵乘的通信时间至少是
1D矩阵乘的通信时间是在数据并行和模型并行中选择更优的那一个：
当
和
相差比较悬殊时，不妨假设
<
，那么2D并行通信时间的下界是
，而1D并行的通信时间是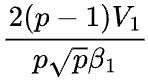
，不难得到，当
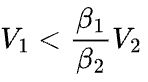时，1D并行的通信时间一定小于2D并行的通信时间。
因此，2D并行在降低通信量（或带宽需求）上有优势，1D并行在降低通信时间上有优势。
一般来说，一个神经网络中同时存在很多类似矩阵乘的算子，算子层次的并行都需要引入通信需求。通信带宽非常充裕，那么就可以放心的使用1D并行，这样确保通信时间是最小的；如果通信带宽是瓶颈，那么每一个算子都应该尽可能降低通信量的需求，节省带宽，这样才能让总体的通信时间最小。
2D并行的带宽需求降低了，但通信时间没有变化，原因是什么？直观的理解是，在2D并行中一定有一部分带宽是被闲置了。想象一下，一个大环被切成几段，形成几个小环，小环和小环之间的带宽是不需要用的。
6
结语
如果你在GPU上实现过单卡矩阵乘法，那可能对上面2D矩阵乘的示意图很熟悉，没错，在单卡实现矩阵乘时，关键也在于尽可能减小global memory和shared memory之间的数据搬运。
因此，那里也需要做类似于分布式矩阵乘的通信代价分析，分布式是宏观层次的数据搬运，单卡是微观层次的数据搬运，二者在原理上非常相似。实际上，已有文献对分布式矩阵乘的通信代价的理论分析已经非常成熟，本文讨论的2D阵乘或3D矩阵乘的实现方式都已实现了各自拓扑下通信代价的理论下界。
本文只讨论了一个算子并行时的最优策略，其实每个算子的最优策略也和它所处的上下文相关，一个算子不仅仅要考虑那个并行策略对自身是不是有利，还要考虑它的计算结果对周围的算子是不是有利。
因此，给定一个神经网络，它的最优并行策略是一个组合优化问题，如果这个神经网络是链状（chain-structure）的，那么可以证明，使用动态规划算法就可以在多项式时间内求出全局最优解，当神经网络的结构不是链状时，就无法使用动态规划，就需要一系列手段尽可能降低搜索空间的规模。
auto-placement和auto-parallelism是业界广泛关注的一个热点问题。很多研究工作直接就把问题形式化成一个组合优化的问题，但比较少讨论分布式深度学习自身的数学规律。
OneFlow团队在研究过程中发现，如果能对问题本身的数学性质做深入的理论分析，充分利用这些理论性质，auto-placement和auto-parallelism的求解可以出乎意料的简单。
迄今为止，我们应该对数据并行和模型并行讨论得很深入了，未来，我们会对流水并行的理论性质展开讨论。
正如本文在讨论1D并行和2D并行实现时所画的各种示意图所示，不同的数据切分方式带来不同的并行方式，也带有不同的通信代价。有些切分方式并不直观，怎么才能从理论上保证一种切分方式是正确的？怎么才能穷尽所有理论上正确的切分方式？
OneFlow SBP提供了一种很强大的数学抽象，不仅可以用来分析1D矩阵乘，还可以很方便地分析2D矩阵乘，大大简化了分析这些复杂问题的难度。强烈推荐做这方面工作的小伙伴儿都来用这套工具。
如果想更具体了解SBP如何在分布式模型训练里发挥威力，可以参照 OneFlow 发布的LiBai (https://github.com/Oneflow-Inc/libai) ，仅仅1万行核心代码就实现了NVIDIA Megatron-LM和Microsoft DeepSpeed需要五六倍代码量才能实现的功能。
其他人都在看
深度学习六十年简史
25倍性能加速，OneFlow“超速”了
天才制造者：独行侠、科技巨头和AI
拯救工程师，远程开发C++的四大秘笈
手把手推导Ring All-reduce的数学性质
解读Pathways（二）：向前一步是OneFlow
OneFlow v0.7.0发布：全新分布式接口，LiBai、Serving等一应俱全
点击“阅读原文”，欢迎下载体验OneFlow v0.7.0
