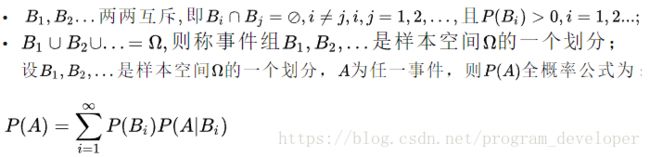【机器学习之 朴素贝叶斯】6.1 贝叶斯分类器
文章目录
- 6. 朴素贝叶斯
-
- 6.0 贝叶斯决策论
-
- 6.0.1 简介
- 6.0.2 贝叶斯解决的问题-逆概
- 6.1.3 先验概率和后验概率
-
- 1) 条件概率
- 2) 先验概率
- 3) 后验概率
- 4) 例子介绍
- 6.0.4 贝叶斯定理
-
- 1) 公式
- 2) 出现原因(逆概问题)
- 6.0.5 例子
-
- 2) 例一
- 3) 例二
- 4) 例三
- 6.0.6 全概率
- 6.1 贝叶斯分类器
-
- 6.1.1 贝叶斯判定准则
-
- 1) 期望损失(条件风险)R(x)
- 2) 最小条件风险的类别标记h(x)
- 3) 最小化分类错误率的贝叶斯最优分类器
- 4) 问题描述
- 5) 常见问题
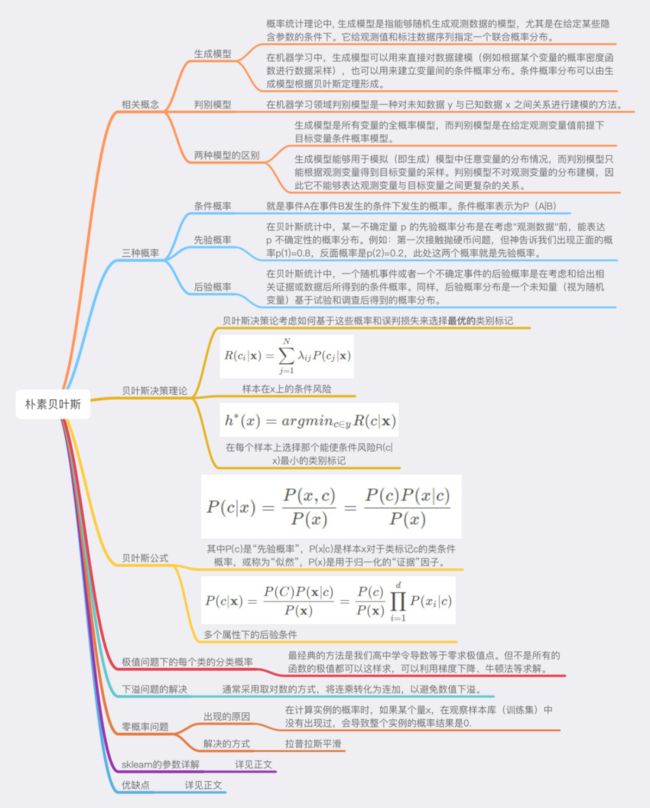
6. 朴素贝叶斯
文章链接 https://gitee.com/fakerlove/machine-learning
视频讲解:https://www.bilibili.com/video/BV14S4y1q7Ae
图是别人的,copy过来的,
6.0 贝叶斯决策论
学习贝叶斯的话,需要概率论的知识。不然完全听不懂
6.0.1 简介
贝叶斯分类器是一类分类算法的总称,贝叶斯定理是这类算法的核心,因此统称为贝叶斯分类。
贝叶斯决策论通过相关概率已知的情况下利用误判损失来选择最优的类别分类。
朴素贝叶斯(Naive Bayesian algorithm)是有监督学习的一种分类算法,它基于“贝叶斯定理”实现,该原理的提出人是英国著名数学家托马斯·贝叶斯。贝叶斯定理是基于概率论和统计学的相关知识实现的,因此在正式学习“朴素贝叶斯算法”前,我们有必要先认识“贝叶斯定理”。
6.0.2 贝叶斯解决的问题-逆概
介绍一下,啥叫正向概率,啥叫逆向概率?才能理解下面的 相关概念
正向概率:假设袋子里面有 N N N个白球, M M M个黑球,你伸手进去摸一把,摸出黑球的概率是多大??逆向概率:如果我们事先不知道袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,观察这些取出来的球的颜色之后,那么我们可以就此对袋子里面的黑白球的比例作出什么样子的推测??
下面有个图,方便理解
假设学校里面的人的总数是 U U U个
穿长裤的男生 U × P ( B o y ) × P ( P a n t s ∣ B o y ) U\times P(Boy)\times P(Pants|Boy) U×P(Boy)×P(Pants∣Boy)
- P ( B o y ) P(Boy) P(Boy)是男生的概率=60%
- P ( P a n t s ∣ B o y ) P(Pants|Boy) P(Pants∣Boy)是条件概率,即在 B o y Boy Boy这个条件下穿长裤的概率是多大,这里是100%,因为所有男生都穿长裤
穿长裤的女生: U × P ( G i r l ) × P ( P a n t s ∣ G i r l ) U\times P(Girl)\times P(Pants|Girl) U×P(Girl)×P(Pants∣Girl)
求解:穿长裤的人里面有多少女生??
- 穿长裤总数 C o u n t s = U × P ( B o y ) × P ( P a n t s ∣ B o y ) + U × P ( G i r l ) × P ( P a n t s ∣ G i r l ) Counts=U\times P(Boy)\times P(Pants|Boy)+U\times P(Girl)\times P(Pants|Girl) Counts=U×P(Boy)×P(Pants∣Boy)+U×P(Girl)×P(Pants∣Girl)
- P ( G i r l ∣ P a n t s ) = U × P ( G i r l ) × P ( P a n t s ∣ G i r l ) C o u n t s P(Girl|Pants)=\frac{U\times P(Girl)\times P(Pants|Girl)}{Counts} P(Girl∣Pants)=CountsU×P(Girl)×P(Pants∣Girl)
6.1.3 先验概率和后验概率
首先得了解什么叫做 先验概率,后验概率,全概率公式等相关概念
1) 条件概率
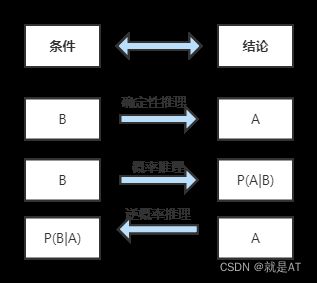
条件概率是“贝叶斯公式”的关键所在,那么如何理解条件概率呢?其实我们可以从“相关性”这一词语出发。举一个简单的例子,比如小明和小红是同班同学,他们各自准时回家的概率是 P(小明回家) = 1/2 和 P(小红回家) =1/2,但是假如小明和小红是好朋友,每天都会一起回家,那么 P(小红回家|小明回家) = 1 (理想状态下)。
上述示例就是条件概率的应用,小红和小明之间产生了某种关联性,本来俩个相互独立的事件,变得不再独立。但是还有一种情况,比如小亮每天准时到家 P(小亮回家) =1/2,但是小亮喜欢独来独往,如果问 P(小亮回家|小红回家) 的概率是多少呢?你会发现这两者之间不存在“相关性”,小红是否到家,不会影响小亮的概率结果,因此小亮准时到家的概率仍然是 1/2。
贝叶斯公式的核心是“条件概率”,譬如 P(B|A),就表示当 A 发生时,B 发生的概率,如果
P(B|A)的值越大,说明一旦发生了 A,B 就越可能发生,两者可能存在较高的相关性。
2) 先验概率
先验概率 是指在事件未发生时,估计该事件发生的概率。
比如投掷一枚匀质硬币,“字”朝上的概率。
3) 后验概率
后验概率 是指基于某个发生的条件事件,估计某个事件的概率,它是一个条件概率。
P(A|B)=P(类别|特征),我们根据看到的特征,判断类别。这里讲的一个就是逆概问题
我们知道每一个事物都有自己的特征,比如前面所说的轿车、货车、客车,它们都有着各自不同的特征,距离过远的时候,我们无法用肉眼分辨,而当距离达到一定范围内就可以根据各自的特征再次做出概率预判,这就是后验概率。
比如轿车的速度相比于另外两者更快可以记做 P(轿车|速度快) = 55%,而客车体型可能更大,可以记做 P(客车|体型大) = 35%。
如果用条件概率来表述 P(体型大|客车)=35%,这种通过“车辆类别”推算出“类别特征”发生的的概率的方法叫作“似然度”。这里的似然就是“可能性”的意思。
4) 例子介绍
下面例子,看不懂,就看上面的学生的例子。下面还有几个例子
玩英雄联盟占到中国总人口的60%,不玩英雄联盟的人数占到40%:
为了便于数学叙述,这里我们用变量X来表示取值情况,根据概率的定义以及加法原则,我们可以写出如下表达式:
P(X=玩lol)=0.6;P(X=不玩lol)=0.4,这个概率是统计得到的,或者你自身依据经验给出的一个概率值,我们称其为先验概率(prior probability);
另外玩lol中80%是男性,20%是小姐姐,不玩lol中20%是男性,80%是小姐姐,这里我用离散变量Y表示性别取值,同时写出相应的条件概率分布:
P(Y=男性|X=玩lol)=0.8,P(Y=小姐姐|X=玩lol)=0.2
P(Y=男性|X=不玩lol)=0.2,P(Y=小姐姐|X=不玩lol)=0.8
那么我想问在已知玩家为男性的情况下,他是lol玩家的概率是多少:
依据贝叶斯准则可得:
P ( X = l o l ∣ Y = m a n ) = P ( Y = m a n ∣ X = l o l ) × P ( X = l o l ) P ( Y = m a n ∣ X = l o l ) × P ( X = l o l ) + P ( Y = m a n ∣ X = n o t l o l ) × P ( X = n o t l o l ) P(X=lol|Y=man)=\frac{P(Y=man|X=lol)\times P(X=lol)}{P(Y=man|X=lol)\times P(X=lol)+P(Y=man|X=notlol)\times P(X=notlol)} P(X=lol∣Y=man)=P(Y=man∣X=lol)×P(X=lol)+P(Y=man∣X=notlol)×P(X=notlol)P(Y=man∣X=lol)×P(X=lol)
最后算出的P(X=玩lol|Y=男性)称之为X的后验概率,即它获得是在观察到事件Y发生后得到的
6.0.4 贝叶斯定理
上面做了这么多铺垫,下面就讲一下这一章最核心的朴素贝叶斯定理,
说白了就是一个公式。计算后验概率的
1) 公式
简单公式
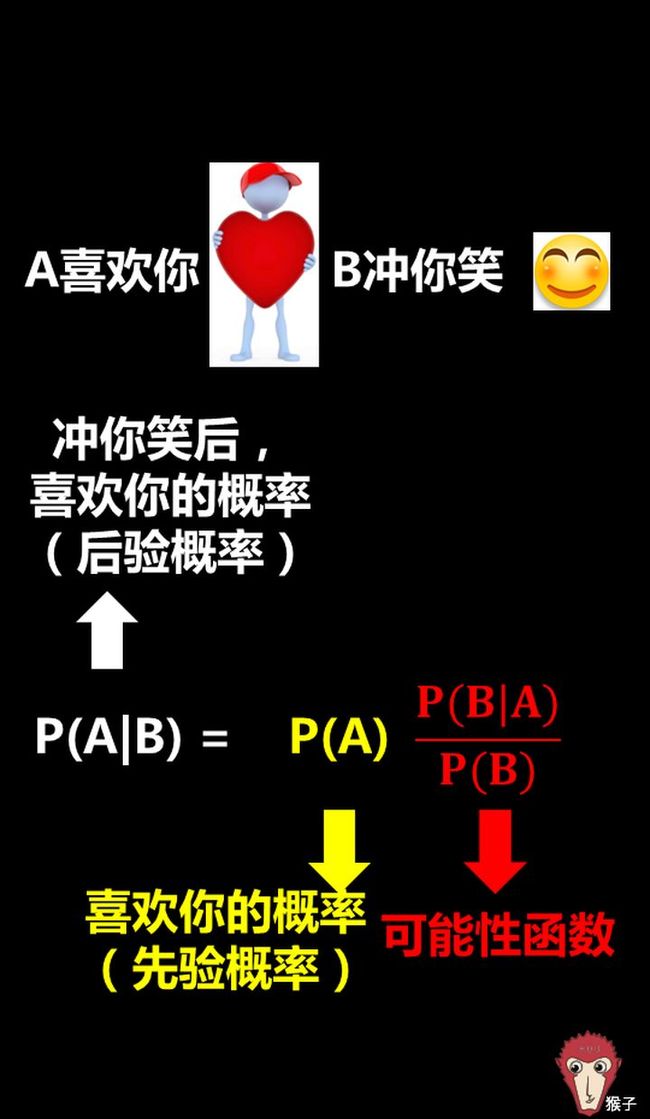
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) P(A|B)=P(A)\frac{P(B|A)}{P(B)} P(A∣B)=P(A)P(B)P(B∣A)
首先我们要了解上述公式中符号的意义:
- P(A) 这是概率中最基本的符号,表示 A 出现的概率。比如在投掷骰子时,P(2) 指的是骰子出现数字“2”的概率,这个概率是 六分之一。
- P(B|A) 是条件概率的符号,表示事件 A 发生的条件下,事件 B 发生的概率,条件概率是“贝叶斯公式”的关键所在,它也被称为“似然度”。
- P(A|B) 是条件概率的符号,表示事件 B 发生的条件下,事件 A 发生的概率,这个计算结果也被称为“
后验概率”。 - P ( B ∣ A ) P ( B ) \frac{P(B|A)}{P(B)} P(B)P(B∣A)可能性函数
通用公式
P ( A i ∣ B ) = P ( A i ) P ( B ∣ A i ) ∑ j = 1 n P ( A j ) P ( B ∣ A j ) P(A_i|B)=P(A_i)\frac{P(B|A_i)}{\sum_{j=1}^nP(A_j)P(B|A_j)} P(Ai∣B)=P(Ai)∑j=1nP(Aj)P(B∣Aj)P(B∣Ai)
- P ( B i ∣ A ) P(B_i|A) P(Bi∣A): 后验概率
- P ( A ∣ B j ) P(A|B_j) P(A∣Bj):类条件概率
- P ( B j ) P(B_j) P(Bj): 先验概率
- P ( A ) P(A) P(A):全概率
如果参照上面的逆概的思路,可以写成下面的东西,更加的容易懂
对于每个特征 x x x,我们想要知道样本在这个特性x下属于哪个类别,即求后验概率 P ( c ∣ x ) P(c|x) P(c∣x)最大的类标记。
这样基于贝叶斯公式,可以得到:
2) 出现原因(逆概问题)
如果能掌握事情的全部信息,当然能够计算出一个客观概率(古典概率)
但是生活中的大多数决策面临的信息都是不全的,我们手中只有有限的信息,既然无法得到全部信息,我们就在信息有限的情况下,尽可能做出一个好的预测。
也就是在主观判断的基础上先估一个值(先验概率),然后根据观察的新的信息不断修正(可能性函数)
6.0.5 例子
2) 例一
你认识一个女孩,突然你知道她喜欢去夜店蹦迪。
假如女孩中十个有一个就是渣女,那么女孩中渣女的比例占全体的0.1,正经女孩的比例占全体的0.9;
| 0.1 | 0.9 |
|---|---|
| 渣女 | 正经女孩 |
找出正经女孩和渣女蹦迪的概率,我们没有相关数据,但是不要紧,我们可以设定先验概率;
众所周知,蹦迪的女孩经常穿着暴露,经常和陌生男人“不小心”会有敏感部位的肢体接触,
可以断定,是渣女的概率远远超过正经女孩;我们可以预设:
| 类别 | 爱蹦迪 | 不爱蹦迪 |
|---|---|---|
| 正经女孩 | 0.05 | 0.95 |
| 渣女 | 0.5 | 0.5 |
一共存在四种可能性:渣女爱蹦迪、渣女不爱蹦迪、正经女孩爱蹦迪、正经女孩不爱蹦迪;它们的面积分别为:0.05、0.05、 0.045、 0.855;
| 0.1 | 0.9 |
|---|---|
| 渣女爱蹦迪0.05=0.1*0.5 | 正经女孩爱蹦迪0.045=0.05*0.9 |
| 渣女不爱蹦迪0.05=0.1*0.5 | 正经女孩不爱蹦迪0.855=0.95*0.9 |
作为一个男人,现在你面临的情况是:这个女孩爱蹦迪。这意味着,你观察到了该女孩的某一种行为。这条信息的内容是:“该女孩不蹦迪”的可能性消失了。上面提到,女孩分为“渣女”和“正经女孩”两类,女孩的行为分为“爱蹦迪”和“不爱蹦迪”两类,可能的世界一共分为四种。
在现实世界中,因为已经观测到“爱蹦迪”这一行为,因此“不爱蹦迪”这一行为覆盖的世界就不存在了。在一部分可能性不复存在,而一部分可能性又在现实中受到限制的情况下,概率发生了 变化;
| 0.1 | 0.9 |
|---|---|
| 渣女爱蹦迪0.05 | 正经女孩爱蹦迪0.045=0.05*0.9 |
| 可能性消失(渣女不爱蹦迪) | 可能性消失(正经女孩不爱蹦迪) |
最初,4种世界的概率相加之和为1,但是由于不爱蹦迪的可能性不复存在,此时:渣女爱蹦迪、正经女孩爱蹦迪的概率相加之和便不等于1。为此,我们需要保持之前的比例关系,通过回复标准化条件,从而使概率发生变化。
(左边渣女爱蹦迪长边形面积):(右边正经女孩爱蹦迪长边形面积)=0.05:0.045=10:9;
10 19 = 0.523 \frac{10}{19}=0.523 1910=0.523
从上面我们可以看出,渣女爱蹦迪的概率为0.5263.这个概率,被称为“贝叶斯概率”。
渣男同理。
数学解释如下:
A = A= A=是渣女,B爱蹦迪
P ( A ) = 0.1 P(A)=0.1 P(A)=0.1 已知
P ( B ) = 0.05 + 0.045 = 0.095 P(B)=0.05+0.045=0.095 P(B)=0.05+0.045=0.095 已知
P ( A ∣ B ) = P P(A|B)=P P(A∣B)=P(在已经知道爱蹦迪的前提下,是渣女的概率)=要求的
P ( B ∣ A ) = P P(B|A)=P P(B∣A)=P(已经是渣女的情况下,爱蹦迪的概率)=P(渣女爱蹦迪)=0.05(已知)
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) = 0.1 0.05 0.095 = 0.5263 P(A|B)=P(A)\frac{P(B|A)}{P(B)}=0.1\frac{0.05}{0.095}=0.5263 P(A∣B)=P(A)P(B)P(B∣A)=0.10.0950.05=0.5263
3) 例二
4) 例三
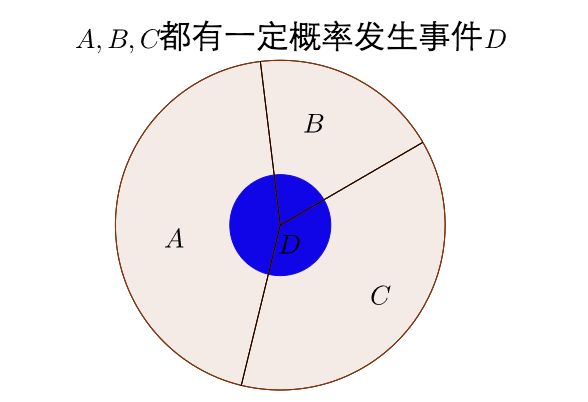
那贝叶斯定理到底是什么呢?
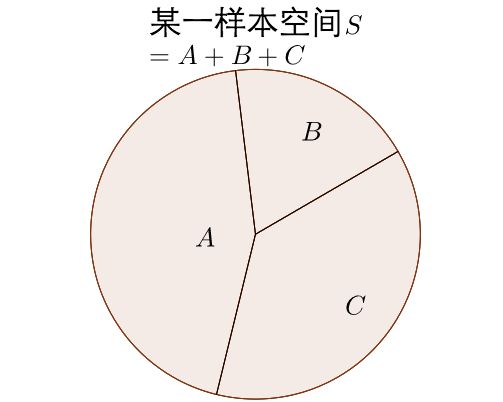
可见 P ( D ) = P ( D ∩ A ) + P ( D ∩ B ) + P ( D ∩ C ) P(D)=P(D\cap A) + P(D\cap B) + P(D\cap C) P(D)=P(D∩A)+P(D∩B)+P(D∩C)
由条件概率的公式也可以写成
P ( D ) = P ( D ∣ A ) P ( A ) + P ( D ∣ B ) P ( B ) + P ( D ∣ C ) P ( A C ) P(D)=P(D|A)P(A) + P(D|B)P(B) + P(D|C)P(AC) P(D)=P(D∣A)P(A)+P(D∣B)P(B)+P(D∣C)P(AC)
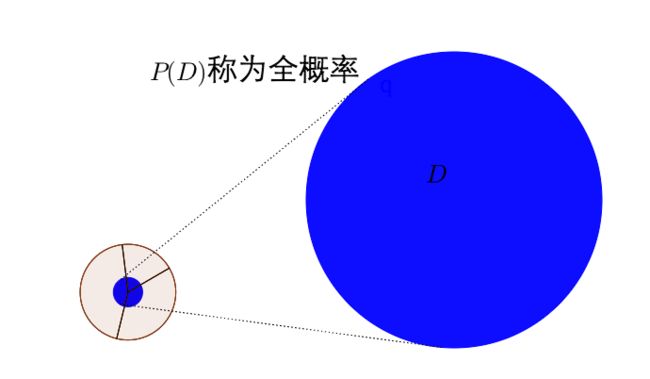
算出来的结果就是事件 D D D在样本空间 S S S下发生的概率。
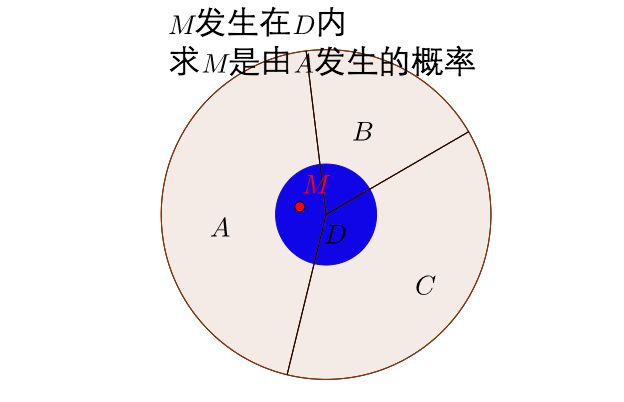
先发生 A A A再发生 D D D的事件
计算事件在样本空间下的概率
那么 M M M发生在 A A A中的概率
P ( A ∣ D ) = P ( A ∩ D ) P ( D ) P(A|D)=\frac{P(A\cap D)}{P(D)} P(A∣D)=P(D)P(A∩D)
= P ( D ∣ A ) P ( A ) P ( D ∣ A ) P ( A ) + P ( D ∣ B ) P ( B ) + P ( D ∣ C ) P ( A C ) =\frac{P(D|A)P(A)}{P(D|A)P(A) + P(D|B)P(B) + P(D|C)P(AC)} =P(D∣A)P(A)+P(D∣B)P(B)+P(D∣C)P(AC)P(D∣A)P(A)
这就是贝叶斯公式
6.0.6 全概率
6.1 贝叶斯分类器
概率知识+对决策带来的损失的认识→最优决策
6.1.1 贝叶斯判定准则
1) 期望损失(条件风险)R(x)
有 N N N种可能的标记,样本分类 Y = { c 1 , c 2 , . . . , c N } Y=\{c_1,c_2,...,c_N\} Y={c1,c2,...,cN}
λ i j \lambda_{ij} λij是将 c j c_j cj的样本错误的分类为 c i c_i ci所带来的损失
基于后验概率 P ( c j ∣ x ) P(c_j|x) P(cj∣x)可获得将样本 x x x分类为 c j c_j cj所产生的期望损失,即在样本 x x x上的条件风险
R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x) R(ci∣x)=j=1∑NλijP(cj∣x)
2) 最小条件风险的类别标记h(x)
任务是寻找一个判定标准 h : X → Y h:X\to Y h:X→Y以最小化风险(即在所有样本上的条件风险的期望)
总体风险 R ( h ) = E x [ R ( h ( x ) ∣ x ) ] R(h)=E_x[R(h(x)|x)] R(h)=Ex[R(h(x)∣x)](在所有样本上的条件风险的期望)
显然,对每个样本 x x x,若 h h h能最小化条件风险 R ( h ( x ) ∣ x ) R(h(x)|x) R(h(x)∣x),则总体风险 R ( h ) R(h) R(h)也将最小化,
这就产生了贝叶斯判定准则(Bayes decision rule)
为最小化总体风险,只需在每个样本上选择那个能使条件风险 R ( c ∣ x ) R(c|x) R(c∣x)最小的类别标记,即
h ∗ ( x ) = a r g m i n c ∈ y R ( c ∣ x ) h^*(x)=argmin_{c \in y}R(c|x) h∗(x)=argminc∈yR(c∣x)
h ∗ ( x ) h^*(x) h∗(x)叫做贝叶斯最优分类器,与之对应的总体风险 R ( h ∗ ) R(h^*) R(h∗)叫做贝叶斯风险, 1 − R ( h ∗ ) 1-R(h^*) 1−R(h∗)反映分类器所能到达的最好性能
3) 最小化分类错误率的贝叶斯最优分类器
具体来说,若目标是最小化分类错误率,把误判损失 λ i j \lambda_{ij} λij可写为
λ i j = { 0 , i = j 1 , o t h e r w i s e \lambda_{ij}=\begin{cases}0,i=j\\ 1,otherwise\end{cases} λij={0,i=j1,otherwise
此时条件风险
R ( c ∣ x ) = 1 − P ( c ∣ x ) R(c|x)=1-P(c|x) R(c∣x)=1−P(c∣x)
于是,最小化分类错误率的贝叶斯最优分类器为
h ∗ ( x ) = a r g m a x c ∈ Y P ( c ∣ x ) h^*(x)=argmax_{c\in Y}P(c|x) h∗(x)=argmaxc∈YP(c∣x)
即对每个样本 x x x,选择能使后验概率 P ( c ∣ x ) P(c|x) P(c∣x)最大的类别标记。
4) 问题描述
R ( c ∣ x ) = 1 − P ( c ∣ x ) h ∗ ( x ) = a r g m a x c ∈ Y P ( c ∣ x ) R(c|x)=1-P(c|x) \\ h^*(x)=argmax_{c\in Y}P(c|x) R(c∣x)=1−P(c∣x)h∗(x)=argmaxc∈YP(c∣x)
综上所述,问题转换为了基于有限的训练样本集尽可能准确地估计后验概率 P ( c ∣ x ) P(c|x) P(c∣x),求最小化条件风险即最大化后验概率。
欲使用贝叶斯判定准则来最小化决策风险,首先要获得后验概率P(c|x)。
然而,在现实任务中这通常难以直接获得。机器学习所要实现的是基于有限的训练样本集尽可能准确地估计出后验概率P(c|x)。所以得需要下面一个章节的极大似然估计
总结一下就是
分类问题被划分成了两个阶段:
推断inference阶段和决策decision阶段
- 推断阶段:使用训练数据学习后验概率
- 决策阶段:使用这些后验概率来进行最优的分类
现在呢???根据上面的计算。
基于贝叶斯准则,我们把分类问题转换成了 h ∗ ( x ) = a r g m a x c ∈ Y P ( c ∣ x ) h^*(x)=argmax_{c\in Y}P(c|x) h∗(x)=argmaxc∈YP(c∣x)
我们知道了想要进行分类,就必须得知道后验概率。
估计
后验概率主要有两种策略:
判别式模型(discriminative models):直接对类后验概率p(c|x)进行推断
P ( c ∣ x ) = P ( x , c ) p ( x ) P(c|x)=\frac{P(x,c)}{p(x)} P(c∣x)=p(x)P(x,c)
生成式模型(generative models):对**类条件概率P(x|c)和先验概率P©**进行推断。
P ( c ∣ x ) = P ( c ) P ( x ∣ c ) p ( x ) = P ( c ) P ( x ∣ c ) ∑ P ( c ) P ( x ∣ c ) P(c|x)=\frac{P(c)P(x|c)}{p(x)}=\frac{P(c)P(x|c)}{\sum P(c)P(x|c)} P(c∣x)=p(x)P(c)P(x∣c)=∑P(c)P(x∣c)P(c)P(x∣c)
根据现实,后验概率呢?很难获得。所以第一种策略行不通.
- 所以得需要
极大似然估计来估计类条件概率P(x|c) - 根据大数定理,当训练集样本包含充足的独立同分布样本时, P ( c ) P(c) P(c)可通过各类样本出现的概率进行估计
(条件风险 --> 后验概率 --> 先验概率和似然)
5) 常见问题
假设数据
λ i j = { 0 , i = j 1 , o t h e r w i s e \color{red}\lambda_{ij}=\begin{cases}0,i=j\\ 1,otherwise\end{cases} λij={0,i=j1,otherwise这句话啥意思呢???,是下面的意思
解释如下:
首先我们假定在买商品,商品生产出来优秀1,良好2,不及格3规格。
| 优秀1 | 良好2 | 不及格3 | |
|---|---|---|---|
| 优秀1 | 损失为0。 λ 优 秀 → 优 秀 = 0 \lambda_{优秀\to 优秀}=0 λ优秀→优秀=0因为本来就是优秀 | 损失为1. λ 优 秀 → 良 好 = 1 \lambda_{优秀\to 良好}=1 λ优秀→良好=1因为优秀的产品,被划分到不良好,卖亏了 | 损失为1.因为优秀的产品被划分到不及格,卖亏了 |
| 良好2 | 损失为1, λ 良 好 → 优 秀 = 1 \lambda_{良好\to 优秀}=1 λ良好→优秀=1。因为降低用户信任度 | 损失为0,因为本来就是良好 | 损失为1. |
| 不及格3 | 损失为1,因为不及格的产品被判断为优秀。降低用户信任度 | 损失为1.因为本来是不及格变成良好了,对用户是欺骗。降低用户信任度 | 损失为0,因为本来就是不及格 |
变成 λ i j \lambda_{ij} λij 就是下图
| 优秀1 | 良好2 | 不及格3 | |
|---|---|---|---|
| 优秀1 | λ 11 = 0 \lambda_{11}=0 λ11=0 | λ 12 = 1 \lambda_{12}=1 λ12=1 | λ 13 = 1 \lambda_{13}=1 λ13=1 |
| 良好2 | λ 21 = 1 \lambda_{21}=1 λ21=1 | λ 22 = 0 \lambda_{22}=0 λ22=0 | λ 32 = 1 \lambda_{32}=1 λ32=1 |
| 不及格3 | λ 31 = 1 \lambda_{31}=1 λ31=1 | λ 11 = 1 \lambda_{11}=1 λ11=1 | λ 33 = 0 \lambda_{33}=0 λ33=0 |
R ( c ∣ x ) = 1 − P ( c ∣ x ) \color{red}R(c|x)=1-P(c|x) R(c∣x)=1−P(c∣x)这句话啥意思呢???,
c 1 c_1 c1 代表优秀, c 2 c_2 c2代表良好, c 3 c_3 c3代表不及格
所以 P ( c 1 ∣ x ) + P ( c 2 ∣ x ) + P ( c 3 ∣ x ) = 1 P(c_{1}|x)+P(c_{2}|x)+P(c_{3}|x)=1 P(c1∣x)+P(c2∣x)+P(c3∣x)=1
首先由公式 R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x) R(ci∣x)=∑j=1NλijP(cj∣x)得
R ( c 优 秀 ∣ x ) = R ( c 1 ∣ x ) = λ 11 P ( c 1 ∣ x ) + λ 12 P ( c 2 ∣ x ) + λ 13 P ( c 3 ∣ x ) R(c_{优秀}|x)=R(c_{1}|x)=\lambda_{11}P(c_{1}|x)+\lambda_{12}P(c_{2}|x)+\lambda_{13}P(c_{3}|x) R(c优秀∣x)=R(c1∣x)=λ11P(c1∣x)+λ12P(c2∣x)+λ13P(c3∣x)
= 0 × P ( c 1 ∣ x ) + 1 × P ( c 2 ∣ x ) + 0 × P ( c 3 ∣ x ) =0\times P(c_{1}|x)+1\times P(c_{2}|x)+0\times P(c_{3}|x) =0×P(c1∣x)+1×P(c2∣x)+0×P(c3∣x)
= P ( c 2 ∣ x ) + P ( c 3 ∣ x ) =P(c_{2}|x)+P(c_{3}|x) =P(c2∣x)+P(c3∣x)
= 1 − P ( c 1 ∣ x ) =1-P(c_{1}|x) =1−P(c1∣x)
同理
R ( c 2 ∣ x ) = 1 − p ( c 2 ∣ x ) R(c_2|x)=1-p(c_2|x) R(c2∣x)=1−p(c2∣x)
R ( c 3 ∣ x ) = 1 − p ( c 3 ∣ x ) R(c_3|x)=1-p(c_3|x) R(c3∣x)=1−p(c3∣x)
看出 R ( c ∣ x ) = 1 − P ( c ∣ x ) R(c|x)=1-P(c|x) R(c∣x)=1−P(c∣x)
数学推导如下
P ( c 1 ∣ x ) + P ( c 2 ∣ x ) + . . . P ( c j ∣ x ) + . . . P ( c N ∣ x ) = 1 P(c_1|x)+P(c_2|x)+...P(c_j|x)+...P(c_N|x)=1 P(c1∣x)+P(c2∣x)+...P(cj∣x)+...P(cN∣x)=1
R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x) R(ci∣x)=∑j=1NλijP(cj∣x)
R ( c j ∣ x ) = 1 × P ( c 1 ∣ x ) + 1 × P ( c 2 ∣ x ) + . . . 0 × P ( c j ∣ x ) . . . + 1 × P ( c N ∣ x ) R(c_j|x)=1\times P(c_1|x)+1\times P(c_2|x)+...0\times P(c_j|x)...+1\times P(c_N|x) R(cj∣x)=1×P(c1∣x)+1×P(c2∣x)+...0×P(cj∣x)...+1×P(cN∣x)
R ( c j ∣ x ) = P ( c 1 ∣ x ) + P ( c 2 ∣ x ) + . . . 0 × P ( c j ∣ x ) . . . + P ( c N ∣ x ) R(c_j|x)= P(c_1|x)+ P(c_2|x)+...0\times P(c_j|x)...+P(c_N|x) R(cj∣x)=P(c1∣x)+P(c2∣x)+...0×P(cj∣x)...+P(cN∣x)
R ( c j ∣ x ) = 1 − P ( c j ∣ x ) R(c_j|x)=1-P(c_j|x) R(cj∣x)=1−P(cj∣x)
参考资料
https://www.zhihu.com/question/61298823/answer/1583165405
https://www.zhihu.com/question/19725590
https://www.matongxue.com/madocs/279/通俗地理解贝叶斯公式(定理) (biancheng.net)
https://zhuanlan.zhihu.com/p/42991859
(2条消息) 贝叶斯分类器原理——学习笔记_就是AT的博客-CSDN博客_贝叶斯分类器
https://blog.csdn.net/koulongxin123/article/details/123488232