CS224N WINTER 2022（五）Transformers详解（附Assignment5答案）

CS224N WINTER 2022（一）词向量（附Assignment1答案）
CS224N WINTER 2022（二）反向传播、神经网络、依存分析（附Assignment2答案）
CS224N WINTER 2022（三）RNN、语言模型、梯度消失与梯度爆炸（附Assignment3答案）
CS224N WINTER 2022（四）机器翻译、注意力机制、subword模型（附Assignment4答案）
CS224N WINTER 2022（五）Transformers详解（附Assignment5答案）

序言

• CS224N WINTER 2022课件可从https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1224/下载，也可从下面网盘中获取：

  https://pan.baidu.com/s/1LDD1H3X3RS5wYuhpIeJOkA
  提取码: hpu3
  

  本系列博客每个小节的开头也会提供该小结对应课件的下载链接。

• 课件、作业答案、学习笔记（Updating）：GitHub@cs224n-winter-2022

• 关于本系列博客内容的说明：

  • 笔者根据自己的情况记录较为有用的知识点，并加以少量见解或拓展延申，并非slide内容的完整笔注；

  • CS224N WINTER 2022共计五次作业，笔者提供自己完成的参考答案，不担保其正确性；

  • 由于CSDN限制博客字数，笔者无法将完整内容发表于一篇博客内，只能分篇发布，可从我的GitHub Repository中获取完整笔记，本系列其他分篇博客发布于（Updating）：

    CS224N WINTER 2022（一）词向量（附Assignment1答案）

    CS224N WINTER 2022（二）反向传播、神经网络、依存分析（附Assignment2答案）

    CS224N WINTER 2022（三）RNN、语言模型、梯度消失与梯度爆炸（附Assignment3答案）

    CS224N WINTER 2022（四）机器翻译、注意力机制、subword模型（附Assignment4答案）

    CS224N WINTER 2022（五）Transformers详解（附Assignment5答案）

---

---

lecture 9 Transformers

slides

[slides]

Transformer是对自然语言处理研究领域的一场革新，几乎目前NLP中所有的先进模型都离不开Transformer。典中典的Attention Is All You Need，很多人都有写过Transformer的原理解析，这里不赘述。

1. RNN的缺陷：slides p.19

   ① 线性交互距离（linear interaction distance）：联系两个相隔很长的节点的时间复杂度是$O(\text{sequence length})$

   ② 不能并行：GPU和TPU能够高效地并行巨量的独立运算，然而RNN无法享受这样的红利。

2. 自注意力（self attention）：slides p.22

   注意力机制将每个单词的表示视为查询向量（query），然后与一系列值向量结合（参考lecture7中相关内容），在encoder-decoder模型架构中，注意力得分是根据decoder中当前需要解码的一个隐层状态与encoder中所有隐层状态计算得到的一个相似度向量（如点积），这称为encoder-decoder注意力。

   自注意力则是encoder-encoder注意力（或decoder-decoder注意力），具体而言，在机器翻译模型中，注意力刻画的两种不同的语言序列（称之为输入语句和输出语句）之间的相似度，那么自注意力就是刻画输入语句（或输出语句）与自身的一个相似度。

   

3. Transformer的优势：slides p.24

   ① 非并行的运算复杂度不会随着序列长度的增加而增加；

   ② 因为自注意力机制的存在，每个单词都相互关联，因此联系两个相隔很长的节点的时间复杂度是$O(1)$

4. Transformer详解（编码器部分）：slides p.26

   下图摘自Transformer提出文：Attention Is All You Need

   

   • 自注意力机制：这是Transformer的核心区块（多头注意力）。

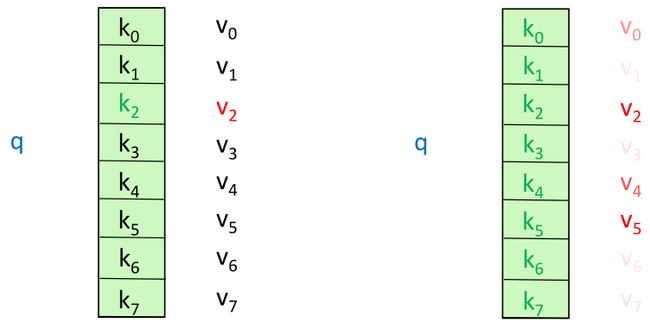
     假想有一个模糊的哈希表，如果我们想要查询某个值（value），我们需要将查询（query）与表中的键（key）进行对比（因为这是一个模糊的哈希表）。

     

     上图左边是各标准哈希表，每个查询恰好对应一个键值对，右边是自注意力机制，每个查询可能匹配多个键值对，因此我们将根据查询与键的相似度对每个值进行赋权。

     首先我们来看Transformer中编码器的自注意力机制：

     ① 对于每个输入的词向量$x_i\in {\mathbb{R}}^{d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$（$d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}$表示词向量的维度），计算其查询向量，键向量，值向量：
     $$q_i=W^Q{x}_i\in {\mathbb{R}}^{d_k}{k}_i=W^K{x}_i\in {\mathbb{R}}^{d_k}{v}_i=W^V{x}_i\in {\mathbb{R}}^{d_v}i=1,2,...,n\text{\hspace{1em}(9.1)}$$
     ② 计算查询向量与键向量之间的注意力得分（点积），$n$表示序列长度：
     $$e_{ij}=q_i{k}_j\in \mathbb{R}i=1,2,...,n;j=1,2,...,n\text{\hspace{1em}(9.2)}$$
     ③ 对注意力得分取softmax进行得到标准化的概率分布：
     $${\alpha }_{ij}=\text{softmax}(e_{ij})=\frac{\exp (e_{ij})}{{\sum }_{p=1}^n\exp (e_{ip})}\in \mathbb{R}i=1,2,...,n;j=1,2,...,n\text{\hspace{1em}(9.3)}$$
     ④ 根据概率分布计算值向量的加权累和：
     $${\text{output}}_i=\sum _{j=1}^n{\alpha }_{ij}{v}_{j}i=1,2,...,n\text{\hspace{1em}(9.4)}$$
     可以将式$(9.1)$到式$(9.4)$写成统一矩阵的形式：
     $$\begin{array}{rl}Q=X{W}^{Q}K=X{W}^{K}V=X{W}^V& \\ E=Q{K}^{\top }& \\ A=\text{softmax}(E)& \\ \text{Output}=AV& \end{array}\}\Rightarrow \text{Output}=\text{softmax}(Q{K}^{\top })V\text{\hspace{1em}(9.5)}$$
     其中：
     $$\begin{gathered} X\in {\mathbb{R}}^{n\times d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}},W^Q\in {\mathbb{R}}^{d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times d_k},W^K\in {\mathbb{R}}^{d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times d_k},W^V\in {\mathbb{R}}^{d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times d_v} \\ Q\in {\mathbb{R}}^{n\times d_k},K\in {\mathbb{R}}^{n\times d_k},V\in {\mathbb{R}}^{n\times d_v},E\in {\mathbb{R}}^{n\times n},A\in {\mathbb{R}}^{n\times n},\text{Output}\in {\mathbb{R}}^{n\times d_v}\text{\hspace{1em}(9.6)} \end{gathered}$$
     现在的问题在于是式$(9.5)$的注意力的机制中仅仅是对值向量做加权平均，缺少元素级别上的非线性成分，一种简单的处理思路是将式$(9.7)$直接输入到一个前馈层中，然后使用非线性的激活函数处理一下即可：
     $$m_i=\text{MLP}({\text{output}}_i)=W_2\times \text{ReLU}(W_1\times {\text{output}}_i+b_1)+b_2\text{\hspace{1em}(9.7)}$$
     下面要介绍的是编码器中的几个技巧：

   • 训练技巧一：残差连接（Residual Connections）：$x_l=F(x_{l-1})+x_{l-1}$

     这是为了防止网络忘记多层之前的重要信息，因此直接粗暴地把多层之前的信息$x_{l-1}$拎过来。

     残差连接也可以使得损失函数的更新更加平滑（缓解梯度消失），使得训练更加丝滑流畅。

   • 训练技巧二：层标准化（LayerNorm）：

     层正则化是将网络层的输入划归为均零方一的格式：
     $${x^l}^{\prime }=\frac{x^l-{\mu }^l}{{\sigma }^l+ϵ}\text{\hspace{1em}(9.8)}$$
     分母添加的小常数$ϵ$是为了防止标准差过小。

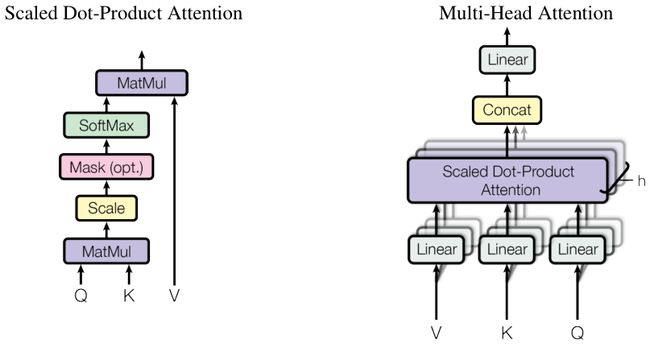
   • 训练技巧三：Scaled Dot-product Attention

     式$(9.5)$即Dot-product Attention，原论文中提出归一化，即得到原文Figure2中的Scaled Dot-product Attention：
     $$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^{\top }}{\sqrt{d_k}}\right)V\text{\hspace{1em}(9.9)}$$
     这里其实就是一个层标准化，因为均值是零，$\sqrt{d_k}$就是标准差。

   • 位置编码（Positional Encodings）：slides p.39

     是否注意到目前为止，输入序列的次序并不会影响上面每一个表达式的求解，也就是说我将一个输入语句打乱次序，上面的计算结果仍然保持不变。因此需要引入位置编码（这是Transformer扯下RNN的最后一块遮羞布，RNN可以表达次序，Transformer也完美解决了这个问题）。

     在式$(9.1)$的基础上，我们定义$p_i\in {\mathbb{R}}^d$（$i=1,2,...,n$）来编码位置编号，然后更新：
     $$\begin{gathered} v_i\leftarrow v_i+p_i \\ {q}_i\leftarrow q_i+p_i \\ {k}_i\leftarrow k_i+p_i\text{\hspace{1em}(9.10)} \end{gathered}$$
     这里有一个小问题就是$v_i\in {\mathbb{R}}^{d_v}$的维度跟$q_i,k_i\in {\mathbb{R}}^{d_k}$可能是不一样的，式$(9.10)$可能没那么容易就可以相加，但是这不关键，因为$p_i$的定义是这样的：
     $$p_i=\left[\begin{array}{c}\sin (i/10000^{2/d})\\ \sin (i/10000^{2/d})\\ \sin (i/10000^{4/d})\\ \cos (i/10000^{4/d})\\ ...\\ \sin (i/10000^{2\times (d/2)/d})\\ \cos (i/10000^{2\times (d/2)/d})\end{array}\right]\in {\mathbb{R}}^d\text{\hspace{1em}(9.11)}$$
     因此只要自定义一下$d$的取值即可，想要多少维度的的$p_i$都可以。这样的位置编码其实本质上就是就是近似的交替$[0,1,0,1,...0,1]$，与绝对位置基本已经没有太大关系了。

     其实对于式$(9.11)$这种定义许多人颇有微词，认为这种定义的位置编码不具有可学习性（其实就已经完全固定了），因此也有人觉得应当将$p_i$变为可学习的参数，比如学习一个$p\in {\mathbb{R}}^{d\times n}$来作为位置编码的嵌入表示。这样的好处是确实可以学习到更好的位置编码，但是坏处是无法外推到文本序列长度超过$n$的情况。

     一些近期的位置编码研究paper：相对线性位置编码，结构化的位置编码

   • 多头注意力机制：slides p.44

     

     多头注意力机制是在式$(9.9)$的基础上进行的改进，简而言之就是重复做若干次Scaled Dot-product Attention，得到多个头（head）$\mathrm{O}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t}$，将它们拼接起来后再进行一次线性映射：
     $$\begin{gathered} \text{MultiHead}(Q,K,V)=\text{Concat}({\text{head}}_1,...,{\text{head}}_h)W^O\in {\mathbb{R}}^{n\times d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}} \\ {\text{head}}_i=\text{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)\in {\mathbb{R}}^{n\times d_v}i=1,2,...,h\text{\hspace{1em}(9.12)} \end{gathered}$$
     其中$W^O\in {\mathbb{R}}^{h{d}_v\times d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$，$h=8,d_k=d_v=d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}/h=64$是默认的超参数。

     使用多头注意力的原因可以这样解释，一个头所揭示的概率分布权重可能并不那么可信，那么我就多做几个不同的头，让它们学习得到一个更好的权重表示。

5. Transformer详解（解码器部分）以及缺陷分析：slides p.47

   • Masked多头注意力：如何避免解码器作弊（解码器逐字解码，要防止其使用到整个序列的信息），因此使用Masked Multi-Head Attention（这个在assignment4中代码部分有一个类似的问题，需要回答mask的作用，答案就是防止作弊），将未来的分词信息给抹去。

     

   • encoder-decoder注意力机制：

     相对于编码器中的自注意力（键、值、查询）都来自同一个语句序列，解码器中的注意力机制就跟lecture7中讲得没什么两样了（来自两个语句序列的相似度计算注意力得分）：

     ① $h_1,...,h_n\in {\mathbb{R}}^d$是编码器的输出向量；

     ② $z_1,...,z_n\in {\mathbb{R}}^d$是解码器的输入向量；

     ③ 记录$k_i=K{h}_i,v_i=V{h}_i,i=1,...,n$

     ④ 计算$q_i=Q{z}_i,i=1,...,n$

   总体来说Transformerd的缺陷可能主要在于这样几点：

   • 位置编码的做法存在争议，这个在上文已有几篇改进做法paper的链接；

   • 关于自注意力需要计算$O(n^2)$对自注意力权重太耗时，有人提出改进Linformer到$O(n)$的级别，核心思想是将序列长度$n$映射到低维；

     还有人（bigbird，这个链接是错的，但是也没能确定到底是哪一篇，叫题目里带bigbird的还挺多，基本都不是NLP领域的）直接就少算一些自注意力得分：

     

suggested readings

1. 期末项目第一个默认项目的指导，关于经典的SQuAD问答数据集，代码在GitHub@squad，包含了代码说明、基线模型训练、如何提交结果到排行榜等工作。（Project Handout (IID SQuAD track)）
2. 期末项目第二个默认项目的指导，也是关于SQuAD问答数据集，代码在GitHub@robustqa，这个主要是考察问答系统的鲁棒性。（Project Handout (Robust QA track)）
3. Transformer提出文，梦的开始。（Attention Is All You Need）
4. 图文并茂讲解Transformer的一篇博客。（The Illustrated Transformer）
5. GoogleAI发布Transformer的介绍博客。（Transformer (Google AI blog post)）
6. 层正则化技术的提出文。（Layer Normalization）
7. 用于图像处理的Transformer（Image Transformer）
8. 用于音频处理的Transformer（Music Transformer: Generating music with long-term structure）

---

lecture 10 更多关于Transformers的内容以及预训练

slides

[slides]

1. 爆炸性新闻：slides p.2-3

   • 2022/02/19：AlphaCode（基于Transformer的预训练代码生成模型）在Codeforces programming比赛中取得了54.3%的准确率。
   • 2021/09/20：miniF2F（基于Transformer的数学证明生成模型）在collection of challenging math Olympiad questions取得了突破性进展（29.3%提升到41.2%）。正式论文链接

2. 关于单词结构：slides p.9

   这里提到或许Transformer中也可以考虑使用subword级别的编码，问题在于一定要能编纂出一个很好的subword字典（中文可以用偏旁部首，英文要有前后缀等等）。

3. 预训练词向量：slides p.24

   Semi-supervised Sequence Learning可能是比较早提出预训练概念的paper，这里使用的就是语言模型的策略，即预测下一个单词，那么就构建一个解码器模型来预测语句中的下一个单词，最后将整个语句预测出来，得到的一个预训练好的模型再嫁接到NLP任务的模型中继续训练（相当于预先找好一个模型参数的初始点）。

4. 预训练的三种方法：slides p.27

   

   • 解码器模型：即预先训练一个用于解码隐层状态的模型，如GPT-2，GPT-3，LaMDA；

     通常使用语言模型来预训练解码器，经典的GPT模型与GPT2模型是对Transformer的解码器进行预训练（12层），768个隐层状态，3072维的前馈隐层，使用的是Byte-pair编码（属于subword级别的编码），训练语料是BooksCorpus（超过7000本书籍，包含大量的长文本）。并在多个自然语言生成数据集上进行了测试，效果拔群。

     GPT-2模型在GPT模型的基础上继续增加训练数据。

     GPT-3是更大的一个模型（1750亿的参数）。

   • 编码器模型：即预先郧县一个用于编码文本输入的模型，如BERT，RoBERTa；

     BERT在推荐阅读的第一篇（BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding），它的预训练任务是预测被mask掉（80%）、被随机替换（10%）、保持原样（10%）的单词。也是在BookCorpus和Wikipedia上训练的，64张TPU用时4天训练得到，基础模型（12层，768维隐层状态，12注意力头，1.1亿参数），大模型（24层，1024维一层状态，16注意力头，3.4亿参数）。

     缺陷：如果主任务是要生成序列，通常选择使用GPT这类预训练的解码器，BERT并不太适合用于序列自动生成类（一次解码一个单词的那种）的任务。

     变体：RoBERTa，SpanBERT

   • 编码器解码器模型：如Transformer，T5，Meena；

     The encoder portion benefits from bidirectional context; the decoder portion is used to train the whole model through language modeling.

     意思应该是，编码器得到最终隐层状态输入解码器，与解码器的输入合并，然后解码器还是一个语言模型，任务就是预测下一个单词。其中编码器的输入是$(w_1,...,w_T)$，解码器的输入是$(w_{T+1},w_{T+2},...,w_{2T})$，解码器的输出是$(w_{T+2},w_{T+3},...,w_{2T+1})$

     推荐的一篇使用了这种类型预训练模型的paper

     T5模型是问答模型的一种预训练模型，可以用来进行微调解决很多问答任务。

suggested readings

1. BERT提出文，梦的升华。（BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding）
2. 这是一篇偏讲授性质的paper，关于上下文嵌入，适合作为教材学习（Contextual Word Representations: A Contextual Introduction）
3. 关于BERT，ELMo的图文讲解博客。（The Illustrated BERT, ELMo, and co.）
4. 教材中关于上下文嵌入在迁移学习中应用的内容。（Martin & Jurafsky Chapter on Transfer Learning）

huggingface transformers tutorial session

[Colab]

关于Transformer的教程可以查看笔者的博客，这个Notebook需要才能看到。

assignment5 参考答案

[code] [handout] [latex template]

Assignment5参考答案（written+coding）：囚生CYのGitHub Repository

本次作业不确定性较大，因为缺少计算资源无法完全跑通所有代码。

1. Attention exploration

• $(a)$ 提示：参考[slides]中注意力机制的相关内容。

  • $(1)$ 作业中式$(1)$已经写得很明白了，这是一个模糊查询，我们不能直接通过查询向量$q$精确匹配到某个键向量$k$，只能赋予每个键一定的概率分布权重（即${\alpha }_{ij}$），得到最终的输出结果。
  • $(2)$ 根据式$(2)$的计算方法，如果查询向量$q$与某个键$k_i$的相似度非常高（点积值很大），且$q$与其他的键基本垂直（点积值为零），那么就会使得${\alpha }_i$极大。
  • $(3)$ 此时$c$基本近似等于$v_i$
  • $(4)$ 直觉上就是单词的表示越相近，注意力权重就会越高，得到的注意力输出就越接近那个单词。（感觉在把一句废话换着方式说了好几遍）

• $(b)$ 只考虑两个值向量的特殊情况，探究注意力机制的深层含义。

  • $(1)$ 有人可能会觉得如果只是将值向量根据注意力得分取加权和，很难从这个结果中挖掘原先值向量的信息，事实上不然，但是这里做了一个非常强的假定，即两个值向量$v_a,v_b$是来自相互垂直的向量空间的：
    $$\begin{gathered} v_a\in \text{span}\{a_1,a_2,...,a_m\}\Rightarrow v_a=\sum _{i=1}^m{c}_i{a}_i \\ {v}_b\in \text{span}\{b_1,b_2,...,b_p\}\Rightarrow v_b=\sum _{j=1}^p{d}_i{b}_i \\ \text{where }\{\begin{array}{rlrl}& a_i^{\top }{b}_j=0& & \forall i=1,...,m;\forall j=1,...,p\\ & a_i^{\top }{a}_j=0& & \forall i=1,...,m\\ & b_i^{\top }{b}_j=0& & \forall j=1,...,p\end{array}\text{\hspace{1em}(a5.1.1)} \end{gathered}$$
    根据秩一矩阵的构造方法，假定$M$具有如下的形式：
    $$M=\sum _{i=1}^m{\lambda }_i{a}_i{a}_i^{\top }\text{\hspace{1em}(a5.1.2)}$$
    其中${\lambda }_i,i=1,...,m$是待定系数，则有如下推导：
    $$\begin{array}{rl}Ms=v_a& ⟺M(v_a+v_b)=v_a\\ & ⟺\left(\sum _{i=1}^m{\lambda }_i{a}_i{a}_i^{\top }\right)\left(\sum _{i=1}^m{c}_i{a}_i+\sum _{j=1}^p{d}_i{b}_i\right)=\sum _{i=1}^m{c}_i{a}_i\\ & ⟺\sum _{i=1}^m{\lambda }_i{c}_i{a}_i{a}_i^{\top }{a}_i=\sum _{i=1}^m{c}_i{a}_i\text{(orthogonal property)}\\ & ⟺\sum _{i=1}^m({\lambda }_i{c}_i{a}_i^{\top }{a}_i)a_i=\sum _{i=1}^m{c}_i{a}_i\\ & ⟹{\lambda }_i{c}_i{a}_i^{\top }{a}_i=c_i\\ & ⟹{\lambda }_i=\frac{1}{a_i^{\top }{a}_i}i=1,...,m\end{array}\text{\hspace{1em}(a5.1.3)}$$
    综上所述：
    $$M=\sum _{i=1}^m\frac{a_i{a}_i^{\top }}{a_i^{\top }{a}_i}\text{\hspace{1em}(a5.1.4)}$$

  • 本质上就是找一个$q$使得$k_a^{\top }q=k_b^{\top }q$，则可知$q^{\top }(k_a-k_b)=0$，找一个与$k_a-k_b$垂直的$q$就完事了（表达式应该怎么写呢？）。

• $(c)$ 探究单头注意力机制的缺陷：

  • $(1)$ 因为协方差矩阵很小，因此可以近似用${\mu }_i$来替换$k_i$，因此等价于找一个$q$与$({\mu }_a-{\mu }_b)$垂直即可。
  • $(2)$ 容易想到，如果存在一个明显很大的键向量$k_a$，那么单头注意力机制得到的权重就没有什么意义了，因为加权和之后基本就还是指向$k_a$的方向。

• $(d)$ 探究多头注意力机制的优势：

  这里的意思是说，给两个查询向量$q_1$和$q_2$，分别计算单头注意力得到权重$c_1$和$c_2$，然后取$c=(c_1+c_2)/2$作为最终结果即可。

  • $(1)$ 这个就没那么显然了，要求有下式的条件成立：
    $$\begin{array}{rl}& {\alpha }_1^a+{\alpha }_2^a={\alpha }_1^b+{\alpha }_2^b\\ ⟺& \frac{\exp (k_a^{\top }{q}_1)}{\exp (k_a^{\top }{q}_1)+\exp (k_b^{\top }{q}_1)}+\frac{\exp (k_a^{\top }{q}_2)}{\exp (k_a^{\top }{q}_2)+\exp (k_b^{\top }{q}_2)}=\frac{\exp (k_b^{\top }{q}_1)}{\exp (k_a^{\top }{q}_1)+\exp (k_b^{\top }{q}_1)}+\frac{\exp (k_b^{\top }{q}_2)}{\exp (k_a^{\top }{q}_2)+\exp (k_b^{\top }{q}_2)}\\ ⟺& \frac{\exp (k_a^{\top }{q}_1)-\exp (k_b^{\top }{q}_1)}{\exp (k_a^{\top }{q}_1)+\exp (k_b^{\top }{q}_1)}+\frac{\exp (k_a^{\top }{q}_2)-\exp (k_b^{\top }{q}_2)}{\exp (k_a^{\top }{q}_2)+\exp (k_b^{\top }{q}_2)}=0\\ ⟺& [\exp (k_a^{\top }(q_1+q_2))+\exp (k_a^{\top }{q}_1+k_b^{\top }{q}_2)-\exp (k_b^{\top }{q}_1+k_a^{\top }{q}_2)-\exp (k_b^{\top }(q_1+q_2))]\\ & +[\exp (k_a^{\top }(q_1+q_2))+\exp (k_b^{\top }{q}_1+k_a^{\top }{q}_2)-\exp (k_a^{\top }{q}_1+k_b^{\top }{q}_2)-\exp (k_b^{\top }(q_1+q_2))]=0\\ ⟺& \exp (k_a^{\top }(q_1+q_2))=\exp (k_b^{\top }(q_1+q_2))\\ ⟺& k_a^{\top }(q_1+q_2)=k_b^{\top }(q_1+q_2)\\ ⟺& (k_a-k_b{)}^{\top }(q_1+q_2)=0\end{array}\text{\hspace{1em}(a5.1.5)}$$
    刚好消掉了交叉项，那么结论就是找到$q_1,q_2$使得它们的和与$k_a-k_b$垂直，这里用${\mu }_a$和${\mu }_2$近似，就是跟${\mu }_a-{\mu }_b$垂直。

  • $(2)$ 实话说没怎么搞明白是什么意思，虽然增加了协方差，但是${\mu }_a-{\mu }_b$依然可以近似表示$k_a-k_b$，而且理论上偏差值比没有协方差的情况要小一些（因为协方差都是正数，所以相减相当于抵消了一些偏差）。

    我觉得可能就是想说在多头注意力的情况下，可以缓解$(c.2)$的问题，因为对输出的注意力权重进行了均衡。

2. Pretrained Transformer models and knowledge access

本次代码实验是$\text{GPT}$模型的预训练和微调，$\text{GPT}$模型定义的代码已经完全写好了，要完成的只是数据处理、注意力机制定义、运行与报告部分的代码。

注意代码里有不少读取文件的默认代码可能出错，需要设置文件编码类型。

实话说这个任务有点离谱，居然是根据人名预测出生地，虽说的确不同地区的人名是可以做一些区分，但未免也太牵强了。

本题的代码借鉴自GitHub@Mr-maoge的解法，需要至少$8\text{G}$以上的显存才能跑通，因为缺少计算资源无法跑通代码（经测试，可以调小$\text{batch size}$使得在低显存耗用的情况下通过代码测试，但是无法获得正确的结果）。

虽然代码很难跑通得到结果，但是其中的$\text{GPT}$模型代码以及两种注意力机制的实现代码是值得学习的。

• $(a)$ 阅读play_char.ipynb，看代码说明里应该还有play_math.ipynb，play_image.ipynb，play_word.ipynb，有谁知道几个在哪儿可以找到，到时候踢我一下。

• $(b)$ 运行python src/dataset.py namedata得到以下输出：

  data has 418352 characters, 256 unique.
  x: Where was Khatchig Mouradian born?⁇Lebanon⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  y: □□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□⁇Lebanon⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  x: Where was Jacob Henry Studer born?⁇Columbus⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  y: □□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□⁇Columbus⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  x: Where was John Stephen born?⁇Glasgow⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  y: □□□□□□□□□□□□□□□□□□□□□□□□□□□⁇Glasgow⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  x: Where was Georgina Willis born?⁇Australia⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  y: □□□□□□□□□□□□□□□□□□□□□□□□□□□□□□⁇Australia⁇□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
  

  双问号表示MASK_CHAR，正方形表示PAD_CHAR。

• $(c)$ 编写run.py中相关代码块，注意如果出现trainer.py中有pipeline的报错信息，将num_workers取$0$来避免。（从这边往下$\text{PC}$机就跑不通了）

• $(d)$ 运行下面的脚本：

  # Train on the names dataset
  python src/run.py finetune vanilla wiki.txt --writing_params_path vanilla.model.params --finetune_corpus_path birth_places_train.tsv
  # Evaluate on the dev set, writing out predictions
  python src/run.py evaluate vanilla wiki.txt --reading_params_path vanilla.model.params --eval_corpus_path birth_dev.tsv --outputs_path vanilla.nopretrain.dev.predictions
  # Evaluate on the test set, writing out predictions
  python src/run.py evaluate vanilla wiki.txt --reading_params_path vanilla.model.params --eval_corpus_path birth_test_inputs.tsv --outputs_path vanilla.nopretrain.test.predictions
  

• $(e)$ 运行python src/dataset.py charcorruption

• $(f)$ 运行下面的脚本：

  # Pretrain the model
  python src/run.py pretrain vanilla wiki.txt --writing_params_path vanilla.pretrain.params
  # Finetune the model
  python src/run.py finetune vanilla wiki.txt --reading_params_path vanilla.pretrain.params --writing_params_path vanilla.finetune.params --finetune_corpus_path birth_places_train.tsv
  # Evaluate on the dev set; write to disk
  python src/run.py evaluate vanilla wiki.txt --reading_params_path vanilla.finetune.params --eval_corpus_path birth_dev.tsv --outputs_path vanilla.pretrain.dev.predictions
  # Evaluate on the test set; write to disk
  python src/run.py evaluate vanilla wiki.txt --reading_params_path vanilla.finetune.params --eval_corpus_path birth_test_inputs.tsv --outputs_path vanilla.pretrain.test.predictions
  

• $(g)$ 运行下面的脚本：

  # Pretrain the model
  python src/run.py pretrain synthesizer wiki.txt --writing_params_path synthesizer.pretrain.params
  
  # Finetune the model
  python src/run.py finetune synthesizer wiki.txt --reading_params_path synthesizer.pretrain.params --writing_params_path synthesizer.finetune.params --finetune_corpus_path birth_places_train.tsv
  
  # Evaluate on the dev set; write to disk
  python src/run.py evaluate synthesizer wiki.txt --reading_params_path synthesizer.finetune.params --eval_corpus_path birth_dev.tsv --outputs_path synthesizer.pretrain.dev.predictions
  
  # Evaluate on the test set; write to disk
  python src/run.py evaluate synthesizer wiki.txt --reading_params_path synthesizer.finetune.params --eval_corpus_path birth_test_inputs.tsv --outputs_path synthesizer.pretrain.test.predictions
  

  记录一下$\text{synthesizer}$注意力（提出论文）的原理：

  • 设$X\in {\mathbb{R}}^{l\times d}$，其中$l$的块大小（序列长度），$d$是词向量温度，$d/h$是每个注意力头的维度，$Q,K,V\in {\mathbb{R}}^{d\times d/h}$跟自注意力中的三个矩阵一样，则自注意力头的输出为：
    $$Y_i=\text{softmax}\left(\frac{(X{Q}_i)(X{K}_i{)}^{\top }}{\sqrt{d/h}}\right)(X{V}_i)\in {\mathbb{R}}^{l\times d/h}\text{\hspace{1em}(a5.2.1)}$$
    接着将各个自注意力头拼接起来：
    $$Y=[Y_1;...;Y_h]A\in {\mathbb{R}}^{l\times d}\text{\hspace{1em}(a5.2.2)}$$

  • 本题实现的是上面的一个变体：
    $$Y_i=\text{softmax}(\text{ReLU}(X{A}_i+b_1)B_i+b_2)(X{V}_i)\text{\hspace{1em}(a5.2.3)}$$
    其中$A_i\in {\mathbb{R}}^{d\times d/h},B\in {\mathbb{R}}^{d/h\times l},V_i\in {\mathbb{R}}^{d\times d/h}$

    可以作这样的解释：

    ① $(X{Q}_i)(X{K}_i{)}^{\top }\in {\mathbb{R}}^{l\times l}$是注意力得分；

    ② $\text{synthesizer}$变体则避免计算所有成对的这种点积，而是直接通过将每个自注意力头的$d$维向量映射到$l\times l$的注意力得分矩阵。

3. Considerations in pretrained knowledge

• $(a)$ 预训练模型结果比非预训练模型结果好不是理所当然的吗，硬要说就是首先找到了一个比较好的初始解开始迭代，因而可以收敛到更好地解。实际情况，不微调只有$0.02$，微调了之后是$0.22$
• $(b)$ 人无法辨别出机器到底是检索还是在瞎猜，这可能会使得机器的可解释性下降，无法用于实际应用。测试集中几乎所有人名都没有在训练集中出现过，但是只看姓氏或者名字的话还是有迹可循的，所以机器也并非完全是在瞎猜。
• $(c)$ 模型瞎猜肯定会导致应用的可信度下降呗，不是很能理解这种应用有啥用。