独孤九剑第八式-DBSCAN聚类模型（密度聚类模型）

文章适合于所有的相关人士进行学习
各位看官看完了之后不要立刻转身呀
期待三连关注小小博主加收藏
小小博主回关快 会给你意想不到的惊喜呀
各位老板动动小手给小弟点赞收藏一下，多多支持是我更新得动力！！！

---

前言

前面我们介绍了K-means这种无监督的机器学习聚类算法，核心思想就是一次又一次的确定数据点的平均值然后对每一个均值点进行分类，最后趋于稳定后就表示聚类完成。本章我们将讲解另外一种无监督的聚类算法，这节就非常非常简单啦，因为没有目标函数了，理解起来也比较容易。函数也比较简单，所以我们直接进入正题吧。

DBSCAN密度聚类算法思想讲解

K-means聚类算法的缺点

我们上次所介绍的K-means算法主要有两个缺点，第一就是容易受到异常值的影响，比如说有三个人一个人的工资是1000，一个人是1500，另外一个是10000元。那么我要在他们之间取均值，那么对于赚1000元的人就不太准确了。第二就是无法准确的对非球形簇进行合理的聚类。

DBSCAN聚类算法思想

但是DBSCAN密度聚类算法就可以解决非球形簇的分类问题。“密度”可以理解为样本点的紧密程度，如果在指定的半径领域内，实际样本量超过给定的最小样本量阈值，则认为是密度高的对象，就可以聚成一个簇。

DBSCAN聚类算法的相关概念

点的半径领域：在某点p处，给定其半径e后，所得到的覆盖区域。
核心对象：对于给定的最少样本量MinPts而言，如果某一点p的e领域内至少包括MinPts个样本点，那么点p就是核心对象。
直接密度可达：假设点p为核心对象，且在点p的e领域内存在点q，则从点p出发到q是直接密度可达的。
密度可达：假设存在一系列的对象链p1，p2…pn，如果p1是关于半径e和最少样本点MinPts的直接密度可达Pi+1,则p1密度可达pn。
密度相连：假设点o为核心对象，从o出发得到两个密度可达点p和点q，则称点q和点p是密度相连的
聚类的簇：簇包含了最大的密度相连所构成的样本点。
边界点：假设点p为核心对象，在其领域内包含了点b，如果点b为非核心对象，则称其为点p的边界点。
异常点：不属于任何簇的节点。

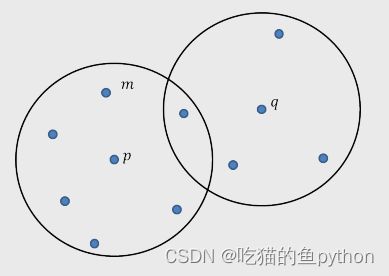
如图假设半径为3，最小样本点设为7.
那么p就是核心对象，q就不是核心对象（因为最小样本点为5，不满足7）。m点就是p点的直接密度可达。

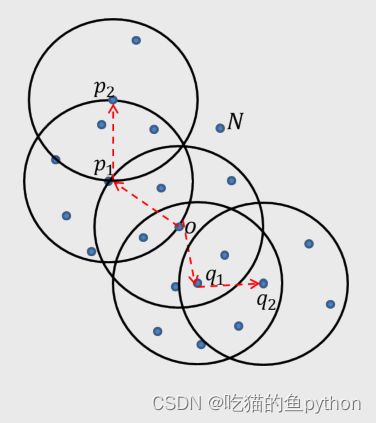
这里我们依旧设置半径为3，最小样本点设为7.
N点就是异常点，p1是核心对象，p2不是核心对象，那么我们就说p2是p1的临界点。

DBSCAN聚类算法的步骤讲解

1.为密度聚类算法设置一个合理的半径区域和包含最小的样本量MinPts。
2.从数据集中随机挑选一个样本点p，检验其在半径领域是否包含最小样本量，如果包含那么就定性为核心对象，并构成一个簇C，如果不包含，那么重新挑选一个样本点。
3.对于核心对象p所覆盖的其他样本q，如果点q对应的半径领域内仍然包含最小样本量，就将其覆盖的样本点统统归于簇C。
4.重复步骤3，将最大的密度相连所包含的样本点聚为一类，形成一大簇。
5.完成步骤4后，重新回到步骤2，并重复步骤3，4，直到没有新簇形成为止。

DBSCAN聚类算法的函数介绍

cluster.DBSCAN(eps=0.5, min_samples=5, metric=‘euclidean’, p=None)

eps：用于设置密度聚类中的e领域，即半径，默认为0.5
min_samples：用于设置e领域内最少的样本量，默认为5
metric：用于指定计算点之间距离的方法，默认为欧氏距离
p：当参数metric为闵可夫斯基（‘minkowski’）距离时，p=1，表示计算点之间的曼哈顿距离；p=2，表示计算点之间的欧氏距离；该参数的默认值为2

DBSCAN密度聚类算法和K-means算法比较

我们设定两个簇，然后使用K-means聚类算法进行聚类结果是：

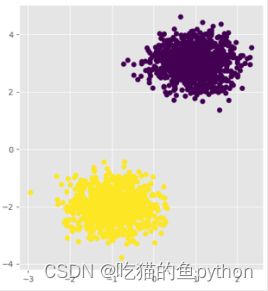
DBSCAN聚类算法结果是：

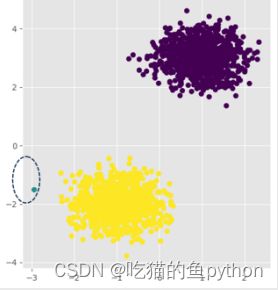
和明显，把异常点分了出来。我们在来看一组：
K-means（缺点出来了，无法对非球形簇合理分类）

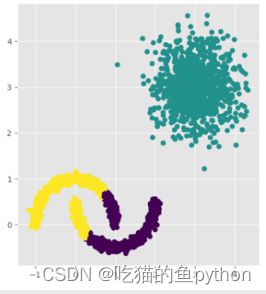
DBSCAN聚类算法结果是：

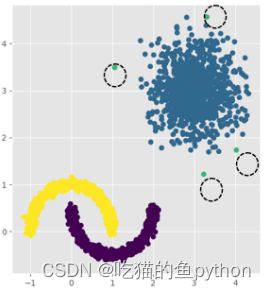
基本完美聚类。
这里我们怎么确定半径和最小样本量呢？我们之前学过网格法，思路大体一致，于是我们设定了一个算法来确定最优的值：

DBSCAN密度聚类算法实战

数据

我们对各省份的出生率和死亡率做聚类，来分析哪里适合居住。

画散点图

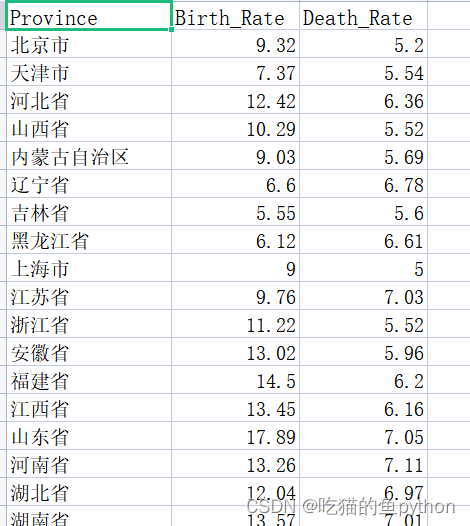
Province = pd.read_excel(r'Province.xlsx')
Province.head()
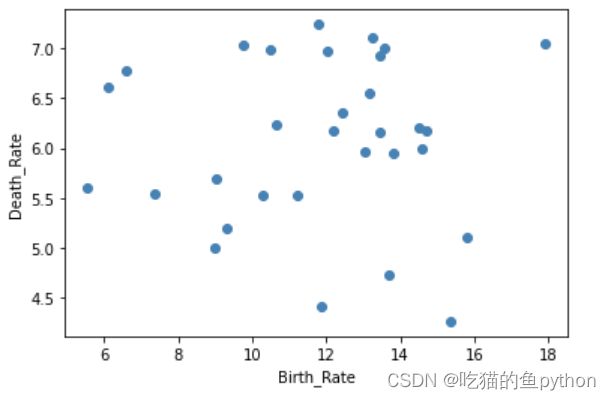
# 绘制出生率与死亡率散点图
plt.scatter(Province.Birth_Rate, Province.Death_Rate, c = 'steelblue')
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
# 显示图形
plt.show()

分析如何确定半径和最小样本量

res = []
# 迭代不同的eps值
for eps in np.arange(0.001,1,0.05):
    # 迭代不同的min_samples值
    for min_samples in range(2,10):
        dbscan = cluster.DBSCAN(eps = eps, min_samples = min_samples)
        # 模型拟合
        dbscan.fit(X)
        # 统计各参数组合下的聚类个数（-1表示异常点）
        n_clusters = len([i for i in set(dbscan.labels_) if i != -1])
        # 异常点的个数
        outliners = np.sum(np.where(dbscan.labels_ == -1, 1,0))
        # 统计每个簇的样本个数
        stats = str(pd.Series([i for i in dbscan.labels_ if i != -1]).value_counts().values)
        res.append({'eps':eps,'min_samples':min_samples,'n_clusters':n_clusters,'outliners':outliners,'stats':stats})
# 将迭代后的结果存储到数据框中        
df = pd.DataFrame(res)
df

方法就是对于半径和最小样本量我们进行取值，然后分析每一个值生成簇得情况，然后根据结果得出最优得半径和样本量。

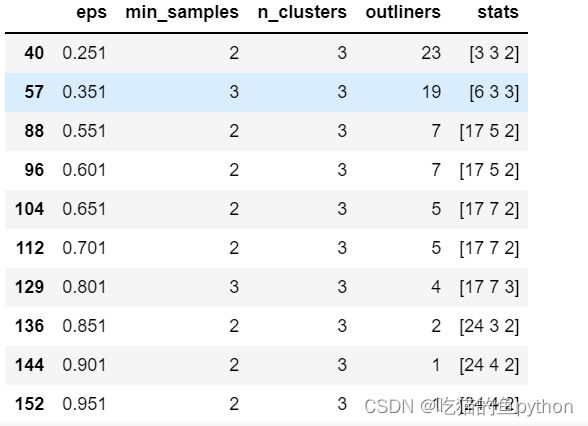
于是我们得到0.801这个半径样本量，最小样本量为3最好。所以我们进行拟合

模型拟合

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

# 利用上述的参数组合值，重建密度聚类算法
dbscan = cluster.DBSCAN(eps = 0.801, min_samples = 3)
# 模型拟合
dbscan.fit(X)
Province['dbscan_label'] = dbscan.labels_
# 绘制聚类聚类的效果散点图
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'dbscan_label', data = Province,
           markers = ['*','d','^','o'], fit_reg = False, legend = False)
# 添加省份标签
for x,y,text in zip(Province.Birth_Rate,Province.Death_Rate, Province.Province):
    plt.text(x+0.1,y-0.1,text, size = 8)
# 添加参考线
plt.hlines(y = 5.8, xmin = Province.Birth_Rate.min(), xmax = Province.Birth_Rate.max(), 
           linestyles = '--', colors = 'red')
plt.vlines(x = 10, ymin = Province.Death_Rate.min(), ymax = Province.Death_Rate.max(), 
           linestyles = '--', colors = 'red')
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
# 显示图形
plt.show()

结果是

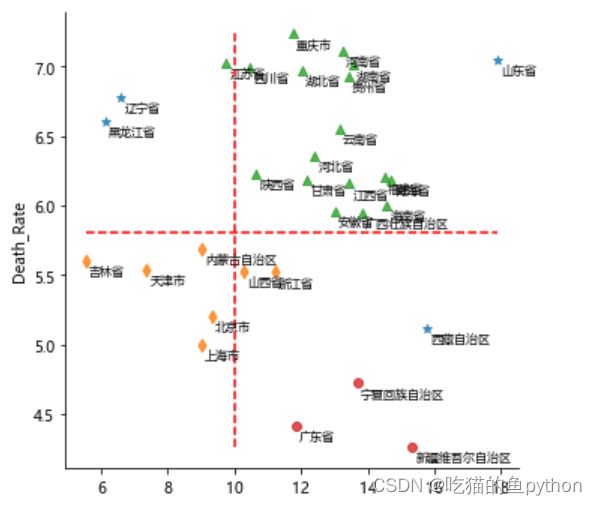
于是我们分析结果，广东，新疆，宁夏这三个地方出生率高，死亡率低，比较适合生存。

文章适合于所有的相关人士进行学习
各位看官看完了之后不要立刻转身呀
期待三连关注小小博主加收藏
小小博主回关快 会给你意想不到的惊喜呀
各位老板动动小手给小弟点赞收藏一下，多多支持是我更新得动力！！！