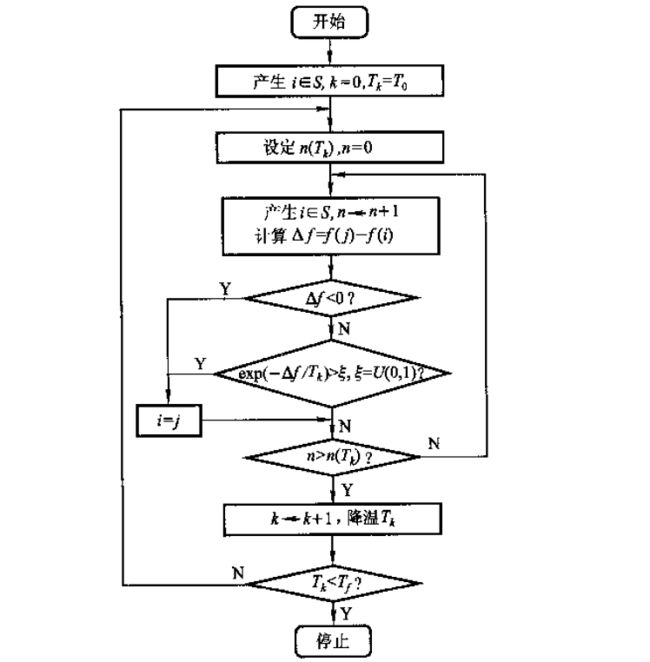
模拟退火算法求解 TSP 问题的代码示例

本文以 TSP 问题为例，通过具体代码，说明模拟退火算法的迭代过程。

模拟退火算法流程图

TSP 问题的代码示例

关于 TSP 问题的介绍从略，算法模块的代码（algorithm.py）如下，注释中已说明算法的迭代过程：

from datetime import datetime
from typing import List
import math
import random


class SimulatedAnnealing(object):
    """
    模拟退火
    """

    def __init__(self, num_point: int, mat_dist: List[List[float]],
                 t_start: int = 5000, t_end: int = 10 ** (-8), coe_anneal: float = 0.98, num_iter: int = 1000):
        """
        模拟退火，数据初始化

        :param num_point:  TSP 节点数量
        :param mat_dist:  距离矩阵
        :param t_start:  初始温度
        :param t_end:  结束温度
        :param coe_anneal:  降温系数
        :param num_iter:  每个温度时的迭代次数
        """

        # 问题参数
        self.num_point = num_point
        self.mat_dist = mat_dist

        # 算法参数
        self.t_start = t_start
        self.t_end = t_end
        self.coe_anneal = coe_anneal
        self.num_iter = num_iter
        print("初始温度： {}".format(self.t_start))
        print("结束温度： {}".format(self.t_end))
        print("降温系数： {}".format(self.coe_anneal))
        print("每个温度时的迭代次数： {}".format(self.num_iter), '\n')

        # 结果
        self.route_opt, self.distance_opt = [], None  # 最优路径、最优路径距离
        self.route_res, self.distance_res = [], None  # 结果路径、结果路径距离

    def run(self):
        """
        算法运行
        :return: 无
        """

        dts = datetime.now()
        random.seed(1024)

        # 初始解
        route = self._init_solution()
        obj = self._get_distance(route=route)
        self.route_opt, self.distance_opt = route, obj

        # loop 1: 降温
        t = self.t_start
        count_anneal = 0
        while t > self.t_end:
            print("当前温度： {}".format(t))
            print("降温次数： {}".format(count_anneal), '\n')

            # loop 2: 每个温度的迭代
            for i in range(self.num_iter):
                route_old = route.copy()
                route = self._create_new_solution(route=route)
                obj, obj_old = self._get_distance(route=route), self._get_distance(route=route_old)
                dis_obj = obj - obj_old
                print("原有路径： {}".format(route_old))
                print("原有路径距离： {}".format(obj_old))
                print("当前路径： {}".format(route))
                print("当前路径距离： {}".format(obj), '\n')

                # Metropolis 准则
                if dis_obj >= 0:
                    r = random.random()
                    if r >= math.exp(-dis_obj / t):
                        route = route_old.copy()
                        print("随机数 {0} 过大，当前路径距离 {1} 较差，恢复原有解".format(r, obj))

                # 更新全局解
                if obj < self.distance_opt:
                    self.route_opt, self.distance_opt = route, obj
                    print("全局最优路径更新为： {}".format(self.route_opt))
                    print("距离： {}".format(self.distance_opt), '\n')

            t *= self.coe_anneal
            count_anneal += 1

        # 运行结果
        self.route_res = route.copy()
        self.distance_res = obj
        print("结果路径： {}".format(self.route_res))
        print("结果路径距离： {}".format(self.distance_res), '\n')

        print("最优路径： {}".format(self.route_opt))
        print("最优路径距离： {}".format(self.distance_opt), '\n')

        dte = datetime.now()
        tm = round((dte - dts).seconds + (dte - dts).microseconds / (10 ** 6), 3)
        print("算法运行时间： {} s".format(tm), '\n')

    def _init_solution(self):
        """
        初始解

        :return: route:  初始路径
        """

        route = [i for i in range(self.num_point)]

        return route

    def _get_distance(self, route: List[int]) -> float:
        """
        计算路径距离
        :param route:  路径
        :return:  距离
        """

        distance = sum(self.mat_dist[route[i]][route[i + 1]] for i in range(len(route) - 1))

        return distance

    def _create_new_solution(self, route: List[int]) -> List[int]:
        """
        产生一个新解
        :param route:  当前解
        :return: route_:  生成的新解
        """

        route_ = route.copy()

        # 通过随机交换两个位置的方式产生新解
        pos1, pos2 = random.randint(0, self.num_point - 1), random.randint(0, self.num_point - 1)
        tmp, route_[pos1] = route_[pos1], route_[pos2]
        route_[pos2] = tmp

        return route_

生成随机算例，并调用算法模块进行求解的主程序代码（main.py）如下：

from datetime import datetime
import math
import random

from algorithm import SimulatedAnnealing


dts = datetime.now()


""" 参数 """

# 地点数量
num_point = 20

# 坐标范围、边界宽度
ran_coo = (0, 100)
edge = 1

# 坐标列表、距离矩阵
random.seed(1024)
list_coo = [(random.randint(ran_coo[0] + edge, ran_coo[1] - edge),
             random.randint(ran_coo[0] + edge, ran_coo[1] - edge)) for _ in range(num_point)]
mat_dist = [[math.sqrt((list_coo[i][0] - list_coo[j][0]) ** 2 + (list_coo[i][1] - list_coo[j][1]) ** 2)
             for j in range(num_point)] for i in range(num_point)]

""" 算法 """

t_start, t_end, coe_anneal, num_iter = 1500, 1000, 0.95, 1000
simulated_annealing = SimulatedAnnealing(num_point=num_point, mat_dist=mat_dist,
                                         t_start=t_start, t_end=t_end, coe_anneal=coe_anneal, num_iter=num_iter)
simulated_annealing.run()


dte = datetime.now()
tm = round((dte - dts).seconds + (dte - dts).microseconds / (10 ** 6), 3)
print("程序运行总时间： {} s".format(tm), '\n')

参考资料

汪定伟《智能优化方法》