数据挖掘期末复习速成大法 华南农业大学
更新日志
[1] 新增了密度聚类峰值的讲解
[2] 新增了 SOM 聚类算法讲解
[3] 修正Apriori规则挖掘二级项集表 到 三级项集表更新策略:新增非频剪枝步骤。
[4] 修正小数定标规范化示例错误
[5] 新增了贝叶斯信念网络的概率计算例题
一文在手,考试无忧
仅代表博主个人观点,大部分是博主个人语言,与任课老师无关,故请勿乱套帽子
跳转到:数据挖掘抱佛脚专用精简版
本速成大法包括:
- 第一部分:重点知识详解
- 第二部分:个人预测考点
课程大纲
- 第1章 绪论
【1】数据挖掘的概念
【2】数据挖掘的研究内容 - 第2章 数据预处理
【1】数据预处理的目的
【2】数据清理
【3】数据集成和数据变换(数据规范化)
【4】数据规约 - 第3章 关联规则挖掘
【1】关联规则挖掘中的基本概念:项,事务,项集,频繁项集,支持度,置信度,最小支持度,最小置信度等
【2】Apriori算法的流程(手算步骤) - 第4章 决策树分类算法
【1】决策树的基本概念:内部节点,叶节点,根节点
【2】基本的决策树生成流程
【3】 ID3算法(流程和计算方法)
【4】 C4.5算法与ID3算法的区别 - 第5章 贝叶斯分类算法
【1】贝叶斯定理和贝叶斯决策准则
【2】朴素贝叶斯分类器(详细计算流程)
【3】贝叶斯信念网络(读懂) - 第6章 人工神经网络算法
【1】人工神经元模型
【2】BP神经网络的原理 - 第7章 支持向量机
【1】支持向量机原理
【2】核函数
【3】支持向量机的优缺点 - 第8,9章 K-means和K-中心点聚类算法
【1】聚类的概念
【2】距离的定义
【3】K-means聚类算法流程
【4】K-means的优点与问题
【5】K-中心点聚类算法
【6】基于密度的聚类算法的原理DBSCAN和密度峰值聚类 - 第10章 SOM神经网络聚类方法
【1】SOM网络的拓扑结构
【2】SOM网络的学习算法
第一章:绪论
1.1 数据挖掘的概念
- 数据挖掘的概念:
把 数量多,不完全,有噪声,模糊的信息 → \rightarrow →我们未知的,有潜在价值,可理解的信息
- 数据挖掘分三个步骤:数据准备,规律寻找,规律表示
所谓“规律表示”,就是数据可视化
1.2 数据挖掘的研究内容
- 数据挖掘最常见的五类知识:广义,关联,分类,预测,偏差
广义知识:就是对于数据上宏观的认知,比如你给出一个商店的盈亏数据,那这堆数据在广义上可能表示了一个现象:这个商店生意很好,那么得出生意很好的这个结论就是我们的广义知识。
关联知识:就是两个对象之间的联系是什么,当然后面我们会知道怎样去对这个联系进行一个量化表示。
预测知识:这里是针对时间序列的数据进行预测,用过往发生的事件未来可能出现的。
偏差知识:研究的是指出数据中的“怪异分子”,异常现象,数据挖掘就是这么一个学科,我们既需要关注大众化的数据堆,也要关注那些少数的异常分子,这就是我们的哲学。
- 数据挖掘的功能:特征化和区分、关联分析、分类预测、聚类、演变分析
特征化:兔子是个怎样的动物?
关联分析::销售啤酒和尿布之间的关系是?
分类预测::某种动物是什么纲目的?预测的话就是:两个小时之后交通量多大?
聚类分析:这群学生里面有几类人?
演变分析:针对时间的种群演化?
数据挖掘的技术举例子:预测技术,关联规则技术,聚类分析技术,人工智能技术,决策树,统计分析,并行计算,可视化技术,进化系统等等。
数据挖掘在生活中的例子:金融领域挺多的,风险评估,效益分析,股市数据预测,医疗也有,药物分子作用的预测和分析,等等。
不用背的,看看就行了
第二章:数据预处理
2.1 数据预处理的目的
为什么我们要进行数据预处理?
因为我们拿到的数据:不完整,有噪声,杂乱模糊。
不完整:就是数据缺失现象
噪声:错误数据混进来了
杂乱模糊:信息重复和冗余,缺乏标准
- 数据预处理技术包括:数据清理,数据集成和变换,数据归约
数据清理:去除噪声和异常
数据集成变换:把数据整合,去除冗余,转化为方便处理的格式(规格化)
数据规约:不影响挖掘结果的前提下,压缩数据,进一步去除冗余,提高挖掘的质量
总的来说,数据清理就是清理,集成就是整合数据,然后变换成我们合适的格式范围,规约就是提高挖掘的质量。
2.2 数据清理
- 对于缺失值的处理:人工补全,或者用unknown表示,用平均值补充,用类似样本的属性补全
- 对于噪声数据的处理:分箱+平滑
分箱技术:分为等宽分箱,等频分箱
宽度:数据区间,频率:数据数量
【1】等宽分箱:先计算这对数据的最大值,最小值,然后算出差值( Δ W \Delta W ΔW)然后根据需求:比如我们需要这堆数据分为多少箱( N N N),再使用
W i d t h = Δ W N Width=\frac{\Delta W}{N} Width=NΔW
求出数据间隔区间(宽度),再归类。
【2】等频分箱,就是:我们先对全部的数据进行排序,我们指出了我们需要分箱的数量: N N N,使用数据的总数 S S S,求出深度:
D e e p t h = S N Deepth = \frac{S}{N} Deepth=NS
平滑处理:无监督的话有三类(平均平滑,边界平滑,中值平滑)
【1】平均平滑:用箱子的数据的平均值替换掉全部数据
【2】边界平滑:箱子里面只有两种数据,一种是最小值一种是最大值,靠近谁就变成谁
【3】中值平滑:用箱子里面的中值替换掉箱子里面的每一个数
例题:某课程成绩score排序后的数据为:61, 66,68,73,77,78,85,88,91。将上述排序的数据划分为等深(深度为3)的箱。
解:
先分箱:(等频分箱,因此需要先排序)
箱1:61, 66, 68
箱2:73, 77, 78
箱3:85, 88, 91
平均平滑:
箱1:65, 65, 65
箱2:76, 76, 76
箱3:88, 88, 88
边界平滑:
箱1:61, 68, 68
箱2:73, 78, 78
箱3:85, 85, 91
对于噪声数据的处理除了:【分箱+平滑】这样的手段以外呢,我们其实还可以使用其余的两种手段:回归法和聚类法。
所谓回归法:就是我们对这些数据进行一个数据规律寻找,得到这个规律之后,然后把不符合这个规律的噪声数据剔除出去。
聚类法和【分箱+平滑】法有异曲同工之妙,先对于数据进行聚类,但是我们就不像分箱一样粗暴地直接按照一维数据的大小进行分箱了,而是以一种向量距离衡量的方式去对数据进行聚类,然后再剔除或者同化那些“异端分子”。
2.3 数据集成和数据变换
做完了数据清理之后,我们整理数据并合并(数据集成的任务),这里的合并,我们理解为:去除冗余和做初步的关系分析。
假如这里的A数据能推导出B数据,那么保留B数据就显得冗余了。我们需要找到两种数据之间的相关性。
- 对于连续域:皮尔逊相关系数R
- 对于离散域:用卡方检验
对于连续域,我们代入两组数据到皮尔逊相关系数公式里面,我们能算出一个相关系数R,这个系数位于区间 [ − 1 , 1 ] [-1,1] [−1,1]之间
- r > 0 r>0 r>0则正相关
- r < 0 r<0 r<0则负相关
- r = 0 r=0 r=0则两组数据相互独立。
同理,卡方检验的原理也类似的,但是最后我们得出的是A和B相关的概率。
一个卡方检验的例子:我们需要统计顾客化妆和性别之间的关系。
| 男 | 女 | 总数 | |
|---|---|---|---|
| 化妆 | 15 | 95 | 110 |
| 不化妆 | 85 | 5 | 90 |
| 总数 | 100 | 100 |
我们先计算期望值:
| 男 | 女 | 总数 | |
|---|---|---|---|
| 化妆 | 15(期望:55) | 95(期望:55) | 110 |
| 不化妆 | 85(期望:45) | 5(期望:45) | 90 |
| 总数 | 100 | 100 |
计算:
x 2 = ( 95 − 55 ) 2 55 + ( 15 − 55 ) 2 55 + ( 85 − 45 ) 2 45 + ( 5 − 45 ) 2 45 = 129.3 x^2 = \frac{(95-55)^2}{55}+\frac{(15-55)^2}{55}+\frac{(85-45)^2}{45}+\frac{(5-45)^2}{45}=129.3 x2=55(95−55)2+55(15−55)2+45(85−45)2+45(5−45)2=129.3
然后计算自由度: V = ( R O W S − 1 ) ∗ ( C O L S − 1 ) = 1 V=(ROWS-1)*(COLS-1)=1 V=(ROWS−1)∗(COLS−1)=1
然后我们查表:
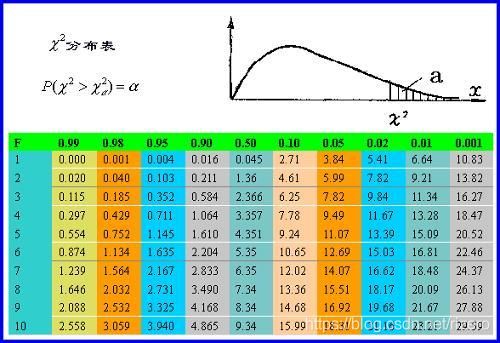
怎么看的表: P ( x 2 > v a l u e ) P(x^2>value) P(x2>value) 的相关概率。
比如这里:因为 129.3 > 10.83 129.3>10.83 129.3>10.83
化妆和性别有99.9%概率相关
我们对数据的相关性寻找之后,然后对数据进行冗余处理,处理完之后,我们就要对数据进行变换操作(规范化)。
常用的手段:
- Min-Max
- Z-score(零均值规范)
- 小数定标
【1】最小最大规范化:

区间映射公式:
K = Δ D n e w Δ D o l d K = \frac{\Delta D_{new}}{\Delta D_{old}} K=ΔDoldΔDnew
V a l u e = K ( v − m i n o l d ) + m i n n e w Value=K(v-min_{old})+min_{new} Value=K(v−minold)+minnew
例题:假定某属性的最小与最大值分别为 8000 元和 14000 元。要将其映射到区间[0.0,1.0]。按照最小-最大规范化方法对属性值进行缩放,则属性值 12600 元将变为?
解:
K = 1 − 0 14000 − 8000 = 1 6000 K=\frac{1-0}{14000-8000}=\frac{1}{6000} K=14000−80001−0=60001
( 12600 − 8000 ) ∗ K + 0 = 0.767 (12600-8000)*K+0=0.767 (12600−8000)∗K+0=0.767
【2】零均值规范化:
我们利用均值和标准差对于区间进行映射。
公式: V a l u e = V a l u e − v 均 值 v 标 准 差 Value=\frac{Value-v_{均值}}{v_{标准差}} Value=v标准差Value−v均值
标准差的计算方法:
∑ ( x i − x ˉ ) 2 n \sqrt{\sum{\frac{(x_i-\bar{x})^2}{n}}} ∑n(xi−xˉ)2
注意有时候不一定会用标准差,可能是:均值绝对偏差。
例题:假定属性平均家庭月总收入的均值和标准差分别为 9000 元和 2400 元,值10600 元使用 z-score 规范化转换为?
解:
( 10600 − 9000 ) / 2400 = 1.5 (10600-9000)/2400=1.5 (10600−9000)/2400=1.5
【3】小数定标法:
就是人为放缩10的倍数,并且保证:最大的数小于1,注意,不能等于1。
比如:有一组数据: [ 900 , 1000 ] [900,1000] [900,1000],那么我们用10000进行放缩,那么得到的新区间就是 [ 0.09 , 0.1 ] [0.09,0.1] [0.09,0.1]
比如:有一组数据: [ 900 , 999 ] [900,999] [900,999],那么我们用1000进行放缩,那么得到的新区间就是 [ 0.9 , 0.999 ] [0.9,0.999] [0.9,0.999]
2.3 数据规约
这里不是重点,常用的数据规约方法:立方体聚集,维规约,数据压缩,值规约,数据离散化等…
第三章 关联规则挖掘
所谓关联规则挖掘就是发现数据项集之间的关联关系。
关联规则研究的是:集合之间关系。
3.1 基本概念
- 项:最小的信息单位
- 项集:多个项的集合(这是我们研究规则的单位)
- 频繁项集:不小于最小支持度的项集
- 规则:项集之间出现的因果关系。比如: X ⇒ Y X\Rightarrow Y X⇒Y,当 X X X项集的项出现的时候, Y Y Y项集的项也出现。
- 事务:多个项集组成事务
- 支持度: P s u p = P ( A & B ) P_{sup}=P(A\&B) Psup=P(A&B)
- 置信度:针对某个事务的置信度,比如: A → B : c o n f = P s u p P ( A ) {A\rightarrow B}:conf=\frac{P_{sup}}{P(A)} A→B:conf=P(A)Psup
- 最小支持度:人为设定的,用于筛选项集
- 最小置信度:人为设定的,用于筛选规则
- 强关联规则:满足大于最小事务置信度的规则
3.2 Apriori算法的流程(掌握手算步骤)
例题1:下面是一个数据库的事务列表,在数据库中有9笔交易。每笔交易都用唯一的标识符TID作标记,交易中的项按字典序存放,用Apriori算法寻找频繁项集。设最小支持度计数为2,即min_ sup=2。
| 事务 | 包含的项集 |
|---|---|
| T100 | I1,I2,I5 |
| T200 | I2,I4 |
| T300 | I2,I3 |
| T400 | I1,I2,I4 |
| T500 | I1,I3 |
| T600 | I2,I3 |
| T700 | I1,I3 |
| T800 | I1,I2,I3,I5 |
| T900 | I1,I2,I3 |
解:
如果给的是最小支持度,那么可以根据公式还原出最小支持数:
P m i n _ s u p = m i n _ s u p S u m 事 务 P_{min\_sup}=\frac{min\_sup}{Sum_{事务}} Pmin_sup=Sum事务min_sup
比如这里的最小支持度就是2/9=22.2%
现在题目已经给出我们的最小支持数了,就无需我们去算了。
这里的最小支持度计数=2的意思是,我们只保留出现次数大于2的项集子集。
首先,根据单项项集开始:
表1:(一级频繁项集表)
| 项集 | 出现次数 |
|---|---|
| I 1 I_1 I1 | 6 |
| I 2 I_2 I2 | 7 |
| I 3 I_3 I3 | 6 |
| I 4 I_4 I4 | 2 |
| I 5 I_5 I5 | 2 |
只要大于等于2的都留下,那好,大家都都留下了。
我们继续,拓展项数=2的项集。
| 项集 | 出现次数 |
|---|---|
| I 1 , I 2 I_1,I_2 I1,I2 | 4 |
| I 1 , I 3 I_1,I_3 I1,I3 | 4 |
| I 1 , I 4 I_1,I_4 I1,I4 | 1 |
| I 1 , I 5 I_1,I_5 I1,I5 | 2 |
| I 2 , I 3 I_2,I_3 I2,I3 | 4 |
| I 2 , I 4 I_2,I_4 I2,I4 | 2 |
| I 2 , I 5 I_2,I_5 I2,I5 | 2 |
| I 3 , I 4 I_3,I_4 I3,I4 | 0 |
| I 3 , I 5 I_3,I_5 I3,I5 | 1 |
| I 4 , I 5 I_4,I_5 I4,I5 | 0 |
我们把不满足最小支持数的剔除出去,剩下:
表2:(二级频繁项集表)
| 项集 | 出现次数 |
|---|---|
| I 1 , I 2 I_1,I_2 I1,I2 | 4 |
| I 1 , I 3 I_1,I_3 I1,I3 | 4 |
| I 1 , I 5 I_1,I_5 I1,I5 | 2 |
| I 2 , I 3 I_2,I_3 I2,I3 | 4 |
| I 2 , I 4 I_2,I_4 I2,I4 | 2 |
| I 2 , I 5 I_2,I_5 I2,I5 | 2 |
好了,继续,我们研究项数=3的:
| 项集 | 出现次数 |
|---|---|
| I 1 , I 2 , I 3 I_1,I_2,I_3 I1,I2,I3 | 2 |
| I 1 , I 2 , I 4 I_1,I_2,I_4 I1,I2,I4 | 1 |
| I 1 , I 2 , I 5 I_1,I_2,I_5 I1,I2,I5 | 2 |
| I 1 , I 3 , I 4 I_1,I_3,I_4 I1,I3,I4 | 0 |
| I 1 , I 3 , I 5 I_1,I_3,I_5 I1,I3,I5 | 0 |
| I 1 , I 4 , I 5 I_1,I_4,I_5 I1,I4,I5 | 0 |
| I 2 , I 3 , I 4 I_2,I_3,I_4 I2,I3,I4 | 0 |
| I 2 , I 3 , I 5 I_2,I_3,I_5 I2,I3,I5 | 1 |
| I 3 , I 4 , I 5 I_3,I_4,I_5 I3,I4,I5 | 0 |
根据最小支持数=2,我们剔除掉,剩下:
| 项集 | 出现次数 |
|---|---|
| I 1 , I 2 , I 3 I_1,I_2,I_3 I1,I2,I3 | 2 |
| I 1 , I 2 , I 5 I_1,I_2,I_5 I1,I2,I5 | 2 |
一级频繁项集是:(见表1)
二级频繁项集是:(见表2)
三级频繁项集是: { I 1 , I 2 , I 5 } \{I_1,I_2,I_5\} {I1,I2,I5}, { I 1 , I 2 , I 3 } \{I_1,I_2,I_3\} {I1,I2,I3}
利用频繁项集,我们就能假设出一堆关联规则了。
计算关联规则的例子看下面,因为上面的例子太多规则了,算死人。
例题2:如下表,我们的最小支持数是2,找出所有的关联规则并计算置信度。
| TID | 包含 |
|---|---|
| 001 | M,S,E |
| 002 | M,T,P |
| 003 | M,T,P,S |
| 004 | T,P |
解:
一级表:
| 一级项集 | 出现次数 |
|---|---|
| M | 3 |
| E | 1 |
| T | 3 |
| P | 3 |
| S | 2 |
因此,一级频繁项集表:( m i n _ s u p = 2 min\_sup=2 min_sup=2)
| 一级频繁项集 | 出现次数 |
|---|---|
| M | 3 |
| T | 3 |
| P | 3 |
| S | 2 |
二级的项集表:
| 二级项集 | 出现次数 |
|---|---|
| M,T | 2 |
| M,P | 2 |
| M,S | 2 |
| T,P | 3 |
| T,S | 1 |
| P,S | 1 |
因此,得到二级频繁项集表:
| 二级频繁项集 | 出现次数 |
|---|---|
| M,T | 2 |
| M,P | 2 |
| M,S | 2 |
| T,P | 3 |
继续,我们得到三级项集表:
| 三级项集 | 出现次数 |
|---|---|
| M,T,P | 2 |
| M,T,S | 1 |
| M,P,S | 1 |
得到三级频繁项集表:
| 三级频繁项集 | 出现次数 |
|---|---|
| M,T,P | 2 |
我们的频繁项集:{ M M M},{ T T T},{ P P P},{ S S S},{ M , T M,T M,T},{ M , P M,P M,P},{ M , S M,S M,S},{ T , P T,P T,P},{ M , T , P M,T,P M,T,P}
整合所有的频繁项集:
| 项集标记 | 频繁项集 | 出现次数 |
|---|---|---|
| 1 | M,T,P | 2 |
| 2 | M,T | 2 |
| 3 | M,P | 2 |
| 4 | M,S | 2 |
| 5 | T,P | 3 |
| 6 | M | 3 |
| 7 | T | 3 |
| 8 | P | 3 |
| 9 | S | 2 |
然后找出之间的子集关系:
1的子集是:5,6,7,8,2,3
2的子集是:6,7
3的子集是:6,8
4的子集是:6,9
5的子集是:7,8
因此我们可以讨论出很多的关联规则来,需要注意的是:只有非存在交集关系的项集之间才能讨论规则。
(我们就不全部规则列出来了,太多了)
单单以项集1的子集为例进行讨论找出一些形如【二级项集和一级项集】的规则。
根据上面的子集关系,我们发现非存在交集关系的有【二级项集和一级项集】之间:5和6,7和3,8和2
我们得到的部分关联规则:
置信度的计算( A ∈ C , B ∈ C , A ∩ B = ∅ A\in C,B\in C,A\cap B=\emptyset A∈C,B∈C,A∩B=∅,,规则 A → B A\rightarrow B A→B):
c o n f = C 的 次 数 A 的 次 数 conf =\frac{C的次数}{A的次数} conf=A的次数C的次数
因此,我们不难知道下面的置信度的分子全部是2,因为他们同属一个母集1,母集1的出现次数是2,而且这些集合之间不存在交集关系。
我们得到在母集1下面的置信度表:
| 关联规则 | 置信度 |
|---|---|
| 6 → 5 6\rightarrow5 6→5 | 2/3 |
| 5 → 6 5\rightarrow6 5→6 | 2/3 |
| 7 → 3 7\rightarrow3 7→3 | 2/3 |
| 3 → 7 3\rightarrow7 3→7 | 2/2 |
| 8 → 2 8\rightarrow2 8→2 | 2/3 |
| 2 → 8 2\rightarrow8 2→8 | 2/2 |
接下来,我们需要计算2,3,4,5的置信度表,这里就不演示了。
我们把整个流程梳理一遍:
- 利用最小支持数逐步筛选出多级频繁项集,得到频繁项集表
- 找出子集关系
- 构造非交集子集之间的规则表,
- 计算置信度,得到多个置信度表
- 对每一个置信度表用最小置信度进行筛选
上面我们演示的是针对单维离散化的数据进行规则挖掘,如何对多维连续的数据进行挖掘呢?
看下面例题:
例题:所示关系表 People 是要挖掘的数据集,有三个属性(Age,Married,NumCars)假如用户指定的最小支持度40%,最小置信度50% ,试挖掘表 2 中的数量关联规则
| TID | Age | Married | NumCars |
|---|---|---|---|
| 001 | 23 | F | 0 |
| 002 | 25 | T | 1 |
| 003 | 29 | F | 1 |
| 004 | 34 | T | 2 |
| 005 | 38 | T | 2 |
解:
首先,对连续数据进行离散化:
| Age | AID |
|---|---|
| 20-24 | A1 |
| 25-29 | A2 |
| 大于等于30 | A3 |
因此我们得到新的表格:
| TID | Age | Married | NumCars |
|---|---|---|---|
| 001 | A1 | F | 0 |
| 002 | A2 | T | 1 |
| 003 | A2 | F | 1 |
| 004 | A3 | T | 2 |
| 005 | A3 | T | 2 |
然后针对各个维度进行寻找频繁项集,列出我们三个频繁项集表:
我们的最小支持度是40%,我们这里有5个数据,因此我们的最小支持数是2
Age 的一级频繁项集表:
| 项集 | 出现次数 |
|---|---|
| A{2} | 2 |
| A{3} | 2 |
Married 的一级频繁项集表:
| 项集 | 出现次数 |
|---|---|
| M{T} | 3 |
| M{F} | 2 |
Numcars 的一级频繁项集表:
| 项集 | 出现次数 |
|---|---|
| N{1} | 2 |
| N{2} | 2 |
整合之后的二级项集表:
| 项集 | 出现次数 |
|---|---|
| A{2}M{T} | 1 |
| A{2}M{F} | 1 |
| A{2}N{1} | 2 |
| A{2}N{2} | 0 |
| A{3}M{T} | 2 |
| A{3}M{F} | 0 |
| A{3}N{1} | 0 |
| A{3}N{2} | 2 |
| M{T}N{1} | 1 |
| M{T}N{2} | 2 |
| M{F}N{1} | 1 |
| M{F}N{2} | 0 |
得到二级频繁项集表:
| 项集 | 出现次数 |
|---|---|
| A{2}N{1} | 2 |
| A{3}M{T} | 2 |
| A{3}N{2} | 2 |
| M{T}N{2} | 2 |
整合出三级项集表:
| 项集 | 出现次数 |
|---|---|
| A{2}M{T}N{1} | 1 |
| A{3}M{T}N{1} | 0 |
| A{3}M{T}N{2} | 2 |
| A{2}M{T}N{2} | 0 |
筛选出三级频繁项集表:
| 项集 | 出现次数 |
|---|---|
| A{3}M{T}N{2} | 2 |
整理出频繁项集表:
| 项集ID | 项集 | 出现次数 |
|---|---|---|
| 1 | A{2} | 2 |
| 2 | A{3} | 2 |
| 3 | M{T} | 3 |
| 4 | M{F} | 2 |
| 5 | N{1} | 2 |
| 6 | N{2} | 2 |
| 7 | A{2}N{1} | 2 |
| 8 | A{3}M{T} | 2 |
| 9 | A{3}N{2} | 2 |
| 10 | M{T}N{2} | 2 |
| 11 | A{3}M{T}N{2} | 2 |
11的子集:【2,3,6】,【8,9,10】
10的子集:3,6
9的子集:2,6
8的子集:2,6
7的子集:1,5
我们先看11的子集:满足可以构成规则(【一级项集和二级项集】)的有:2和10
看10的子集,满足构成规则的有:3和6
看9的子集:2和6
看8的子集:2和6,重复了
看7的子集:1和5
整合规则表:
| 规则 | 置信度 |
|---|---|
| 2 → 10 2\rightarrow 10 2→10 | 2/2=100% |
| 10 → 2 10\rightarrow 2 10→2 | 2/2=100% |
| 3 → 6 3\rightarrow 6 3→6 | 2/3=67% |
| 6 → 3 6\rightarrow 3 6→3 | 2/2=100% |
| 5 → 1 5\rightarrow 1 5→1 | 2/2=100% |
| 1 → 5 1\rightarrow 5 1→5 | 2/2=100% |
补充修正:
根据上面的方法,我们的步骤:
最小支持度找一级频繁项集表 → \rightarrow →最小支持度找二级频繁项集表 → \rightarrow →最小支持度找三级频繁项集表 → \rightarrow →整理所有的频繁项集表 → \rightarrow →子集分析 → \rightarrow →规则生成 → \rightarrow →计算规则置信度
在这里,需要注意的,根据课本的描述,我们再从低级频繁项集表到高级的项集表的时候,需要进行:非包含频繁项集元素剪枝的操作。
但如果真做题的时候剪枝操作会导致可能出现脑子混乱,因此,我们可以在找出更高一级的频繁项集表之后,检查一下,是否满足条件就行了。
第四章 决策树分类算法
决策树包含三类节点:内部节点,叶节点,根节点
基本的决策树生成流程分为两个步骤:决策树生成和决策树修剪。
决策树生成: 根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则停止决策树停止生长。
剪枝:决策树容易过拟合,一般来需要剪枝,缩小树结构规模、缓解过拟合。
下面是ID3算法的伪代码:
(算法伪代码需要记住!)
def Gen_tree(samples, at_list):
N = Node() # 创建结点N
if samples all in same_Class:
return N # 如果samples都在同一个类C 则返回N作为叶结点,以类C标记,程序结束
if at_list.size == None:
return N #如果attribute_list为空,则返回N作为叶结点,标记为samples中最普通的类
test_at = max_info(at_list) # 选择at_list中具有最高信息增益的属性test_at;
N = test_at # 标记结点N为test_attribute
for vi in test_at.options:
N.branch(condition = 'test_at=vi').grow()
# 对于test_at中的每一个已知值vi,由结点N生长出一个条件为test_at=ai的分枝
si = find_from_samples(samples, test_at = vi)#设si是samples中test_attribute=ai的样本的集合,如果 si为空则加上一个树叶,标记为samples中最普通的类,否则加上一个由Gen_tree(si,at_list)返回的结点
if si == None:
N.branch(condition = 'test_at=vi').end()
else:
Gen_tree(si, at_list.remove(test_at))
事实上,我们生成的决策树不是唯一的,衡量一个决策树的好坏,我们一般:树越小,预测能力越强。
但是构造最小的树是NP难问题。
什么是信息增益?
例如,知道“期中考试是否及格”,可能会使得“期末考试是否及格”的不确定性变小,即熵减少,即产生了信息增益。
ID3的优点就是简单。ID3算法的核心是在决策树各级结点上选择属性时,用信息增益作为属性的选择标准
缺点:
- 【1】信息增益计算依赖于特征数目较多的特征,而属性取值最多的属性并不一定最优
- 【2】分枝节点上只考虑了单个属性
- 【3】抗噪差
- 【4】仅可处理离散属性
ID3的改进版本:C4.5算法
区别是分支指标使用了增益比例,而不是直接使用信息增益。
选择取值较集中的属性(即熵值最小的属性)。
我们怎样评估一棵决策树呢?
可以使用K交叉验证:我们把学习-验证(用独立的测试样本)的过程重复k次,称为k次迭代,然后选择精度最高的那棵树。
怎样解决决策树的过拟合问题呢?
两种方法: 先剪枝,后剪枝。
所谓剪枝,就是限制决策树的高度和叶子结点处样本的数目
第五章 贝叶斯分类算法
这一章必考一道计算。
5.1 朴素贝叶斯分类
P ( A ∣ B ) P(A|B) P(A∣B) = SUM(AB) / SUM(B)
记住贝叶斯概决策公式:
V = a r g m a x l a b e l ∈ l a b e l s ( P ( L a b e l ) P ( C 1 ∣ L a b e l ) P ( C 2 ∣ L a b e l ) . . . P ( C n ∣ L a b e l ) ) V=argmax_{label\in labels}(P(Label)P(C_1|Label)P(C_2|Label)...P(C_n|Label)) V=argmaxlabel∈labels(P(Label)P(C1∣Label)P(C2∣Label)...P(Cn∣Label))
直接上例题:已知
| day | outlook | temperature | humidity | wind | Playtennis |
|---|---|---|---|---|---|
| 1 | sunny | hot | high | weak | no |
| 2 | sunny | hot | high | strong | no |
| 3 | overcast | hot | high | weak | yes |
| 4 | rain | mild | high | weak | yes |
| 5 | rain | cool | normal | weak | yes |
| 6 | rain | cool | normal | strong | no |
| 7 | overcast | cool | normal | strong | yes |
| 8 | sunny | mild | high | weak | no |
| 9 | sunny | cool | normal | weak | yes |
| 10 | rain | mild | normal | weak | yes |
| 11 | sunny | mild | normal | strong | yes |
| 12 | overcast | mild | high | strong | yes |
| 13 | overcast | hot | normal | weak | yes |
| 14 | rain | mild | high | strong | no |
问当出现:
问这一天是否适合于打网球?
解:
为了方便数出来,我整理了只有yes情况的表:
| day | outlook | temperature | humidity | wind | Playtennis |
|---|---|---|---|---|---|
| 3 | overcast | hot | high | weak | yes |
| 4 | rain | mild | high | weak | yes |
| 5 | rain | cool | normal | weak | yes |
| 7 | overcast | cool | normal | strong | yes |
| 9 | sunny | cool | normal | weak | yes |
| 10 | rain | mild | normal | weak | yes |
| 11 | sunny | mild | normal | strong | yes |
| 12 | overcast | mild | high | strong | yes |
| 13 | overcast | hot | normal | weak | yes |
- P ( s u n n y ∣ y e s ) = S U M ( s u n n y & y e s ) / S U M ( y e s ) = 2 9 P(sunny|yes)=SUM(sunny \& yes)/ SUM(yes) = \frac{2}{9} P(sunny∣yes)=SUM(sunny&yes)/SUM(yes)=92
- P ( c o o l ∣ y e s ) = S U M ( c o o l & y e s ) / S U M ( y e s ) = 3 9 P(cool|yes)=SUM(cool \& yes)/ SUM(yes) =\frac{3}{9} P(cool∣yes)=SUM(cool&yes)/SUM(yes)=93
- P ( h i g h ∣ y e s ) = S U M ( h i g h & y e s ) / S U M ( y e s ) = 3 9 P(high|yes)=SUM(high \& yes)/ SUM(yes)=\frac{3}{9} P(high∣yes)=SUM(high&yes)/SUM(yes)=93
- P ( s t r o n g ∣ y e s ) = S U M ( s t r o n g & y e s ) / S U M ( y e s ) = 3 9 P(strong|yes)=SUM(strong \& yes)/ SUM(yes)=\frac{3}{9} P(strong∣yes)=SUM(strong&yes)/SUM(yes)=93
- P ( y e s ) = 9 14 P(yes)=\frac{9}{14} P(yes)=149
得出yes的情况:
9 14 ∗ 1 4 ∗ 3 9 ∗ 3 9 ∗ 3 9 = 0.005291 \frac{9}{14}*\frac{1}{4}*\frac{3}{9}*\frac{3}{9}*\frac{3}{9}=0.005291 149∗41∗93∗93∗93=0.005291
同理,算出no的情况:
0.0205704 0.0205704 0.0205704
因此,更大的可能是不能出去玩。
5.2 贝叶斯定理和贝叶斯决策准则
上面例题实际上我们利用贝叶斯概率公式也是可以计算的,但过于复杂,我们写代码算会更加方便:参见我的另一篇文章:朴素贝叶斯分类器Numpy实现【原创代码】。
贝叶斯定理(贝叶斯概率公式):
P ( l a b e l ∣ < c 1 , c 2 , c 3 . . . c n > ) = P ( l a b e l ) P ( c 1 ∣ l a b e l ) P ( c 2 ∣ l a b e l ) P ( c 3 ∣ l a b e l ) . . . P ( c n ∣ l a b e l ) P ( c 1 ) P ( c 2 ) P ( c 3 ) . . . P ( c n ) P(label|
- 先验概率:P(A)通常在试验之前已知,因此习惯上称为先验概率。
- 后验概率:P(B|A)反映了A发生之后,事件B发生的可能性大小,通常称之为后验概率
贝叶斯决策准则:如果对于任意 j j j,都有 P ( C i ∣ X ) > P ( C j ∣ X ) P(C_i|X)>P(C_j|X) P(Ci∣X)>P(Cj∣X)成立,则样本模式X被判定为类别。
贝叶斯算法的优点:
- 逻辑简单、易于实现、
- 时间空间开销小;
- 稳定,健壮(不会因为数据之间的特点差异大而导致结果很离谱)
贝叶斯算法的缺点:缺点是属性间类条件独立的这个假定,而很多实际问题中这个独立性假设并不成立,如果在属性间存在相关性的实际问题中忽视这一点,会导致分类效果下降
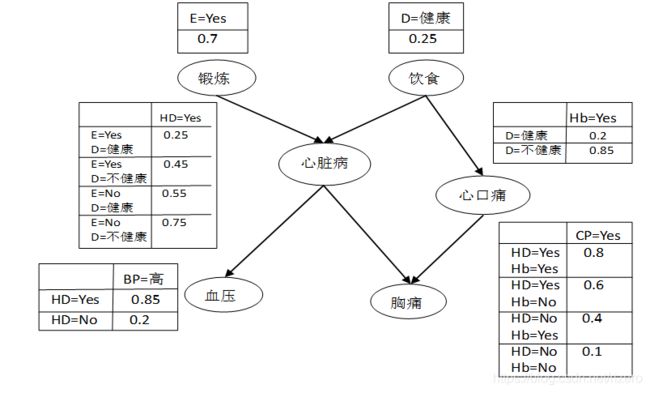
贝叶斯信念网络:简称BBN,用图形表示一组随机变量之间的概率关系,有向无环图+一张概率表。
例题:贝叶斯信念网络计算例题:(可能会考的)
解:
能推导出心脏病的无非就是:锻炼事件和饮食事件,
P ( H D = y e s ) P(HD = yes) P(HD=yes) = 0.25 ∗ 0.7 ∗ 0.25 + 0.45 ∗ 0.7 ∗ 0.75 + 0.55 ∗ 0.3 ∗ 0.25 + 0.75 ∗ 0.3 ∗ 0.75 =0.25*0.7*0.25+0.45*0.7*0.75+0.55*0.3*0.25+0.75*0.3*0.75 =0.25∗0.7∗0.25+0.45∗0.7∗0.75+0.55∗0.3∗0.25+0.75∗0.3∗0.75
= 0.49 =0.49 =0.49
(2)已知有高血压,问得心脏病的概率?
P ( B P = h i g h ) = P(BP=high)= P(BP=high)=
P ( H D = y e s ∣ B P = h i g h ) = P ( H D = y e s & B P = h i g h ) ∗ P ( H D = y e s ) P ( B P = h i g h ) P(HD=yes|BP=high)=\frac{P(HD=yes \& BP=high)*P(HD=yes)}{P(BP=high)} P(HD=yes∣BP=high)=P(BP=high)P(HD=yes&BP=high)∗P(HD=yes)
= 0.85 ∗ 0.49 0.5185 =\frac{0.85*0.49}{0.5185} =0.51850.85∗0.49
第六章 人工神经网络算法
6.1 人工神经元(MP模型)
是一个多输入,单输出的非线性部件
公式:
y i = f ( ∑ w i x i − θ ) y_i = f(\sum w_ix_i-\theta) yi=f(∑wixi−θ)
- θ \theta θ 叫做神经元的阈值
- w i w_i wi 叫做神经元的权重
- x i x_i xi 是神经元的输入信号
- f ( ) f() f()我们叫做激活函数
激活函数大家都不陌生了,sigmoid也是常用的,对于MP模型,最经典的是阶跃函数。

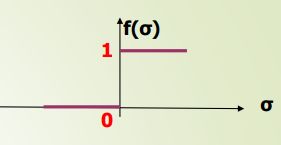
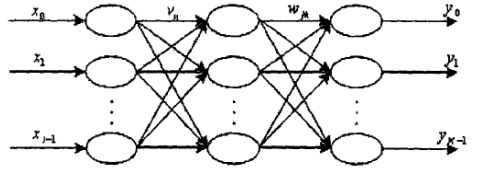
6.2 BP 神经网络
BP神经网络全称就是误差后向传播网络。是属于前馈网络之一。
BP用的激活函数需要处处可微,因此不能直接使用像MP模型那种激活函数
误差反向传播阶段(就是我们的权重修正阶段)
学习率在计算新的权重的时候使用
Delta学习规则又称梯度法,其要点是改变单元间的连接权重来减小系统实际输出与期望输出间的误差。(BP神经网络的原理)
第七章 支持向量机
SVM是基于统计学习理论和结构风险最小原理的机器学习算法
核函数的分类:
- 线性核函数:
- 多项式核函数
- Sigmoid核函数
- Gauss径向基核函数
不同的核函数所产生的性能是不同的,建立支持向量机的核函数必须满足Mercer定理条件。
SVM的优点:
- 用内积核函数代替向高维空间的非线性映射
- 对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想是SVM方法的核心
- 避免了维数灾难
- 小样本学习方法
SVM的缺点:
- 多分类问题:经典的支持向量机算法只给出了二类分类的算法,而在实际应用中,解决多类分类问题。可通过多个二类支持向量机的组合来解决。主要有一对多、一对一和SVM决策树;再就是通过构造多个分类器的组合来解决
- SVM算法对大规模训练样本难以实施
第八章 聚类算法
无非就是两类:K-means 和 K-中心点,要求能手算第一轮的迭代。
聚类:将未知类别的样本集划分为若干簇的过程
8.1 距离函数
所谓距离就是我们用来衡量两个向量之间的相似性。
欧氏距离: d i s t ( X , Y ) = ∑ ( x i − y i ) 2 dist(X,Y)=\sqrt{\sum(x_i-y_i)^2} dist(X,Y)=∑(xi−yi)2
曼哈顿距离: d i s t ( X , Y ) = ∑ ( ∣ x i − y i ∣ ) dist(X,Y)=\sum(|x_i-y_i|) dist(X,Y)=∑(∣xi−yi∣)
余弦距离: c o s ϕ = a ⃗ ∙ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos\phi = \frac{\vec{a}\bullet \vec{b}}{|\vec{a}|| \vec{b}|} cosϕ=∣a∣∣b∣a∙b
仔细观察,欧氏距离是闵可夫斯基距离的一种特殊形式
8.2 K-means算法实现
算法步骤:
1、随机选取K个质心的值
2、计算各个点到质心的距离
3、将点的类划分为离他最近的质心,形成K个cluster
4、根据分类好的cluster,在每个cluster内重新计算质心(平均每个点的值)
5、重复迭代2-4步直到满足迭代次数或误差小于指定的值
例题:给定以下数据集{5, 6, 3, 22, 17 ,2, 24},进行K-Means聚类,设定聚类数K为2个,初始聚类中心为2和6,相似度按照欧式距离计算。要求写出具体步骤
解:
第一次迭代:
| 点 | 距离M1=2的距离 | 距离M2=6的距离 | 属于的类 |
|---|---|---|---|
| 5 | 3 | 1 | M2 |
| 6 | 4 | 0 | M2 |
| 3 | 1 | 3 | M1 |
| 22 | 20 | 16 | M2 |
| 17 | 15 | 11 | M2 |
| 2 | 0 | 4 | M1 |
| 24 | 22 | 18 | M2 |
M1:3,2
M2:5,6,22,17,24
更新之后的中心点:M1 = 2.5,M2=14.8
…
Kmeans的优点和缺点:
优点:
- 简单、快速,复杂度: O ( n k t ) O(nkt) O(nkt),t是迭代次数,n是样本数量,k是中心数
- 簇与簇区别明显时的效果好
缺点:
- 聚类个数k依赖于用户参数的指定
- 基于距离的聚类算法只能发现球状簇,很难发现其他形状的簇
- 初始中心随机选取,导致结果波动较大,稳定性较差。
我们如何去确定K值?
使用手肘法
我们设定损失函数的计算方法:
S S E = ∑ ( ∑ ∣ p − m i ∣ 2 ) SSE=\sum(\sum|p-m_i|^2) SSE=∑(∑∣p−mi∣2)
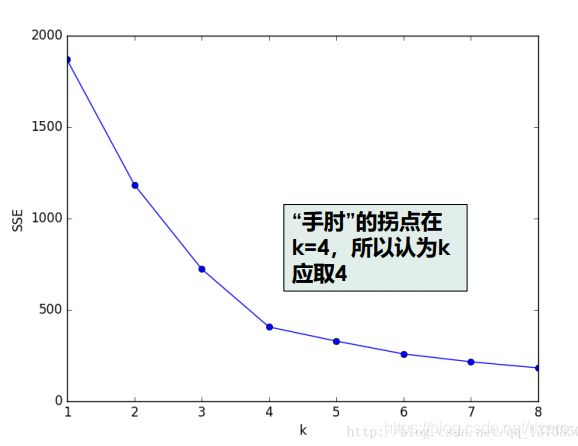
8.2 K-中心点算法实现
K中心点主要解决Kmeans算法的:离群点干扰问题
K中心点算法选择曼哈顿距离
下面描述的K中心点算法和我之前的博客有部分出入,请以下面的为准
算法步骤:
1、随机选取K个质心的值 (质心必须是某些样本点的值,而不是任意值)
2、计算各个点到质心的距离
3、将点的类划分为离他最近的质心,形成K个cluster
4、根据分类好的cluster,在每个cluster内重新计算质心(我们获取的质心永远是样本之一):
-
4.1 计算cluster内非中心点样本点到当前中心点交换之后,得到多个交换方案和每个方案的代价(计算方式参照下面例题)
-
4.2 采取代价最小的点交换方案
5、重复迭代2-4步直到满足迭代次数或误差小于指定的值
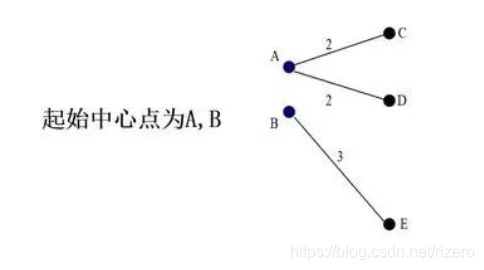
例题:假如空间中的五个点{A、B、C、D、E}如下图所示,各点之间的距离关系如下表所示,根据所给的数据对其运行K-中心点聚类算法实现划分聚类(设K=2)
解:实际上是很简单的,不过任课老师给的PPT实在是晦涩难懂,下面讲人话把他讲通:
第二步:交换中心点,更新策略
怎么交换呢?
我们用不是中心点的{DCE}和{AB}做交换。
因此,我们有如下新的中心点策略:
- {A,C}
- {A,D}
- {A,E}
- {B,C}
- {B,D}
- {B,E}
根据新的策略,我们再聚类一次:

我们再计算每一种策略的损失:
- {A,C}:5
- {A,D}:5
- {A,E}:5
- {B,C}:5
- {B,D}:5
- {B,E}:6
(PPT上面说的一大堆废话,距离的衡量就这么简单,PPT上的那些-2是怎么计算出来的?减7就是了)
可见,下一次的更新,我们可以有很多的选择,一般来说,我们选择最先遇到的,那就是{AC}策略。
以上是第一次迭代的情况。我们迭代到代价不再减少为止就能停止了。
8.3 密度聚类算法
我们看到Kmeans和K中心点的聚类只能聚类球形簇,什么叫做球簇呢?,像下面:
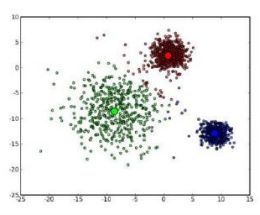
但是万一哈,遇到你看像下面这种类我们用K类的法聚就很难了:

所以,我们需要一种能聚出上面这种奇怪形状的类的算法,因此就有了我们的密度聚类算法。
下面用人话讲通密度聚类算法DBSCAN。
首先,我们先定义一下下面的量。
- 密度:是对于某个点而言的,以某个点作为中心,然后以一定的距离范围画一个圈,然后统计在这个圈里面的数据点的数量,这个数量我们称呼为密度。
- 截断距离:就是我们上述的距离范围
- 阈值距离:在截断范围里面,我们有很多点,我们需要对这些点分为两类,一类是距离中心点近的,一类的距离中心点远的。这个分界就是阈值距离。
不懂?看下面这个图。R就是截断距离,r是阈值距离。红色的点,我们叫做低密度点,黄色的点,我们叫做高密度的点。

然后,我们对高密度点进行一次,遍历,利用同样的方式,进行划分阈值距离和截断距离:
- 是源中心点的高密度点,也是当前中心点的高密度点。那么我们把这两个点相连,我们叫他【双高点】
- 虽然原来是源中心点的高密度点,但是是当前中心点的低密度点,那么我们把这个点连到距离他最近的【双高点】。这种点我们叫做边界点。
如此下去,我们就会出现一个类簇。
但是,我们会有这样一个问题,我们的分类的标准变成了:只有满足固定密度的点,我们才能聚成类。
万一不同类的密度不一样呢?所以,这个是密度聚类的一个改进点的思考。
PPT上描述了一些概念,考试记一下:
【1】局部密度:
ρ i = ∑ x ( d ) \rho_i = \sum x(d) ρi=∑x(d)
x ( d ) = { 1 , d < R 0 , d > = R x(d) =\begin{cases}1,d
- d就是中心点周围某一个点到他之间的距离。
- R就是截断距离。
所谓密度,就是满足距离范围内点的数量。
【2】距离:
这个就是上述的阈值距离r。
θ i = min j : ρ j > ρ i ( d i j ) \theta_i = \min_{j:\rho_j>\rho_i}(d_ij) θi=j:ρj>ρimin(dij)
用来区分哪些是高密度点,哪些是低密度点。
【3】聚类中心:
具有大局部密度而且同时拥有大阈值距离的点。
【4】异端分子:
具有小局部密度而且距离高密度点很远的点。
分析图:
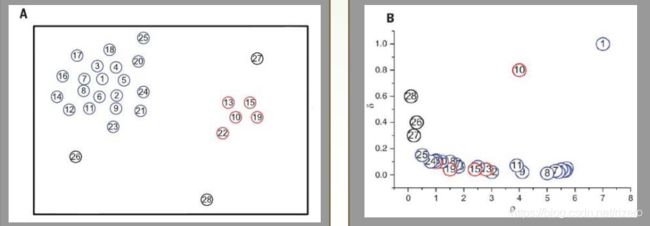
先看右图,我们可以看到,10和1点很明显独立出来了,因此,他们是聚类中心。
再看左图,我们可以看到27和28距离高密度点还是挺远的,因此我们把他们看成异端分子。
如果要密度聚类算法原理的话,你可以这样写:
过滤掉低密度区域的样本点,发现高密度区域的样本点
紧密相连的样本点被低密度区域分割,而且这些低密度区域的点距离其它高密度区域都比较远
算法过程:
- 计算空间中每个点的局部密度和高密度点距离,接下来将各点的( , )取值在平面坐标中标识出来。横坐标表示局部密度,纵坐标表示高密度点距离
- 找出聚类中心和异端分子
- 注意:不需要进行目标迭代优化
第九章 SOM神经网络聚类方法
SOM的全称是:Self Organizing Feature Map,翻译过来就是:特征自组织映射图
是我们利用神经网络进行聚类思路的一种
核心思想:一个神经网络接受外界输入信息的时候,会根据这些输入信息生成不同的特征映射域。这些特征域就代表了不同的类的形成。
SOM网络在保持点之间的邻近关系的前提下降维。
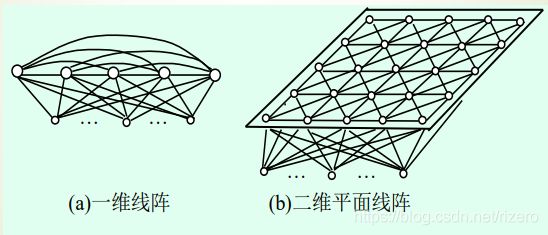
9.1 SOM网络的拓扑结构
- 输入层:接受外界信息
- 竞争层:对输入进行分析比较,生成特征映射。
9.2 SOM网络的学习算法
实际上,我们不难看到:从输入层到竞争层就是一个降维的过程
我们关键来看一下,到底是怎样生成特征映射的。
我们采取的是竞争学习的原理
当我们的网络获得一个新的输入向量的时候,我们就会把竞争层的对应的权重和这个输入向量进行相似性比较(这个相似性你可以采用欧氏或者余弦也可以),找出最相似的那个权重,然后把这个权重加强调整(所谓调整,就是把这个权重点靠这个输入向量偏移一下,至于偏移多少,由学习率决定)。
我们来抽象想象一下哈,我们的每个样本点,我们都可以看成是一个向量,之前我们无法对他进行很好的聚类的原因是他的维度太多了。不方便操作。
因此,我们需要输入层对他进行降维,降维成二维平面。
然后,我们可以想象:相当于把一张布铺到这堆被我们降维过的数据点上面。这张布,就是权重网,每一个点,就是神经网络里面的权重,一开始我们设随机值就行。
然后根据我们设定的竞争规则(就是距离最近的权重点为胜者)就依照我们设定的学习率进行位置偏移更新。
最后不断迭代出来的效果就像上面的图一样了,我们的权重网会被拉扯到不同的位置。
如果考试问过程,就这样写:
- 用随机数初始化多个权重向量 w j w_j wj,建立初始优胜域
- 接受向量输入 x i x_i xi
- 计算 x i x_i xi和 w j w_j wj的点积,寻找优胜权重节点
- 更新优胜域,根据学习率进行更新
例子利用SOM网络设计一个聚类降维:
- 输入层结点数:5(源数据维度)
- 输出层结点数:2(目标数据维度)
- 权重竞争层:70个神经元。
- 权重初始化:随机小数
- 学习率: a ( t ) = a ( 0 ) ( 1 − t / T ) a(t) = a(0)(1-t/T) a(t)=a(0)(1−t/T),这里的 a ( 0 ) a(0) a(0)是初始学习率,t是当前学习次数,T是总学习次数
- 优胜领域定义: N j ( i ) N_j(i) Nj(i)
考点预测
第一章:
【考选择】
- 常见的五类知识
- 数据挖掘的功能
第二章:
【考选择+填空】
数据预处理的技术
数据清洗:
- 缺失值的处理
- 噪声数据的处理(具体怎么算的,要清楚):分箱(等频,等宽),平滑(均值,边界,中值),回归(这个大概理解就行),
数据集成: - 卡方检验(怎么算的)
- 皮尔逊相关系数R,(区间和相关的判断)
数据变换:(三种规范的公式和计算方式) - 最小最大
- 零均值规范
- 小数定标
第三章:
【计算题,填空题】
一定自己手算出频繁项集表和列出规则表计算置信度
第四章:
【简答题】
记住ID3的决策树生成伪代码
知道C4.5用的是信息增益比,ID3使用的是信息增益
处理过拟合问题?
第五章:
【计算题】
考贝叶斯分类的计算
考贝叶斯信念网络的概率计算
第六章,第七章
【选择,简答】
人工神经元的激活函数,BP的原理:梯度下降法,SVM的理论基础是什么(统计,结构风险),核函数,SVM的优点缺点
第8,9章:
【计算,简答必考】
Kmeans,K中心点的手算步骤
密度聚类算法的原理和步骤
第10章:
【选择,简答题】
让你设计一个SOM网络,或者写一下SOM聚类算法的步骤。
数据挖掘抱佛脚专用精简版