智能机器人-（三）轮式，足式机器人的基本概念

---

---

一、机器人的移动方式设计

仿生足式机器人：点/面接触大，动静态稳定，爬坡/跨越障碍做功大，控制复杂度高。
人工轮式机器人：点接触，硬地板平面移动，动静态稳定，做功小，控制复杂度低。

二、足式移动机器人

1.足的规模

足数目越少，运动模式越复杂。

2.足的稳定性

静态稳定至少需要三条腿
（动态稳定）行进间稳定至少需要四条腿

3.足的自由度

足式机器人向前迈动至少需要2个自由度
一个对应抬起，一个对应摆动（x，z）
但只有两个自由度，在多个方向上的自由滑动是不可行的，因此多数情况下每条腿需要三个自由度。

踝关节是四个自由度
通过控制脚底板姿态，更好与地板接触，改善行走能力
增加运动自由度随之会增加控制设计的复杂度

毛虫利用液压使各退伸展，每个腿只有一个自由度
人腿有7个以上自由度，15个以上肌肉群。

4.足行步态

支持状态：腿处于支持状态时，腿的末端与地面接触，支持机器人的部分重量，并且能够通过蹬腿使机器人的重心移动。

转移状态：处于转移状态时，腿悬空，不和地面接触，向前或向后摆动。

步态：机器人各条腿的支持状态与转移状态随着时间变化的顺序集合。

周期步态：对于匀速前进的机器人，步态呈周期性变化。

实时步态：机器人能够根据传感器获取地面状况和自身的姿态，进而产生实时的步态。

对于多足移动机器人，存在运动时腿的协调或步态控制问题。其步态数目依赖于腿的数目。
对单条腿而言，步态是抬起与放下事件的序列，对于一个具有K条腿的的移动机器人，步行机器可能事件的总数N为

5.动力学考虑

传输代价：机器人行走一段距离所消耗的能量
大部分能量损失在腿的运动，启停间，加速和减速交叉阶段频繁能量传递，无法全部回收。
通过弹簧能储能元件减少能量消耗。

6.平衡控制

静态平衡，机器人的质心始终位于地面上的脚构成的支撑区域上，或是当两只脚都在地面上时的组合支撑区域上。
动态平衡，在步态的某个阶段，机器人的质心可能在脚的支撑区域外，典型的算法有：
零力矩点（ZMP）
倒立摆
神经网络
PID控制

7.常见足式机器人实例

双足仿人机器人智能行走系统
人体在行走的过程中，其重心不断地周期性移动和改变，在任何时刻至少有一只脚与地面接触，而其中一段是两只脚同时着地。单支撑和双支撑交替进行，但只有单支撑和双支撑在行走周期中所占比例合理，才能保持身体平衡。

双足行走周期的三个阶段：
1.单脚支撑阶段，摆腿阶段
2.双脚支撑阶段
3.移动过渡阶段

8.静态步行与动态步行

当机器人做静态步行运动时，身体的各个部分运动速度很小，机器人的整体稳定性较易控制。

如果机器人采用的是一种高速运动的步行方式，则称之为动态步行。

9.ZMP行走模型

重力和惯性力构成机器人的广义力，广义力的延长线落在地面上的点，即为期望的ZMP，对该点的广义力矩为零。
如果作用在机器人脚底的实际地面反力中心与期望ZMP重合，并落在支撑面上，则对于机器人无翻转力矩，从而使机器人处于稳定行走状态。
如果不重合则可能存在翻转力矩。

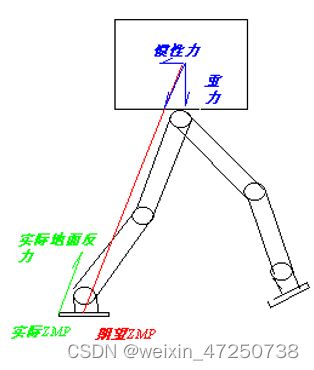
零力矩点（ZMP）和CoP（压力中心）是评价双足机构行走稳定性的重要参数。

支撑多边形
对于单腿支撑，支撑多边形就是支撑腿的足底接触面
对于双腿支撑，分为两种情况

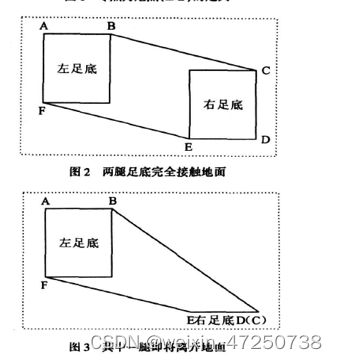
零力矩点始终落在支撑多边形内而不能落到边缘之外。
可以利用传感器检测ZMP的位置与支撑多边形边界进行比较判断行走是否趋于稳定。

当双足机构处于动态平衡时，ZMP和脚底所受地面反力的压力中心CoP时重合的。
在机器人脚掌放置FSR，用于测算实际行走中的ZMP。

计算整个机器人系统的实际ZMP按以下公式：

式子中X1、X2、Y1、Y2分别为左右脚ZMP点在参考坐标系中的坐标。Fz1、Fz2分别为左右脚4个压力传感器计算出的竖直方向的合力。

ZMP（零力矩点）控制是目前应用比较成功的双足机器人平衡理论，它要求ZMP点必须位于支撑面内。
根据任务要求设计双足机器人结构，得到重力的大小，再由运动轨迹规划确定重力的位置和惯性力，计算出期望ZMP位置，并进行稳定性分析和验证。保证期望ZMP落入支撑面内。
由于建模和计算误差，实际ZMP与期望ZMP会存在一定误差，可能会造成双足机器人的失稳，因此，必须实时监控期望ZMP与实际ZMP的偏差，并进行相应的补偿。

三、轮式机器人

轮式移动的效率高，轮式移动适用于大多应用场合，三轮足以保证移动平台的平衡。

1.轮子结构

标准轮：两个自由度（定向），绕轮轴和接触点旋转。
脚轮：三个自由度（万向），绕轮轴，接触点和脚轮轴旋转。
标准轮操纵独立完成，无副作用
脚轮操纵会引起附加力作用底盘
瑞典轮：三个自由度
球形轮

2.轮式移动平台的特征

（1）三个轮子可以保证平台的稳定性（静态）
重心要在三个轮子接触点组成的三角形内
更多的轮子可以增强稳定性（静动态）
需要柔性的悬挂系统
（2）大尺寸的轮子可以跨越更高的障碍

3.轮子的部署

差速驱动：转弯行驶或在不平路面上行驶时，使左右车轮以不同转速滚动，即保证两侧驱动车轮作纯滚动运动。

同步驱动：
所有的轮子转动被同一马达驱动- - -定义平台的移动速度
所有轮子的转向被同一马达驱动- - -设定平台的前进方向

四、移动机器人的空间坐标变换

未完待续…