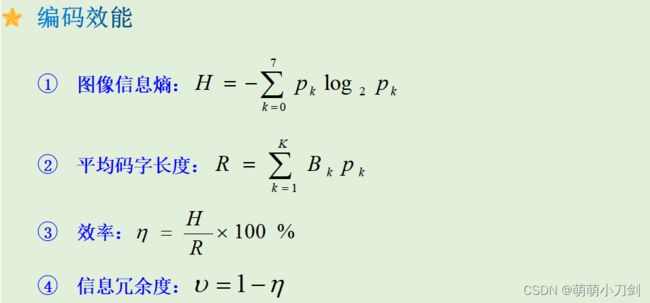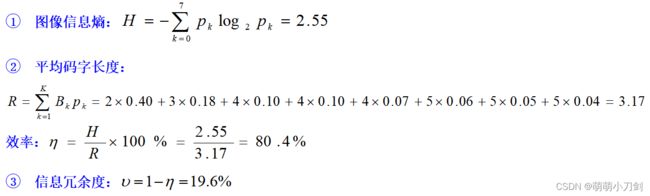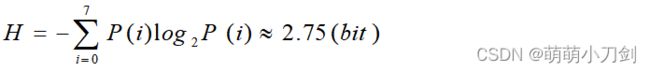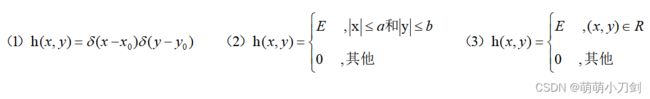《数字图像处理》题库5:计算题 ③
前言
这是我在学习数字图像处理这门课程时,从网络上以及相关书籍中搜集到的一些题目, 这些题目主要是针对期末考试的。 做题之前你需要注意以下几点:
- 这篇文章整理了第5种题型,即计算题的第3部分。
- 由于题目或答案中会出现许多的公式,重新编写很费时间,因此,我会将整个题目或答案截成图片来代替。
- 为了提高复习的效率,这篇文章从考试可能涉及到的各个考点出发, 将题目按照考点归类,每一个考点中包括知识点回顾、经典例题、举一反三这3个部分。
- 如果你需要举一反三中练习题的答案,可以前往我的个人主页下载对应的资源(整理不易,希望大家支持)。
考点21:香农—范诺编码
知识点回顾
香农—范诺(Shannon-Fannon)编码也是一种典型的可变字长编码。与哈夫曼编码相似,当信源符号出现的概率正好为2的负幂次方时,香农—范诺编码的编码效率可以达到100%。
香农—范诺编码的理论基础是符号的码字长度N i完全由该符号出现的概率来决定,对于二进制编码即有![]()
编码步骤
- 将信源符号按其出现的概率由大到小顺序排列,若两个符号的概率相等,则相等概率的字符顺序可以任 意排列;
- 计算出各概率符号所对应的码字长度N i;
- 将各符号的概率累加,计算累加概率P,即:

- 把各个累加概率P由十进制转换为二进制;
- 取二进制累加概率前N i位的数字,并省去小数点前的“0.”字符
- 即为对应信源符号的香农—范诺编码码字
经典例题
设一幅灰度级为8的图像中,各灰度级分别用S0、S1、S2、S3、S4、S5、S6、S7表示,对应的概率分别为0.40、0.18、0.10、0.10、0.07、0.06、0.05、0.04,对其进行香农—范诺编码。并分别计算图像信息熵,平均码字长,效率以及信息冗余度
将信源符号按其出现概率由大到小顺序排列,为0.40,0.18,0.10,0.10,0.07,0.06,0.05,0.04;
(2) 对于概率0.40对应的符号S0,根据(8-11)计算N0=2,将累加概率0.00转换位二进制小数为0.00,取前N0=2位,并去除小数点前的字符,即S0字符编码为00;
(3) 对于概率0.18对应的符号S1,根据(8-11)计算N1=3,将累加概率0.40转换位二进制小数为0.0110,取前N1=3位,并去除小数点前的字符,即S1字符编码为011;
(4) 对于概率0.10对应的符号S2,根据(8-11)计算N2=4,将累加概率0.58转换位二进制小数为0.10010,取前N2=4位,并去除小数点前的字符,即S2字符编码为1001;
(5) 对于概率0.10对应的符号S3,根据(8-111)计算N3=4,将累加概率0.68转换位二进制小数为0.10100,取前N3=4位,并去除小数点前的字符,即S3字符编码为1010;
(6) 对于概率0.07对应的符号S4,根据(8-11)计算N4=4,将累加概率0.78转换位二进制小数为0.11000,取前N4=4位,并去除小数点前的字符,即S4字符编码为1100;
(7) 对于概率0.06对应的符号S5,根据(8-11)计算N5=5,将累加概率0.85转换位二进制小数为0.1101100,取前N5=5位,并去除小数点前的字符,即S5字符编码为11011;
(8) 对于概率0.05对应的符号S6,根据(8-11)计算N6=5,将累加概率0.91转换位二进制小数为0.1110100,取前N6=5位,并去除小数点前的字符,即S6字符编码为11101;
(9) 对于概率0.04对应的符号S7,根据(8-11)计算N7=5,将累加概率0.68转换位二进制小数为0.11110100,取前N7=5位,并去除小数点前的字符,即S7字符编码为11110;
综上所述,S1-S7的香农—范诺编码如下:
| 灰度级 |
S0 |
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
| 编码 |
00 |
011 |
1001 |
1010 |
1100 |
11011 |
11101 |
11110 |
考点22:费诺—仙农编码
知识点回顾
费诺—仙农编码与Huffman编码相反,采用从上到下的方法。
香农-范诺编码算法步骤:
(1)按照符号出现的概率减少的顺序将待编码的符号排成序列。
(2)将符号分成两组,使这两组符号概率和相等或几乎相等。
(3)将第一组赋值为0,第二组赋值为1。
(4)对每一组,重复步骤2的操作。
经典例题
设一幅灰度级为8的图象中,各灰度所对应的概率如下表,要求对其进行费诺.仙侬编码。
| 灰度值 |
S0 |
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
| 出现频率 |
0.40 |
0.18 |
0.10 |
0.10 |
0.07 |
0.06 |
0.05 |
0.04 |
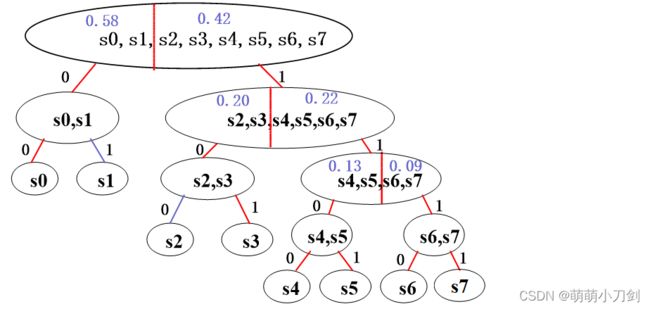
解:根据费诺—仙农编码的方法进行分组和赋值如下图所示
所得编码结果如下表
| 灰度值 |
S0 |
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
| 费诺—仙农码 |
00 |
01 |
100 |
101 |
1100 |
1101 |
1110 |
1111 |
考点23:LZW编码
知识点回顾
前几节中所覆盖的技术集中在消除编码冗余上。在这一节中,我们考虑一种致力于图像中的空间冗余的无误差压缩方法。称为Lempel-Ziv-Welch(LZW)编码的这种技术将定长码字分配给变长信源符号序列。
在第一定理的证明中,山农使用了信源符号编码序列这一思想,而不是单个信源符号。LZW 编码的关键特点是它不需要被编码符号出现的概率的先验知识。
LZW编码的原理
LZW 编码在概念上非常简单。
在编码过程的开始阶段,先构建一个包含被编码信源符号的码书或字典。对于8比特单色图像,字典中的前 256个字被分配给灰度值O.1.2,……,255。
当编码器顺序地分析图像像素时,不在字典中的灰度序列被放置在算法确定的位置(即下一个未用的位置)。
例如,如果图像的前两个像素为白色,则序列"255-255"可能被分配到 256 的位置,该位置后面的地址保留给灰度级 0 到 255。下次遇到两个连续的白色像素时,就用码字 256(即包含序列 255-255的位置的地址)来表示它们。
如果在编码过程中采用个9 比特、512字的字典,则最初用于表示这两个像素的(8+8)比特被单个9 比特码字替代。
很明显,字典的大小是一个很重要的系统参数。
- 如果字典太小,则匹配灰度级序列的检测将变得不太可能。
- 如果字典太大,则码字的大小反而会影响压缩性能。
LZW编码的特点
LZW 编码的一个独特的特点是,编码字典或码书是在对数据进行编码的同时创建的。很明显,在 LZW解码器对编码数据流进行解码的同时建立一个同样的解压缩字典。
多数实际应用都需要—种处理字典溢出的策略。一种简单的解决办法是,当字典已满时,刷新或重新初始化该字典,并使用一个新初始化后的字典继续编码。另一种复杂的选择是,监控压缩性能,并在性能变得低下或不可接受时刷新字典。此外,需要时,可跟踪并替换那些使用最少的字典词条。
经典例题
【冈萨雷斯《数字图像处理》第3版 P352 例题8.7】
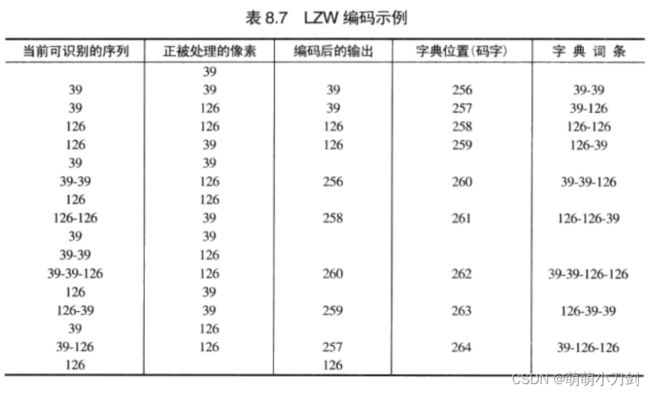
考虑下列大小为 4x4的8比特垂直边缘图像,并假设一个512字带有下列初始内容的字典(位置256到511开始时未使用)
下表中详细给出了对其16个像素进行编码的步骤。
图像按从左到右、从上到下处理其像素的方法来进行编码。每个连续的灰度值与表中称之为"当前可识别的序列"的第 1 列的一个变量链接。就像我们能看到的那样,该变量最初为空。
对每一个链接的序列搜索字典,如果找到了,如表中第一行的情况,则用新链接且可识别的序列(即位于字典中的序列)替代它。这可在第2行的第1列中实现。这既不产生输出代码,也不更改字典。
然而,如果没有找到链接的序列,则将当前可识别序列的地址作为下一个编码值输出,并将链接但不可识别的序列添加到字典中,当前可识别的序列则初始化为当前的像素值。这出现在表中的第 2 行。
最后两列详细给出了扫描整个4x4 图像时添加到了字典中的灰度序列。定义了9个附加的码字。编码结束时,字典包含 256个码字,且LZW算法成功地识别了几个重复的灰度序列,平衡它们将 128 比特的原图像降到了90 比特(即 10个9比特码)。从上到下读取第3列即可得到编码输出。得到的压缩率是1.42∶1(128:90)。
举一反三
【类似于 冈萨雷斯《数字图像处理》第3版 P400 例题8.19】
1、使用LZW编码算法,对7比特ASCII码字符串"aaaaaaaaaaa”进行编码
【冈萨雷斯《数字图像处理》第3版 P400 例题8.20】
2、为例8.7的LZW编码输出的解码操作设计一种算法。由于编码期间使用的字典此时不能使用,所以在对输出进行解码时必须重新生成码书。
考点24:压缩率
经典例题
对于扫描结果:aaaabbbccdeeeeefffffff,若对其进行霍夫曼编码之后的结果是:f=01 e=11 a=10 b=001 c=0001 d=0000。
- 若使用行程编码和霍夫曼编码的混合编码,压缩率是否能够比单纯使用霍夫曼编码有所提高?
- 若使用行程编码和霍夫曼编码的混合编码,压缩率是否能够比单纯使用行程编码有所提高?
原始扫描结果所占空间为:22*8=176(bits)
单纯霍夫曼编码的结果是:10101010001001001000100010000111111111101010101010101,共占53(bits)。压缩比为176:53.
单纯行程编码的结果是:4a3b2c1d5e7f,共占6(3+8)=66(bits).压缩比为176:66
Hufman与行程编码混合:41030012000110000511701 ,共占3+2+3+3+3+4+3+4+3+2+3+2=35(bits),压缩比为176:35. 即两个压缩比都有所提高。
举一反三
1、一图像大小为640×480 ,256 色。用软件工具SEA(version 1、3)将其分别转成24位色BMP,24位色 JPEG,GIF(只能转成256 色)压缩格式,24位色 TI FF压缩格式,24位色TGA压缩格式,得到的文件大小分别为:921,654 字节;17,707 字节;177,152 字节;923,044 字节;768,136 字节。分别计算每种压缩图像的压缩比。
2、某视频图像为每秒 30 帧,每帧大小为 512×512,32 位真彩色。现有 40 GB 的可用硬盘空间,可以存储多少秒的该视频图像?若采用隔行扫描且压缩比为 10 的压缩方法,又能存储多少秒的该视频图像?
考点25:区域分割、区域增长
知识点回顾
状态法(峰谷法、灰度阈值法)
基本思想:
- 确定一个合适的阈值T。
- 将大于等于阈值的像素作为物体或背景,生成一个二值图像。
- 阈值的选定可以通过如下图中灰度直方图确定。
方法:首先统计最简单图像的灰度直方图,若直方图呈双峰且有明显的谷,则将谷所对应的灰度值T作为阈值,按图右侧的等式进行二值化,就可将目标从图像中分割出来。
这种方法适用于目标和背景的灰度差较大、有明显谷的情况。
在四邻域中有背景的像素,既是边界像素。
简单区域扩张法
步骤:以图像的某个像素为生长点,比较相邻像素的特征,将特征相似的相邻像素合并为同一区域;以合并的像素为生长点,继续重复以上的操作,最终形成具有相似特征的像素是最大连通集合。这种方法称简单(单一型)区域扩张法。
具体步骤:
- 从图像最左上角开始,对图像进行光栅扫描,找到不属于任何的像素。
- 把这个像素灰度同其周围(4邻域或8邻域)不属于其他区域的像素的灰度值和已存在区域的像素灰度 平均值进行比较,若灰度差值小于阈值,则合并到同一区域,并对合并的像素赋予标记。
- 从新合并的像素开始,反复进行(2)的操作。
- 反复进行(2)、(3)的操作,直至不能再合并。
- 返回(1)操作,寻找新区域出发点的像素。
分裂合并法(基于四叉树思想的方法)
- 对于图像中灰度级不同的区域,均分为四个子区域。
- 如果相邻的子区域所有像素的灰度级相同,则将其合并。
反复进行上两步操作,直至不再有新的分裂与合并为止。
经典例题
1) 统计图象1各灰度级出现的频率结果为
p(0) = 5/64≈0.078 p(1)=12/64≈0.188 p(2)=16/64=0.25 p(3)=9/64≈0.141
p(4)=1/64≈0.016 P(5)=7/64≈0.109 p(6)=10/64≈0.156 p(7)=4/64≈0.063
2) 对于二值化图象,
若采用4-连接,则连接成分数为4,孔数为1,欧拉数为4-1=3;
若采用8-连接,则连接成分数为2,孔数为2,欧拉数为2-2=0;
2、对下图采用基于区域生长的方法进行图像分割,种子像素选为图中斜线画出的像素,给出生长准则为:邻近像素与当前区域灰度差值T<=2,选用8邻域,请画出这两种情况下的分割结果,重新作图,将分割出来的目标区域用斜线标明。
3、已知二值图像,如右图所示。 (1)对该图像使用四叉树进行划分; (2)用四叉树表达该图像。
举一反三
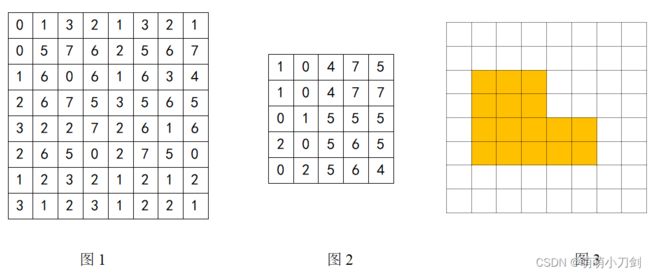
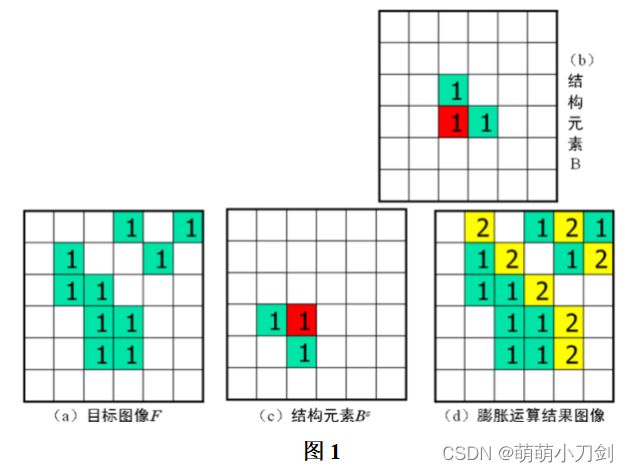
1、对下面的图像用状态法进行二值化,并计算二值图像的欧拉数(图1)
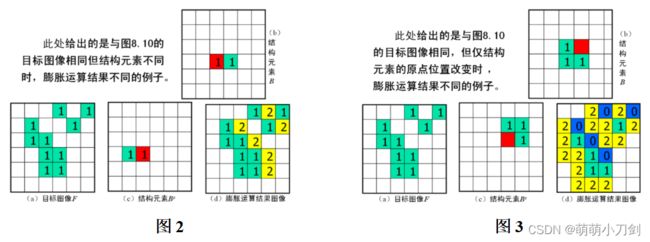
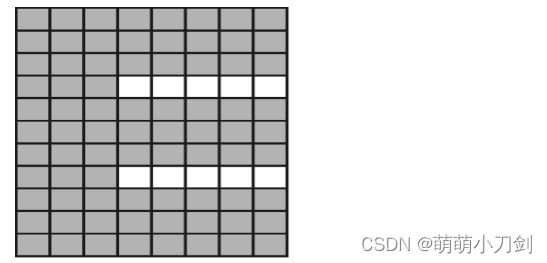
2、对下面的图像采用简单区域生长法进行区域生长,给出灰度差值 ①T = 1;②T = 3;③T = 8三种情况下的分割图像。(图2)
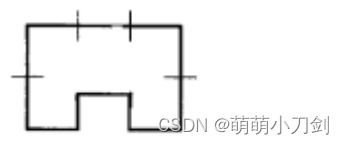
3、用分裂合并法分割图像,并给出对应分割结果的四叉树。(图3)
考点26:膨胀和腐蚀
知识点回顾
★ 膨胀
膨胀就是把二值图像各1像素连接成分的边界扩大一层的处理。
膨胀的原理:设二值图像为F,结构元素为B,Bs代表B关于原点对称的结构元素。当结构元素Bs的原点移到(x,y)处时,结构元素用![]() 表示。则图像F被结构元素B膨胀的定义式为:
表示。则图像F被结构元素B膨胀的定义式为:
含义:当结构元素Bs的原点移动到(x,y)位置时,如果![]() 所覆盖范围内的F的子图像与结构元素
所覆盖范围内的F的子图像与结构元素![]() 相应位置上至少有一个元素相同且不为0,则把该子图像中与
相应位置上至少有一个元素相同且不为0,则把该子图像中与![]() 的原点位置对应的(x,y)点的那个像素位置标注为1,否则为0。图像F上标注出的所有这样的像素组成的集合,即为膨胀运算的结果。
的原点位置对应的(x,y)点的那个像素位置标注为1,否则为0。图像F上标注出的所有这样的像素组成的集合,即为膨胀运算的结果。
膨胀运算的基本过程是:
- 求结构元素B关于其原点的反射集合Bs;
- 每当结构元素在目标图像F上平移后,结构元素Bs与其覆盖的子图像中至少有一个元素相交时,就将 目标图像中与结构元素Bs的原点对应的那个位置的像素值置为“1”,否则置为0。
注意:
结构元素中原点位置所对应的目标图像子图像位置处的值是0时,仍可进行膨胀运算,无需强求是1。当结构元素在目标图像上平移时,允许结构元素中的非原点像素超出目标图像范围。
结构元素形状对膨胀运算结果的影响:当目标图像不变,但所给的结构元素的形状改变时;或结构元素的形状不变,而其原点位置改变时,膨胀运算的结果会发生改变。
★ 腐蚀(或收缩)
腐蚀是把二值图像各1像素连接成分的边界点去掉从而缩小一层的处理。
腐蚀的原理:设F为目标图像,B为结构元素,则目标图像F被结构元素B腐蚀可定义为
含义:当结构元素B的原点移动到目标图像F中的(x,y)位置时,如果(x,y)处像素值为1,并且Bxy所覆盖范围内的F的子图像的其他像素能够包含Bxy的其他像素或与Bxy的其他像素完全相同,则保留该子图像中与Bxy的原点位置对应的(x,y)点的像素值1,否则均为0。图像F上保留的所有这样值为1的像素组成的集合,即为腐蚀运算的结果。
这里的“包含”是指结构元素B和目标图像F的子图像中值为1的像素两两之间的对应关系。
腐蚀运算的基本过程是:
把结构元素B看作为一个卷积模板,每当结构元素平移到其原点位置与目标图像F中那些像素值为“1”的位置重合时,就判断被结构元素覆盖的子图像的其它像素的值是否都与结构元素相应位置的像素值相同;只有当其都相同时,就将结果图像中的那个与原点位置对应的像素位置的值置为“1”,否则置为0。
注意:
结构元素中的原点位置处的像素值可以不为1,但要求目标图像中的子图像与结构元素B的原点对应的那个位置的像素值是1。
当结构元素在目标图像上平移时,结构元素中的任何元素不能超出目标图像的范围。
腐蚀运算的结果不仅与结构元素的形状(矩形、圆形、菱形等)选取有关,而且还与原点位置的选取有关。
★ 膨胀和腐蚀的作用
膨胀的作用是使孔洞收缩,目标扩大。对消除图像目标中的小颗粒噪声和填补凹陷非常有效。
腐蚀的作用是使目标收缩,孔洞扩大。对去除图像小颗粒噪声和目标之间的粘连非常有效。
★ 开运算V.S 闭运算
A、开运算(先腐蚀再膨胀):![]()
作用:光滑目标轮廓、消除小目标(毛刺和孤立点等),在纤细点处分离物体,同时并不明显改变目标面积;
B、闭运算(先膨胀再腐蚀):![]()
作用:在保持原目标的大小与形态的同时,填充凹陷、弥合孔洞和裂缝。
经典例题
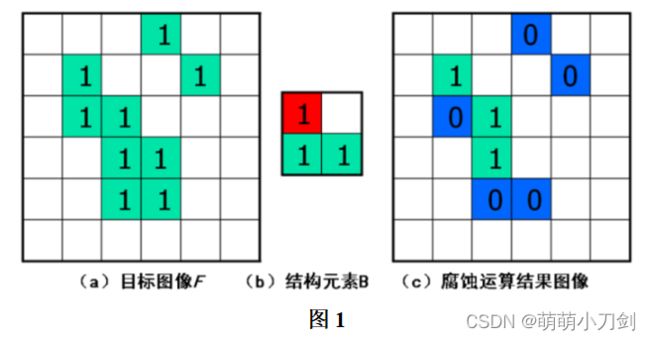
1、用结构元素B对目标图像F进行腐蚀运算。结构元素B中红色为原点。(图1)
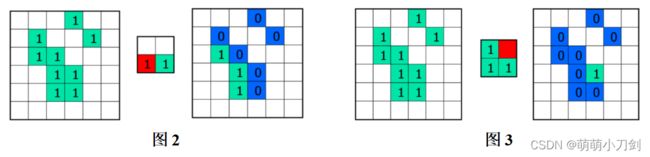
2、结构元素不同时的腐蚀运算(图2)、结构元素原点不同时的腐蚀运算(图3)
3、用结构元素B对目标图像F进行膨胀运算。结构元素B中红色为原点(图1)。
4、结构元素不同时的膨胀运算(图2)、结构元素原点不同时的膨胀运算(图3)
举一反三
1、请对下列左侧二值图片做开操作,其中深色代表1,浅色代表0,右侧为采用的结构元素。
2、请对下列左侧二值图片分别做开操作、闭操作,右侧为采用的结构元素。
3、请对下列左侧图片分别做腐蚀操作、膨胀操作,右侧为采用的结构元素。
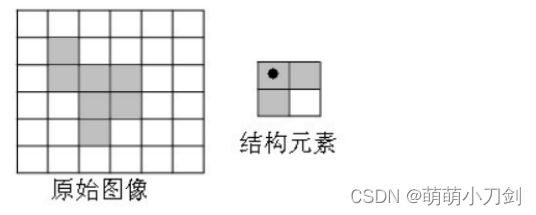
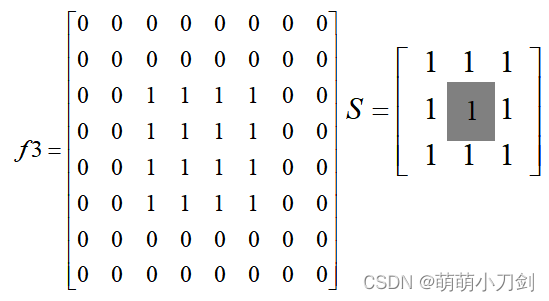
4、已知二值图象f3,写出用结构元素S(阴影处为原点)对其分别进行腐蚀和膨胀运算结果。
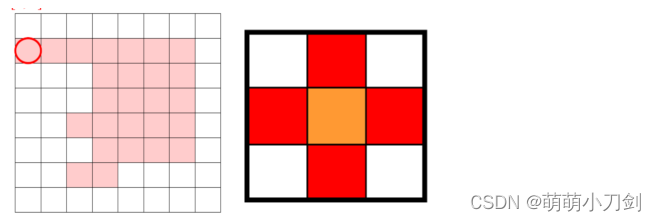
5、请采用适当的方法使下列图片中只保留竖直方向的米粒
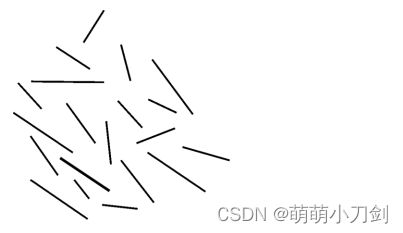
6、请采用适当的方法去除下列左侧图片中的一些线段,使最后图片的效果如右图所示
考点27:提取边缘
经典例题
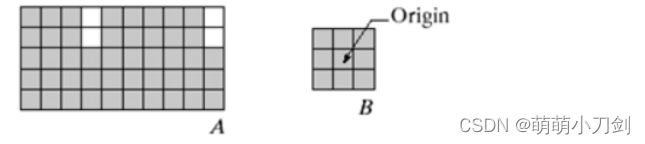
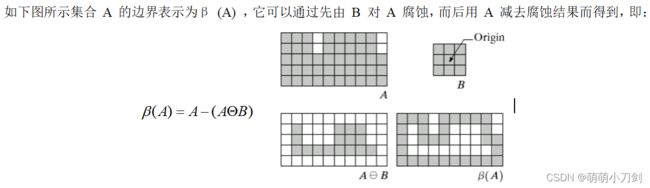
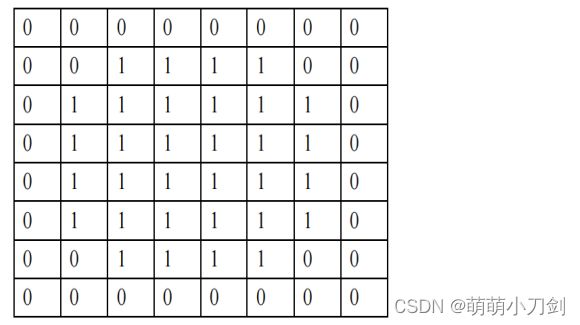
写出一个使用形态学算法提取边缘的方法,并用该方法提取下图 A 的边缘,给出步骤并画出结果图
举一反三
请采用适当方法提取下列图片中物体的轮廓边缘。
其他一些题目
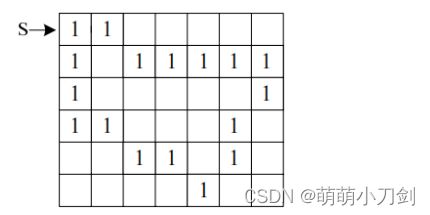
1、下图给出了一幅二值图像,用八方向链码对图像中的边界进行链码表述(起点是 S 点),
(1)写出它的八链码(沿顺时钟),并对该链码进行起点归一化,
(2)说明起点归一化链码与起点无关的原因。
(3)写出其一阶差分码,并说明其与边界的旋转无关;
(4)写出其形状数,并说明阶数。
2、求出链码0101030303323232212111的一阶差分
4、已知一个2X2的图片框的各方向投影如图所示,试求图片框内各像素的灰度值。
5、若灰度相似准则 V={1},试按四连通和八连通分别标出题图所示图像的目标物区域边界。
6、设工业检测中工件的图像受到零均值、与图像不相关噪声的影响。假设图像采集装置每秒可采集 30 幅图,若采用图像平均法将噪声的均方差减小到原来的 1/10,则工件需固定在采集装置前多长时间?
7、求下列数字图像块的二维 DHT(离散哈特莱变换)、二维 DWT(离散小波变换)
8、考虑在 x 方向均匀加速导致的图像模糊问题。如果图像在 t = 0 静止,并用均匀加速x0(t) = 1/2 at^2加速,对于时间 T, 找出模糊函数 H(u,v),可以假设快门开关时间忽略不计。
9、一个大小为 24mm×36mm 的 135 底片。在 36mm 方向上每隔Dmm 交替出现黑条和白条。你有一个 640×480 像素的数字化器。
- 对整个底片数字化能达到的最小像素间距是多少?
- 如果条纹为正弦型且 D=0.15mm,你能否对其数字化且没有混叠问题?
- 如 D=0.3mm,你能否使用2 倍过多采样?倍过多采样?
- 如 D=1mm,并且条纹是非正弦型的,能否计算其频谱到八次谐波(即 Sm=8×条纹的频率)?
10、某信号的功率谱为 Ps ( s ) = 10/∣s∣,噪声是白的并且不相关,其谱幅度为 2。画出维纳滤波器传递函数 H(s),及信噪功率比 R(s),(∣s∣< 20)。这是一个低通,带通,还是高通滤波器?
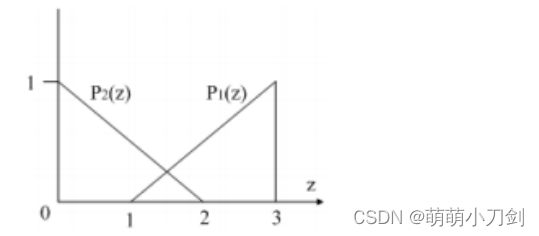
11、假设图像的灰度级概率密度如题图 7.2 所示。其中 p1( z)对应于目标,p2 (z )对应于背景。如果P1=P2,试求分割目标与背景的最佳门限。
12、某一线性移不变系统,其点扩展函数 h(x,y)是输入为![]() 时系统的输出,求下述情况下的调制转移函数 H(u,v)。
时系统的输出,求下述情况下的调制转移函数 H(u,v)。