Apollo课程学习5——规划

学习前言

今天的学习内容是规划。

什么是运动规划

一、运动规划概述

规划问题本质上是一个搜索问题，即对一个给定的函数，寻找最优解。相对于无人车而言，规划问题就是给定现在的状态，找到无人车移动的最优解，通常最优解目标函数F(x)定义。

从内容考虑，规划问题涉及三个领域，机器人领域，控制领域和人工智能。

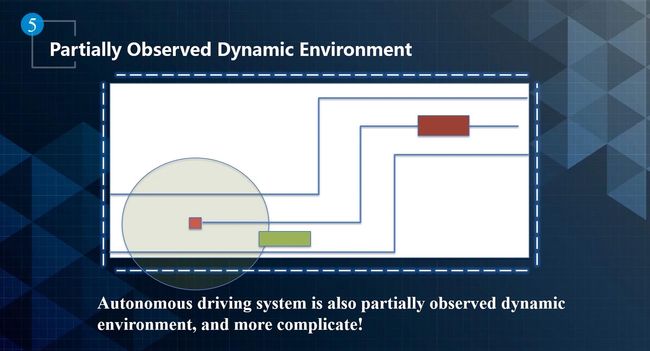
车辆状态、交通灯信息、障碍以及障碍轨迹、导航、高精地图都是规划模块能获得的信息。规划就是在这样的部分可见信息中给无人车找到一条轨迹，它不仅是一条路径，还包含路径信息和速度配置文件，需要保证速度和路径变化都是平滑的。

二、基本的运动规划

1、地图路线规划——高等级

路线规划的目标是找到从地图上的A前往B的最佳路径，路线规划使用了三个输入：地图、当前在地图上的位置、目的地。

在Apollo开始使用搜索算法查找路线之前，先将地图数据重新格式化为“图形”的数据结构，该图形由 “节点”（路段）和“边缘”（路段之间的连接） 组成。因为在计算机科学领域，人们已发现许多用于在图形中查找路径的快速算法，可以轻松地将图形上的路径重新转换为地图上的路径。

2、轨迹生成——低等级

处理不属于地图上的物体（如其他车辆、行人和自行车等），这些场景需要更低等级、更高精度的规划。轨迹规划的目标是生成免碰撞和舒适的可执行轨迹，该轨迹由一系列点定义。我们为每个路径点分配了一个时间戳和速度。

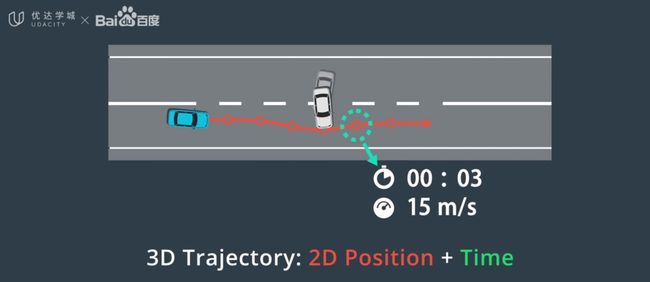
• 时间戳。将时间戳与预测模块的输出相结合，以确保我们计划通过时，轨迹上的每个路径点均未被占用。这些时间戳创建了一个3D轨迹。
• 速度。确保车辆按时到达每个路径点。

从最简单问题出发，把运动规划抽象成一个路径查找问题，只关心无人车怎样走，周围环境是不变的。如下图所示，我们将其抽象成无数的网格，从绿色的点到红色的点的路径规划就是一个path finding problem 。

三、A-star算法

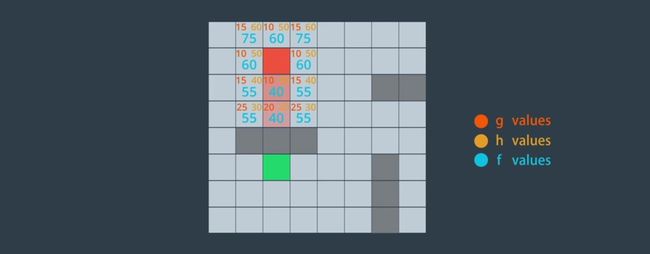
如下如所示，我们将网格中的每个单元格视为一个节点，网格中也包含一些阻挡潜在路径的墙壁（灰色部分）。从初始节点开始，我们需要确定8个相邻节点中最有希望的候选节点。根据具体情况可自定义成本估算方式。

• g值：从开始节点前往候选节点的成本。
• h值：从候选节点前往目的地的估计成本（启发式成本）。
• f 值：g值和h值的计算和，最佳候选节点是f 值最小的节点。

每当抵达新节点时，将重复此过程来选择下一个候选节点（尚未访问过且具有最小f值的节点）。

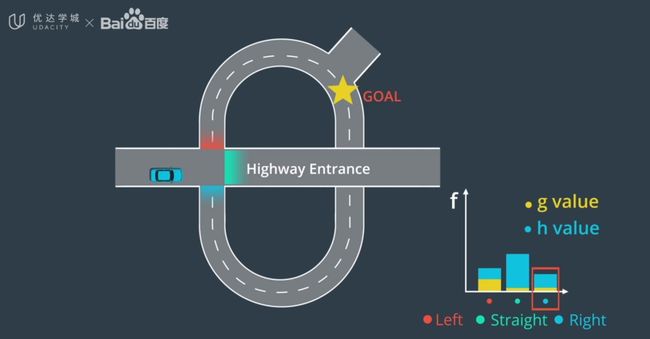
可以通过启发式方式对搜索问题进行优化。A-star算法是大概知道红点在右边，定义一个启发式函数，该函数猜测距离目标还有多远，通过这种方法先搜索一些比较近的点，然后从这个点出发逐渐扩大搜索圈，如下图所示。

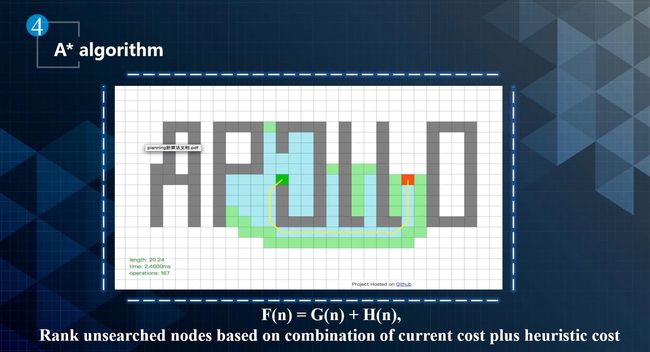
A-star花费时间比广度优先算法时间更短，因为它有信息支持，现在的一些路径搜索算法本质上都是从A-star算法出发，需要知道目标函数的样子。目前，A-star算法还不能直接用在规划模块上，因为A-star算法本身要求对整个环境全知。而自动驾驶对周围环境是部分观察的，如下图所示。

四、D-star算法

对于部分观察我们可以使用贪心算法，其实就是一个增量搜索，就是在看见的情况下尽量走好。

如下图所示，D-star算法利用当前能够看到的信息进行增量规划，D-star的特点是处理在看到的有限范围的条件下，如何到达预定地点的搜索问题方法，这种增量搜索很难通过一步步的迭代达到全局最优解。

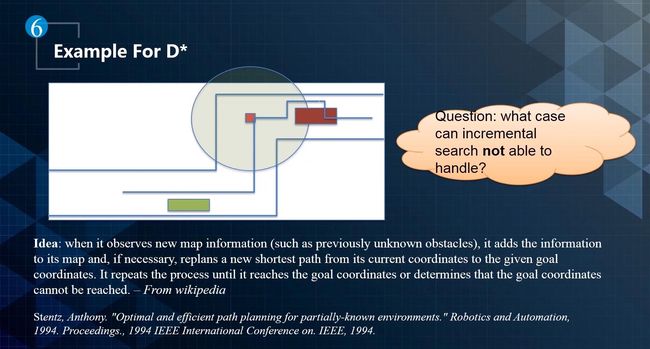
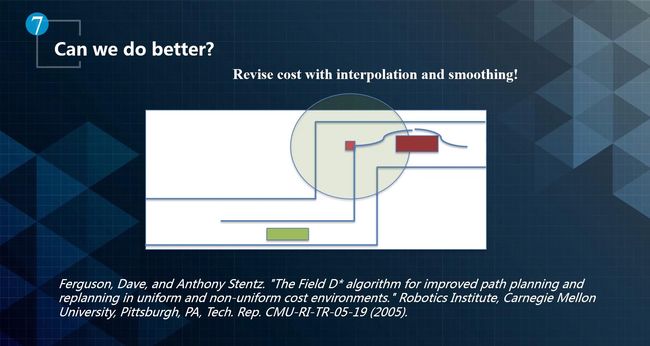
在现实生活中，人类开车是很少做90度直角转弯的，这样的折线并没有考虑无人车运动过程中的运动模型和动力学模型。可以通过平滑性曲线的方式来优化折线，如下图所示。

五、总结

1、ST图最终状态

• 巡航。车辆将在完成规划步骤后定速行驶，在时间 t 点以s点的速度巡航，最终状态的加速度为0。
• 跟随。在时间 t 时出现在某辆车后面，在跟随车辆时，需要与前方的车保持安全距离，速度和加速度将取决于我们要跟随的车辆。
• 停止。加速度和速度会被修正为0。

2、SL图最终状态

为了确保稳定性，汽车驶向的终止状态应该与车道中心一致，ST图轨迹应该车辆与车道线对齐并直线行驶而结束，如下图所示。为了达到这种终止状态，车的朝向和位置的一阶和二阶导数都应该为0，这意味着车辆既不是横向移动的，也不是横向加速的。

优化问题

一、目标函数的构建

1、运动规划的方法

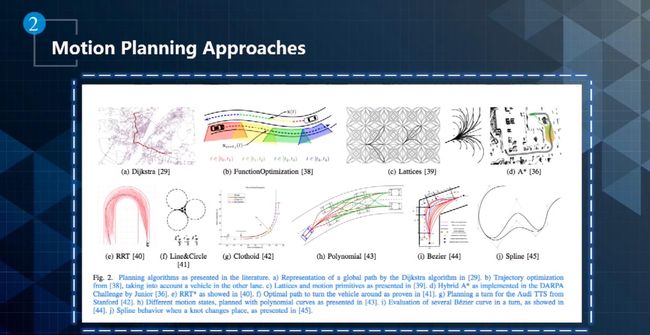
运动规划是在连续空间的一种优化，对于连续空间过程的优化往往比较难。因此，通常先将连续空间问题离散化表示，然后寻找对应的解决方案。如下图所示，可以使用图搜索的方法对离散空间问题进行求解。

规划问题中涉及到一些约束条件：

• Configuration Space （构造空间）
• 质点模型将运动轨迹当成一个点，在数学定义上是点和点没有交集，是不相撞的。但是不能把无人车看成一个点，因为在实际生活中一个车和一个车可是会相撞。
• 对于刚体而言，不仅是XY坐标，还要有heading信息才能研究跟障碍物之间的关系。对于无人车来说有更多的变量。其复杂性主要体现在两个方面（如图所示）：

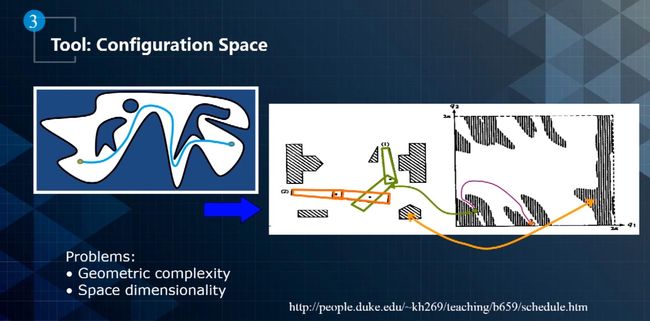
例如bounding box跟bounding box之间怎么相交，一个多面体跟一个多面体之间怎么检测出路径，以避免跟另一个障碍物相交。

• Roadmap
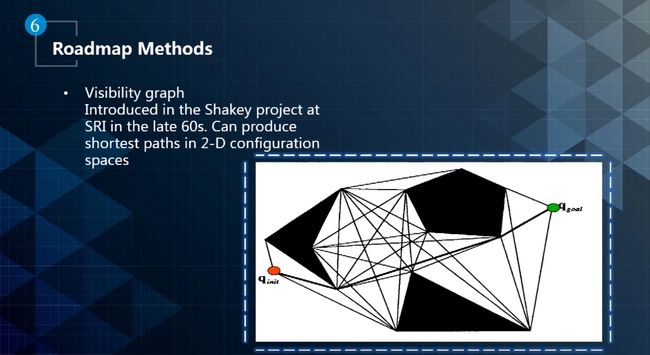
• 这个方法使用简单的连通图表示配置空间，类似于城市如何用地铁图表示。其中Visibility Graph是一种常用的Roadmap方法，如下图所示。Visibility Graph将起始节点，所有障碍物的顶点和目标节点相互连接来构建路线图。我们会发现，从红点到绿点的最短路径一定会通过靠近障碍物边界的折线。

• Cell decomposition（网格分解方法）：将整个空间分割成一个个cell，通过cell的连接图表示自由空间的连接属性。
• Potential field（势场法）：直接用微分方法处理。

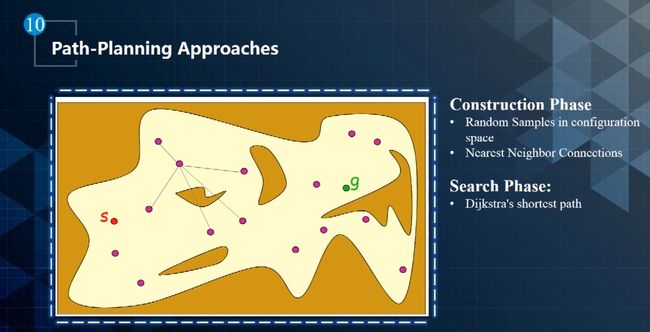
• PRM：
• 在整个配置空间随机采样一些点，如果点在障碍物上则去掉，然后将这些点连接起来，如下图所示的紫色点。从点s到g的最短路径就可以利用A-Star算法进行求解。但是该方法要求是对全局感知，而无人车是一个部分感知的应用场景，因此有RRT的改进方法。

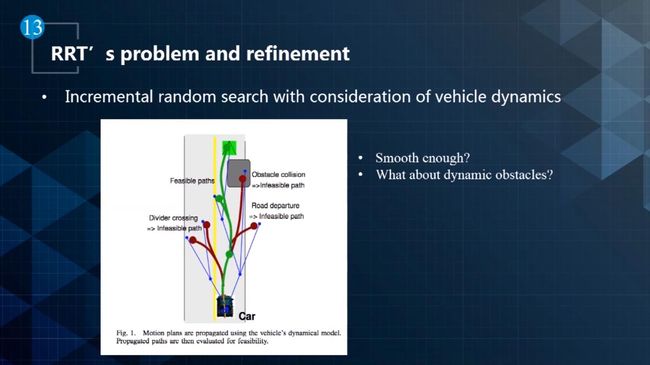
• RRT（基于快速扩展随机树算法）：
• 如下图所示，它构造一个根结点为起始点的配置空间树，通过随机采样增加叶子节点的方式，生成一个随机扩展树，当随机树中的叶子节点包含了目标点或进入了目标区域，便可以在随机树中找到一条由从初始点到目标点的路径。如果叶子节点和目标节点之间的连接被障碍物阻挡，则需要重新采样。

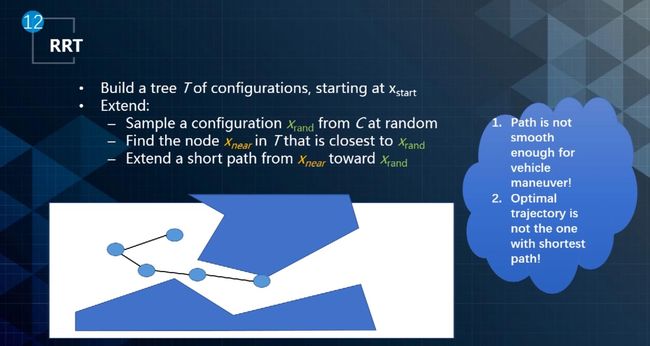
通过这种方式离散化的线是不适合无人车行驶的，因为这些线的curvature不连续，甚至curvature都没有。针对这一问题MIT提出使用平滑曲线进行连接的方法，如下图所示。但是该方法得到的路径可能还是不够平滑，另外对动态障碍物的处理也存在问题。

• Lattice网格方法
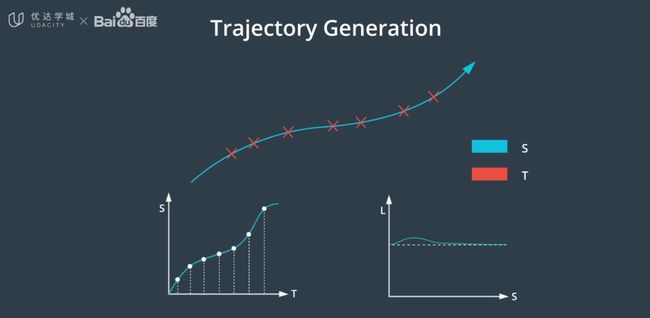
  通过使用Frenet坐标，我们可以将环境投射到纵轴和横轴上，将三维问题分解成两个单独的二维问题。
• ST轨迹：具有时间戳的纵向轨迹。
• SL轨迹：相对于纵向轨迹的横向偏移。

Lattice规划首先分别建立ST和SL轨迹，然后通过s值进行匹配来合并轨迹，构建由二维路径点和一维时间戳组成的三维轨迹，最后对预选模式中的多个候选最终状态进行采样，使用成本函数对这些轨迹进行评估，并选择成本最低的轨迹。

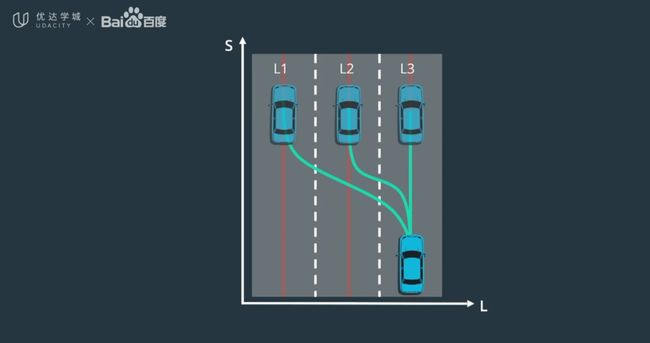
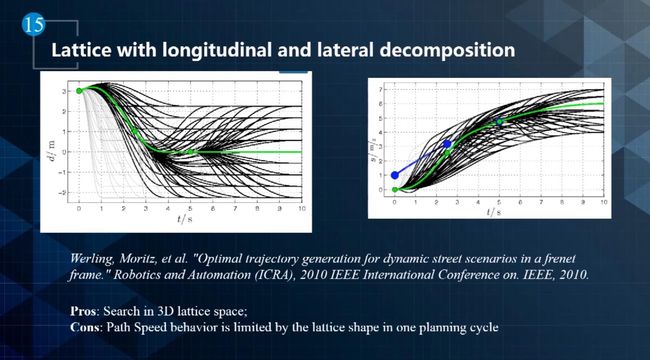
• 如下图所示，最原始的 Lattice网格方法非常简单，它在XY世界坐标系中，以1米为单位进行网格划分，然后用无人车可以行进的、曲率连续的曲线将起始点和目标点连接起来。
• 但是对于道路来说，这种抽象方式并不合适。Lattice Sampling撒点不能在规则化坐标系下去撒点，因为道路并不是一个完全XY的坐标系。因此提出了在sl坐标系下进行离散的方法Lattice in Frenet Frame。

当抽象出这些点之后，要使用平化曲线连接。

• Splines方法：使用螺旋曲线的方法。

• Polynomial方法：使用路径-速度迭代优化的方法对Lattice方法进行优化，它将问题降维，分成了path 和 speed两个维度逐渐优化，这是一种iterative的处理方式。

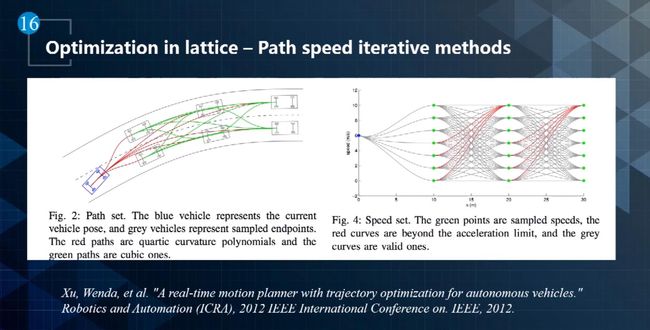
还可以用Functional Optimization方法对运动规划进行处理，对整个问题建模，设计相应的代价函数。二次规划就是其中一种常用的方法。

2、总结

二、约束条件（环境变化）

1、运动规划概述

运动规划根据环境的变化在算法和处理方法上有很大的不同，涉及到模型建立、平滑优化和坐标转换以及障碍物投影等。如下图所示。

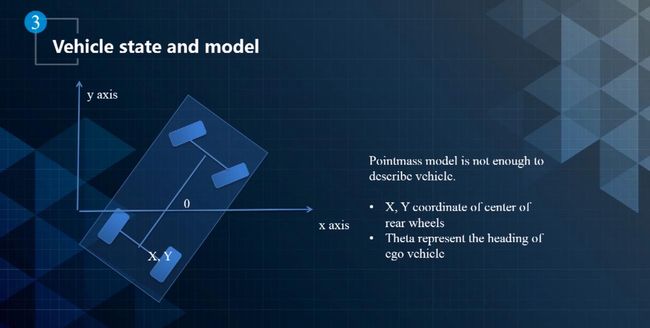
2、车辆模型的建立

对于汽车而言，质点模型是远远不够的，无人车是前轮转向的车，前后位置的变化是不一样的。

• 自行车模型：
• 可以将汽车的四轮抽象成两个轮子，前轮中心和后轮中心的运动方向和自行车一样。车辆在垂直方向的运动被忽略掉，用一个二维平面上的运动物体来描述车辆的运动模型。
• 自行车运动的时候具有以下特点，旋转车头的时候，前轮和后轮都围绕一个中心点转动，并且后轮的转向半径（1/k）(1/k)与方向盘转动角度w满足下图所示关系，其中L为前轮中心和后轮中心的距离。

在实际的自行车运动模型中，后轴中心是沿着如下图所示的一条平滑的轨迹运行，该轨迹对应的曲率(k)表示调整方向盘的度数，如果为正，表示向左转，反之则向右转。

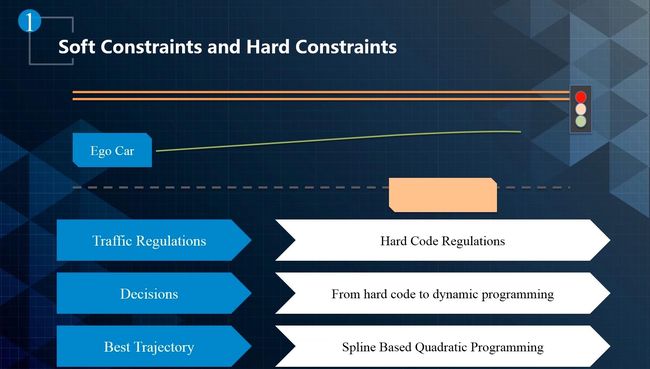
• 在实际过程中无人车的去抽象约束：
• 在这个场景中，有三类约束，这些限制又分为硬限制和软限制，例如交通规则属于硬性限制。

3、曲线坐标系转换

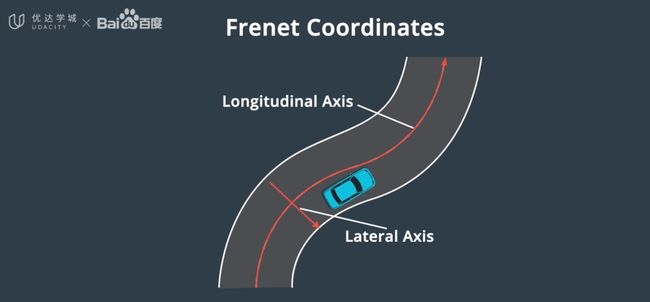
• Frenet坐标
  我们常用的笛卡尔坐标系对车辆来说并不是最佳选择，所以选用可描述汽车相对于道路的位置的Frenet坐标。
• 纵坐标s：代表沿道路的距离。
• 横坐标d：表示汽车偏离中心线的距离。

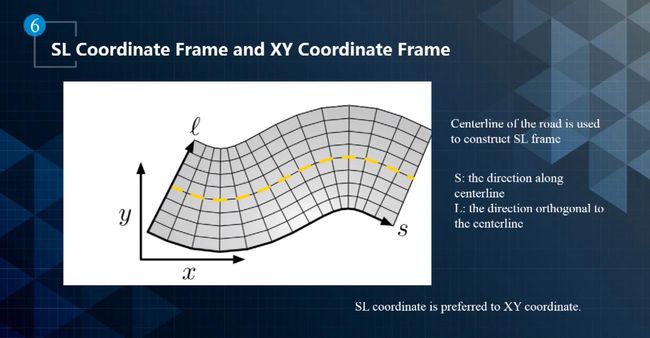
• SL坐标系也称为frenet frame。
• 它以道路中心线为参考，S表示道路中心线的方向，L表示与道路中心线垂直的方向。
• 在结构化道路上行驶的时候，SL坐标系比XY坐标系更加贴合实际需求。

• SL坐标系到XY坐标系的投影：
• 之所以要投影到世界坐标系，是因为很多信息是全局的，例如红绿灯位置，参考的是XY世界坐标系。
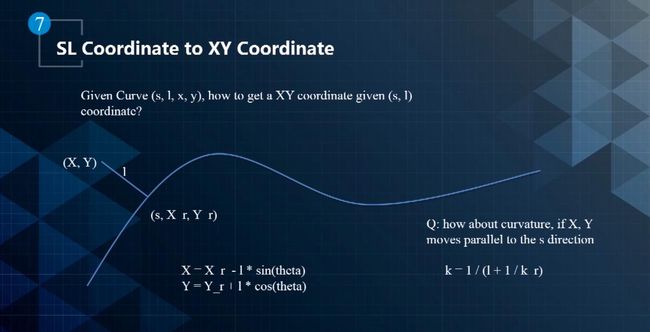
• 在给定SL坐标系时，每一个点的S坐标本身对应一个（x-r,y-r）坐标，根据该点的横向偏移距离，可以求出给定点在世界坐标系中的XY位置，如下图所示。其中theta是参考线的方向，也就是切线方向。

• XY坐标系到SL坐标系的投影
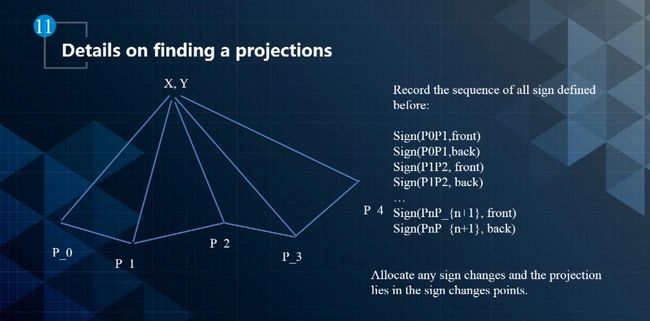
• 投影点是经过XY坐标，且垂直于曲线的线段与曲线的交点。因为SL坐标系并不是唯一的，XY会在曲线上产生很多投影，如下图所示XY就有两个投影点。通常情况下会增加一些限制，例如投影距离不能超曲率值。需要注意的是，掉头的时候还是需要特殊处理的。

4、轨迹平滑的方法

在自动驾驶中，我们将环境抽象成 SL 坐标系，在此坐标系下的曲线光滑度是有要求的。首先，曲线本身要平滑，其次曲率也要满足平滑的特性。因此需要对轨迹线进行平滑处理。

也不能先生成一条线，然后再进行平滑；不能对 Curvature 进行一个后期的平滑，因为 XY 坐标本身与 Curvature 是有联系的，不能单独平滑曲率，也不能单独平滑 X 或者 Y。

• 多项式：
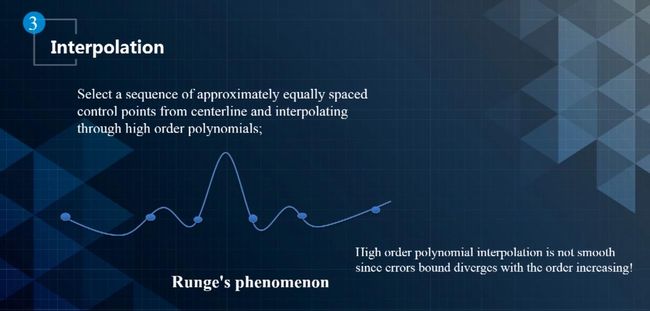
• 首先，可以在轨迹上以等距离的方式随机选择一些点，然后用高阶多项插值的方式来近似表示轨迹，对多项式进行优化。但是高阶多项式不能用于平滑，因为高阶的多项式抖动太大，没有办法控制幅度，这就是常说的龙格现象，如下图所示。

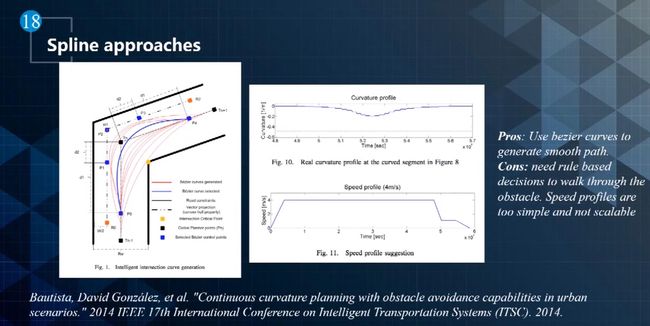
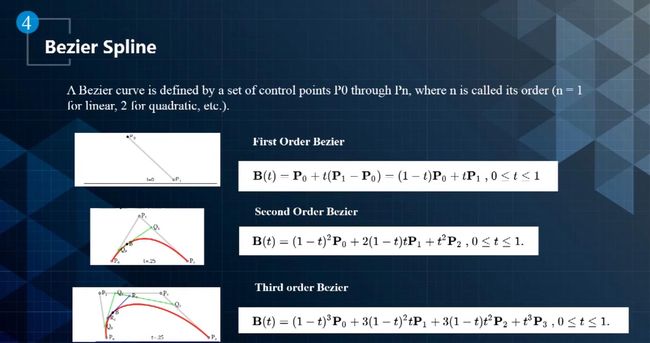
• Bezier Spline：
• Bezier Spline 曲线是由一系列控制点定义的，其中n代表曲线的阶数。如下图所示，分别给1阶、2阶、3阶Bezier Spline曲线的表示形式。通过对它们做平滑，得到平滑的曲线，例如二阶平滑保证曲线的曲率平滑。

• Bezier Spline方法的缺点：

• Smoothing Spline：
• 定义平滑最简单的方法就是最短路径，但是路径最短还不能保证平滑性，因此会对其不同阶导数进行 Minimize 求解，保证导数空间的连续，这就是Smoothing Spline最初的思想。
• 一维平滑度定义：

• Smoothing Spline 具有一些特殊的性质，在给定边界的条件下，它是一个多项式，可以找到最优解。但是它的 Boundary Constraint 只考虑了起点和终点，如果中间有障碍物就不是最优解。
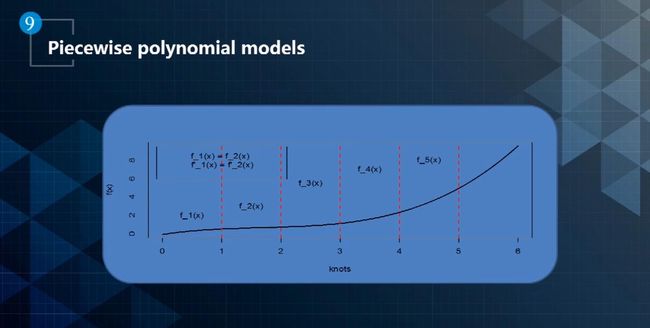
• 这种情况下可以使用 Piecewise Polynomial（分段多项式） 来处理：

• 一个 Piecewise Polynomial 是一维的函数，描述二维曲线是不够的。
• Spline 2D：
• 假设我们把曲线分成 N 截，每节曲线段它的 X 坐标是一个 Polynomial ，Y 坐标也是一个 Polynomial 。如下图所示，用 5 阶多项式来表示 X 和Y，称之为 Quintic Spline（五次样条），每一节都是这样的函数。这种表示有一个很好的特性，就是目标函数具有旋转不变性。
• 我们让它在 X 坐标上的变化率，也就是三阶导的平方是最小的，Y 上的变化率三阶导也是最小的，代价函数就是这两个变化率的和。代价函数的求解就是一个二次规划问题。

• 螺旋曲线：
• 通过一个极坐标形式定义，比如说沿着一条曲线，如果一个点 S 的曲率是知道的，可以唯一定义出一条经过 S 的曲线，也就是 Spiral Path 。那么可以让 Spiral Path 满足起点、终点约束条件生成一条螺旋曲线。

• 方法比较：
• 任何的曲线在足够密的时候都可以用Piecewise Spiral path 或者是 Piecewise Polynomial 表示。
• 但是它们的出发点不一样，Polynomial 计算很快很简单，Spline 2D 是一个凸空间里面生成一个 Spline 曲线。Spiral Path 是从 Configuration Space 出发。
• 理论上来讲，螺旋曲线生成的线是要比 Spline 更好处理，对一些极端情况处理更好。

5、轨迹的评估

• 轨迹应能免于碰撞，必须无障碍物。
• 要让乘客感到舒适，路径点之间的过渡以及速度的任何变化都必须平滑。
• 路径点对车辆实际可行，不能构建包含不可行机动的轨迹。
• 轨迹应合法，我们需要了解每个路径点的交通规律，并确保轨迹遵守这些法律法规。

车辆在不同的环境中使用不同的成本函数选择最佳轨迹。

三、求解方法

1、路径-速度解耦规划

1.1 动态规划

• 路径规划:
• 我们首先将路段分割成单元格，然后对这些单元格中的点进行随机采样，通过从每个单元格中取一个点并将点连接，通过重复此过程，我们就创建了多个候选路径。然后使用自定义的成本函数对每条路径进行评估，选择成本最低的路径。

• 速度规划:
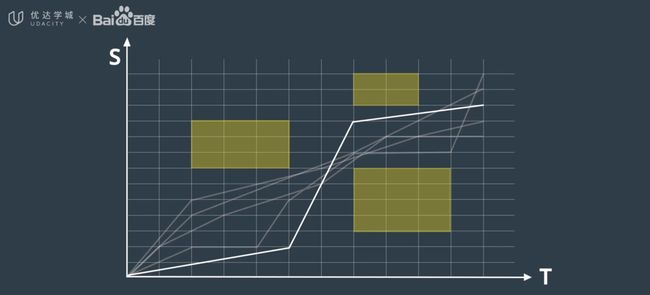
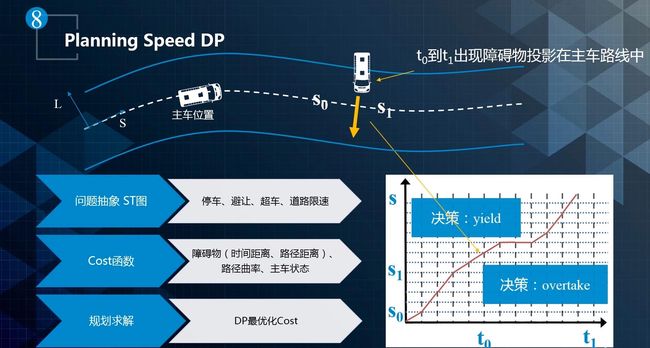
• 我们首先将ST图离散成多个单元格，单元格之间的速度有所变化，但每个单元格内速度保持不变。将障碍物绘制为在特定时间段内阻挡道路的某些部分的矩形（黄色部分），为避免碰撞，速度曲线不能与此矩形相交。接着，我们便可以使用优化引擎来搜索受到各种限制的低成本解决方案，选择最佳的速度曲线。

• 动态规划通过类似于有限元的方式，把问题从连续空间抽象成离散空间，然后在离散空间中进行优化。
• 虽然这种方法可以逼近连续空间中的最优解，但是计算复杂度很高，计算时间长。

1.2 二次规划问题

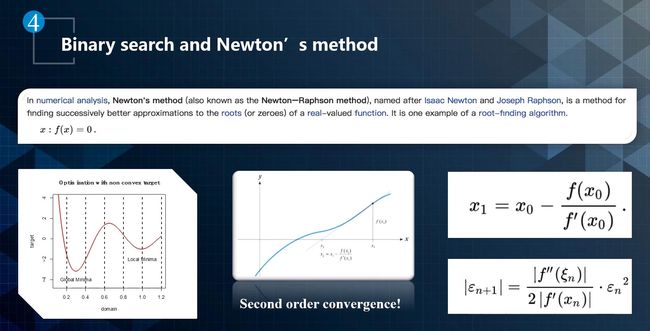
路径-速度解耦规划很大程度取决于离散化，尽管离散化使这些问题更容易解决，但生成的轨迹并不平滑，我们使用二次规划将平滑的非线性曲线与这些分段式线性段拟合，可将离散解决方案转换为平滑轨迹。最后我们将路径和速度曲线合并构建轨迹。

• 带约束的二次规划问题：

求解二次规划问题的方法 KKT：

2、总结

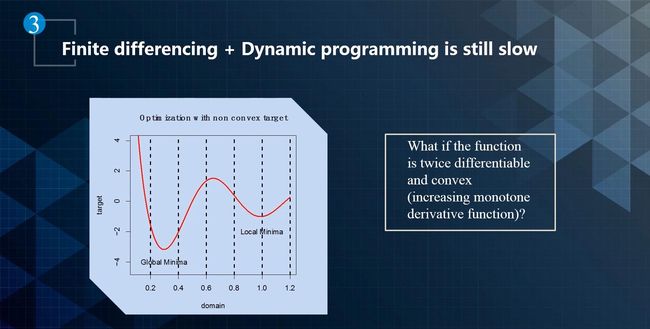
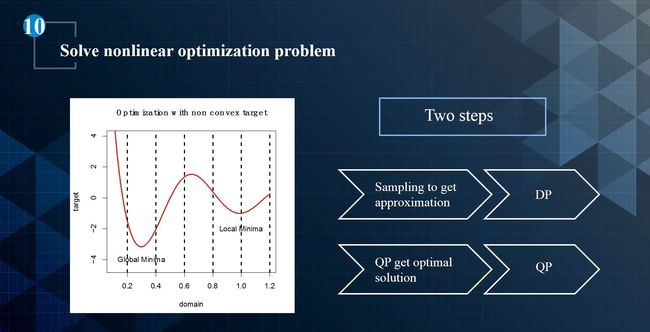
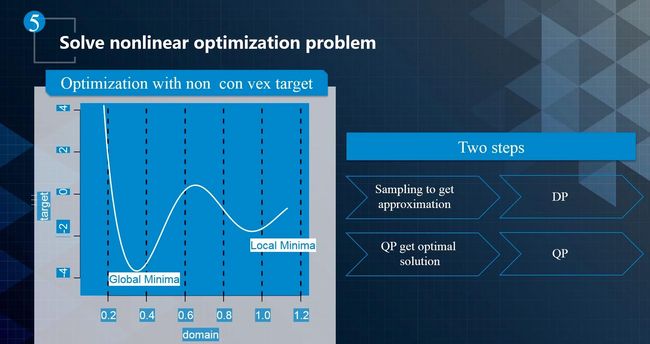
总的来说，对于求解非线性优化问题（自动驾驶中的规划基本都是非线性的），通常就是用启发式方法来求解。先用动态规划给出一个粗略解，给出一个凸空间。然后用二次规划方法在凸空间里去寻找最优解，如下图所示。

Apollo EM Planner

一、Apollo EM规划框架

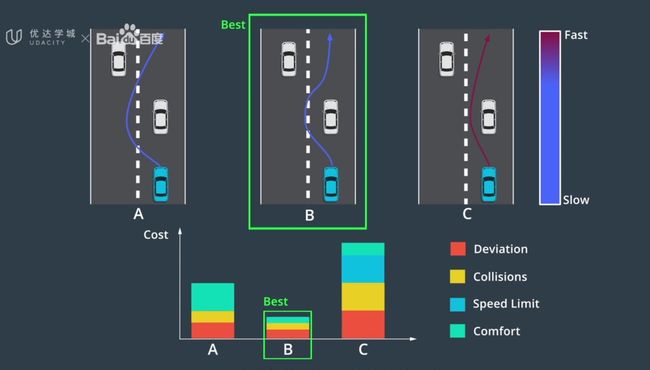
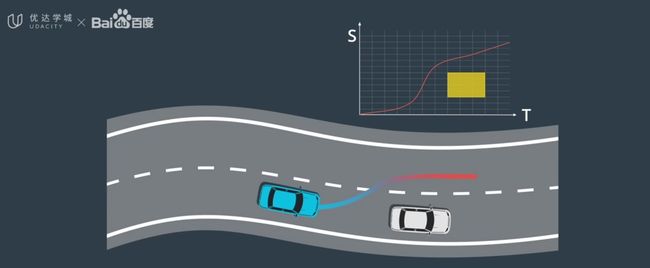
Apollo 设计了一个 EM 规划框架来处理不同的场景，如下图所示，展示处理一个换道场景。

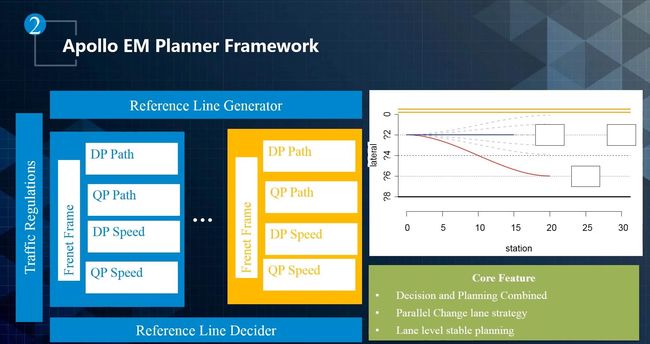
在蓝线和红线交点处发现前方有车辆行驶缓慢，可能要进行换道处理。在 Apollo EM 规划框架中，会对换道和继续在本车道行驶分别规划出一条轨迹，只有换道之后的 Trajectory 要比本车道的 Trajectory 好的情况下才换道。

在 Apollo 的 EM planner中，决定哪个道比较好的模块叫做 Reference Line Decider，中间的并行模块是通过 Path Speed Iterative 的方式并行实现的。

二、优化决策问题

优化决策问题本身是一个 3D optimization 问题，其中包含了三个维度，需要生成 SLT 。三维空间的优化相对比较复杂，常用的方法有两种：

• 一种就是离散化的方式去处理。
• 另一种方法是 Expectation Maximization（期望最大化）。其基本思想是降维处理，先在一个维度上进行优化，然后在优化的基础上再对其它维度进行优化，并持续迭代以获得局部最优解。

对于无人车，Apollo 上的 EM planner 对 Path-Speed 进行迭代优化，如下图所示：

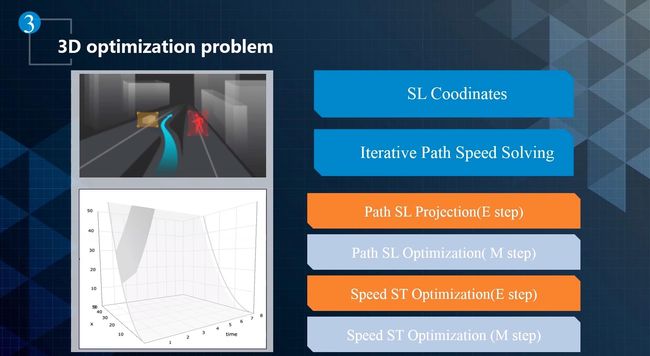
首先，生成一条 Optimal Path ，在最优路径的基础上生成 Optimal Speed Profile 。在下一个迭代周期，在优化后的 Speed 的基础上，进一步优化 Path，依次类推。它分了四步走，其中分为两步 E step 和 M step 。这种算法的缺点是不一定能收敛到全局最优解。

• 优化问题的关键步骤：

三、非线性优化问题

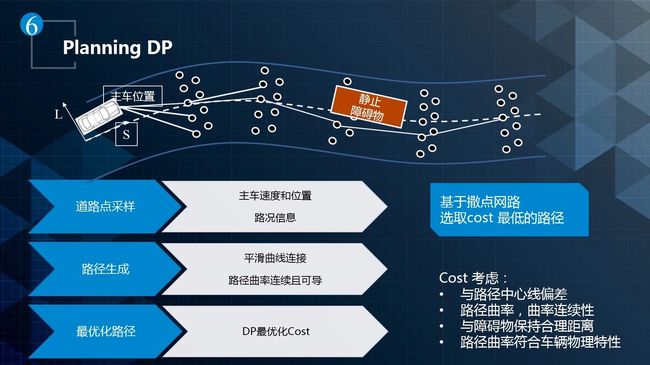
对于非线性优化问题，通常都是分两步走：一是动态规划，先找一个粗略解。然后再是二次规划，从粗略解出发，找出一个最优解。

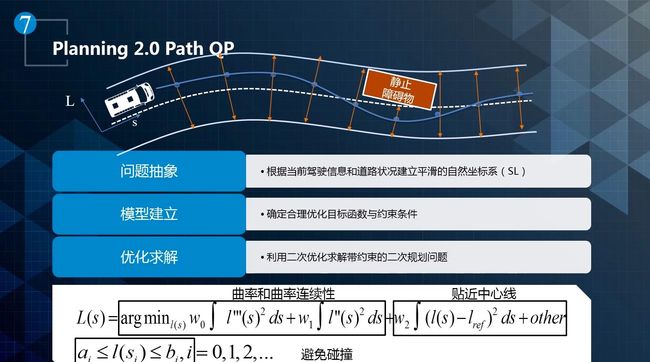
• 以路径规划为例，假设前方有一个障碍物，首先做出从左边还是右边的避让决策，然后通过 QP 生成一条平滑的曲线去避让障碍物。

• 对于速度而言，先通过动态规划的方式给出一个粗略的解，然后再通过二次规划的方式给出一个更平滑的解。