特征归一化总结（Feature Scaling）

写在前面

最近在研究基于小样本的故障诊断问题，看到很多关于利用数据驱动中深度学习的方法来优化故障诊断问题中，部分文献会通过“归一化”的方式，优化步骤，从而达到较少训练样本数或者节省训练时长。之前对归一化有过一定接触，但是不太了解。刚好趁此机会，将网上的一些归一化方法进行整理和总结。

纯粹自己学习整理，侵权删。

也参考了部分笔记：

https://www.cnblogs.com/shine-lee/p/11779514.html（给了我很多建议，其中很多也都在这里有一些摘抄）

https://www.zhihu.com/question/20455227/answer/197897298

特征归一化（Feature scaling）-WHY

Feature scaling，常见的提法有“特征归一化”、“标准化”，是数据预处理中的重要技术。他的重要性：

（1）特征间的单位（尺度）可能不同，比如身高和体重，比如摄氏度和华氏度，比如房屋面积和房间数，一个特征的变化范围可能是[1000,10000]，另一个特征的变化范围可能是[−0.1,0.2]，在进行距离有关的计算时，单位的不同会导致计算结果的不同，尺度大的特征会起决定性作用，而尺度小的特征其作用可能会被忽略，为了消除特征间单位和尺度差异的影响，以对每维特征同等看待，需要对特征进行归一化。

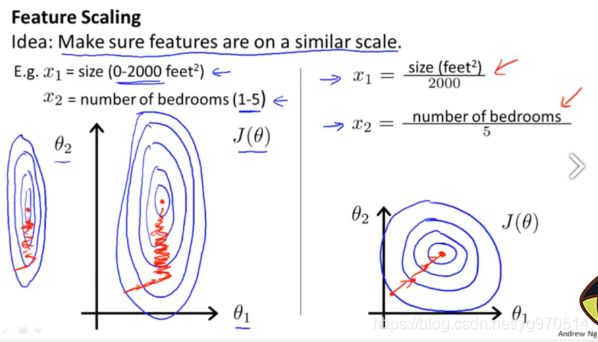
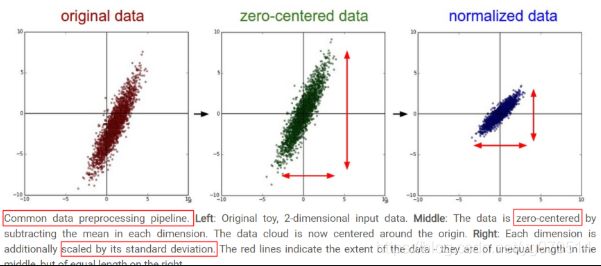
（2）原始特征下，因尺度差异，其损失函数的等高线图可能是椭圆形，梯度方向垂直于等高线，下降会走zigzag路线，而不是指向local minimum。通过对特征进行zero-mean and unit-variance变换后，其损失函数的等高线图更接近圆形，梯度下降的方向震荡更小，收敛更快。这个下图尤其形象，摘抄至Andrew Ng

数据归一化后，寻优解的寻优过程明显会变得平缓，更容易正确收敛到最优解。
#wiki指出
（1）归一化后，加快了梯度下降求最优解的速度
（2）归一化有可能提高精度。因为有些分类器需要计算样本间距离
为什么需要激活函数
如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层节点的输入都是上层输出的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。
激活函数实际就是让整个网络仿真出来的模型逼近任何函数，

关于归一化和标准化

一维数据的缩放有如下定义：

1、归一化：

2、标准化：

其实归一化和标准化的本质就是一种线性变换。

线性变换为什么不会使变换后的数据“失效”？

答：线性变化不改变原始数据的数值排序（线性变换保持线性组合与线性关系式不变）；

区别：

归一化的缩放是“拍扁”统一到区间（仅由极值决定），而标准化的缩放更是“弹性”和“动态”的，和整体样本的分布有很大的关系。

归一化：缩放仅仅跟最大、最小值的差别有关。——输出在0-1之间

标准化：缩放和每个点都有关系，通过方差（variance）体现出来。其中每个数据点都有贡献量。——输出范围是负无穷到正无穷

部分小tip：

如果对输出结果范围有要求，用归一化

如果数据较为稳定，不存在极端的最大最小值 ， 用归一化

如果数据存在异常值和较多噪声 ， 用标准化。可以间接通过中心化避免异常值和极端值影响。

特征归一化的方法（wiki）

Rescaling (min-max normalization、range scaling)：

$$x^{\prime }=a+\frac{(x-\min (x))(b-a)}{\max (x)-\min (x)}$$

将每一维度特征线性映射到目标范围[a, b]，常用为[0, 1]和[-1, 1]。假设到[0,1]
$$x^{\prime }=\frac{x-\min (x)}{\max (x)-\min (x)}$$

Mean normalization

$$x^{\prime }=\frac{x-\bar{x}}{\max (x)-\min (x)}$$

将均值映射为0

Standardization (Z-score Normalization)

$$x^{\prime }=\frac{x-\bar{x}}{\sigma }$$

每一维特征0均值1方差：（zero-mean and unit variance）

Scaling to unit length

$$x^{\prime }=\frac{x}{\Vert x\Vert }$$

对样本特征向量长度进行归一化。长度的度量常使用：欧氏距离

上述4种feature scaling方式，前3种为逐行操作，最后1种为逐列操作。

计算方式上对比分析

前3种feature scaling的计算方式为减一个统计量再除以一个统计量，最后1种为除以向量自身的长度。

减一个统计量可以看成选哪个值作为原点，是最小值还是均值，并将整个数据集平移到这个新的原点位置。如果特征间偏置不同对后续过程有负面影响，则该操作是有益的，可以看成是某种偏置无关操作；如果原始特征值有特殊意义，比如稀疏性，该操作可能会破坏其稀疏性。

除以一个统计量可以看成在坐标轴方向上对特征进行缩放，用于降低特征尺度的影响，可以看成是某种尺度无关操作。缩放可以使用最大值最小值间的跨度，也可以使用标准差（到中心点的平均距离），前者对outliers敏感，outliers对后者影响与outliers数量和数据集大小有关，outliers越少数据集越大影响越小。

除以长度相当于把长度归一化，把所有样本映射到单位球上，可以看成是某种长度无关操作，比如，词频特征要移除文章长度的影响，图像处理中某些特征要移除光照强度的影响，以及方便计算余弦距离或内积相似度等。

归一化/标准化的目的是为了获得某种“无关性”——偏置无关、尺度无关、长度无关……当归一化/标准化方法背后的物理意义和几何含义与当前问题的需要相契合时，其对解决该问题就有正向作用，反之，就会起反作用。所以，“何时选择何种方法”取决于待解决的问题，即problem-dependent。

什么时候需要特征缩放

（1）涉及或隐含距离计算时：，比如K-means、KNN、PCA、SVM等

• zero-mean一般可以增加样本间余弦距离或者内积结果的差异，区分力更强，假设数据集集中分布在第一象限遥远的右上角，将其平移到原点处，可以想象样本间余弦距离的差异被放大了。在模版匹配中，zero-mean可以明显提高响应结果的区分度。

• 就欧式距离而言，增大某个特征的尺度，相当于增加了其在距离计算中的权重，如果有明确的先验知识表明某个特征很重要，那么适当增加其权重可能有正向效果，但如果没有这样的先验，或者目的就是想知道哪些特征更重要，那么就需要先feature scaling，对各维特征等而视之。

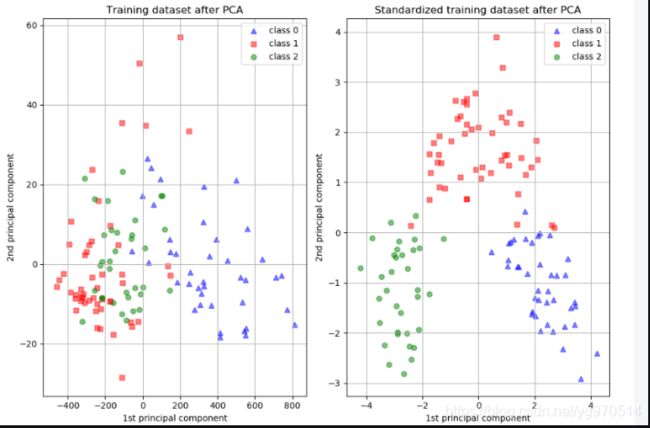
• 增大尺度的同时也增大了该特征维度上的方差，PCA算法倾向于关注方差较大的特征所在的坐标轴方向，其他特征可能会被忽视，因此，在PCA前做Standardization效果可能更好，如下图所示，图片来自scikit learn-Importance of Feature Scaling

• 损失函数中含有正则项时，一般需要feature scaling：对于线性模型y=w_x+by=w_x+b而言，xx的任何线性变换（平移、放缩），都可以被w和b“吸收”掉，理论上，不会影响模型的拟合能力。但是，如果损失函数中含有正则项，如λ||w||2λ||w||2，λλ为超参数，其对w的每一个参数施加同样的惩罚，但对于某一维特征xi而言，其scale越大，系数w_i越小，其在正则项中的比重就会变小，相当于对w_i惩罚变小，即损失函数会相对忽视那些scale增大的特征，这并不合理，所以需要feature scaling，使损失函数平等看待每一维特征。
• 梯度下降算法，需要feature scaling
• 对于传统的神经网络，对输入做feature scaling也很重要，因为采用sigmoid等有饱和区的激活函数，如果输入分布范围很广，参数初始化时没有适配好，很容易直接陷入饱和区，导致梯度消失，所以，需要对输入做Standardization或映射到0,1、−1,1，配合精心设计的参数初始化方法，对值域进行控制。但自从有了Batch Normalization，每次线性变换改变特征分布后，都会重新进行Normalization，似乎可以不太需要对网络的输入进行featurescaling了？但习惯上还是会做feature scaling。

什么时候不需要归一化：

与距离计算无关的概率模型，不需要feature scaling，比如Naive Bayes；

与距离计算无关的基于树的模型，不需要feature scaling，比如决策树、随机森林等，树中节点的选择只关注当前特征在哪里切分对分类更好，即只在意特征内部的相对大小，而与特征间的相对大小无关。