Minimax AI 算法在井字游戏(或 Noughts and Crosses)游戏中的实现
GitHub - Cledersonbc/tic-tac-toe-minimax: Minimax is a AI algorithm.
井字游戏
Minimax AI 算法在井字游戏(或 Noughts and Crosses)游戏中的实现。试试看:井字游戏 - Minimax
介绍
为了使用 AI 解决游戏,我们将介绍博弈树的概念,然后是极小极大算法。博弈的不同状态由博弈树中的节点表示,与上述规划问题非常相似。这个想法只是略有不同。在游戏树中,节点按照每个玩家在游戏中的轮次排列,因此树的“根”节点(通常描绘在图的顶部)是游戏中的开始位置。在井字游戏中,这将是尚未播放 Xs 或 Os 的空网格。在根下,在第二层,有可能由第一个玩家的移动产生的状态,无论是 X 还是 O。我们称这些节点为根节点的“子节点”。
第二层上的每个节点,将进一步具有作为其子节点的状态,该状态可以通过对方玩家的移动到达。这将逐级继续,直到达到游戏结束的状态。在 tic-tac-toe 中,这意味着任一玩家获得三线并获胜,或者棋盘已满并且游戏以平局结束。
什么是极小极大?
Minimax 是一种应用于两人游戏的人工智能,例如井字游戏、跳棋、国际象棋和围棋。这种游戏被称为零和游戏,因为在数学表示中:一个玩家赢(+1),另一个玩家输(-1)或任何人都不赢(0)。
它是如何工作的?
该算法递归地搜索导致Max玩家获胜或不输(平局)的最佳走法。它考虑游戏的当前状态和该状态下的可用移动,然后对于它所玩的每个有效移动(交替min和max),直到找到最终状态(赢、平或输)。
了解算法
该算法由 Algorithms in a Nutshell (George Heineman; Gary Pollice; Stanley Selkow, 2009) 中文版算法技术手册(原书第2版)一书研究。伪代码(改编):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end现在我们将使用 Python 实现来查看此伪代码的每个部分。Python 实现在此存储库中可用。首先,考虑一下:
板 = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
最大值 = +1
最小值 = -1
MAX 可能是 X 或 O,而 MIN 可能是 O 或 X,无论如何。板是 3x3。
def minimax(state, depth, player):
- state : 井字游戏中的当前棋盘(节点)
- depth : 游戏树中节点的索引
- player : 可能是MAX玩家或MIN玩家
if player == MAX:
return [-1, -1, -infinity]
else:
return [-1, -1, +infinity]
两名球员都从你最差的成绩开始。如果玩家是MAX,它的分数是-infinity。否则,如果玩家是 MIN,它的分数是 +infinity。注意: infinity是 inf 的别名(来自 Python 中的数学模块)。
棋盘上最好的棋步是 [-1, -1](行和列)。
if depth == 0 or game_over(state):
score = evaluate(state)
return score
如果深度等于 0,则棋盘没有新的空单元可玩。或者,如果玩家获胜,则游戏以 MAX 或 MIN 结束。因此将返回该状态的分数。
- 如果 MAX 赢了:返回 +1
- 如果 MIN 赢了:返回 -1
- 否则:返回 0(平局)
现在我们将看到包含递归的这段代码的主要部分。
for cell in empty_cells(state):
x, y = cell[0], cell[1]
state[x][y] = player
score = minimax(state, depth - 1, -player)
state[x][y] = 0
score[0], score[1] = x, y
对于每个有效的移动(空单元格):
- x:接收单元格行索引
- y:接收单元格列索引
- state[x][y]:就像 board[available_row][available_col] 接收 MAX 或 MIN 玩家
- score = minimax(状态,深度 - 1,-player):
- state: 是递归中的当前棋盘;
- depth -1:下一个状态的索引;
- -player:如果玩家是 MAX (+1) 将是 MIN (-1),反之亦然。
棋盘上的移动(+1 或 -1)被撤消,行、列被收集。
下一步是将分数与最佳分数进行比较。
if player == MAX:
if score[2] > best[2]:
best = score
else:
if score[2] < best[2]:
best = score
对于 MAX 玩家,将获得更高的分数。对于 MIN 玩家,将获得较低的分数。最后,最好的举动被退回。最终算法:
def minimax(state, depth, player):
if player == MAX:
best = [-1, -1, -infinity]
else:
best = [-1, -1, +infinity]
if depth == 0 or game_over(state):
score = evaluate(state)
return [-1, -1, score]
for cell in empty_cells(state):
x, y = cell[0], cell[1]
state[x][y] = player
score = minimax(state, depth - 1, -player)
state[x][y] = 0
score[0], score[1] = x, y
if player == MAX:
if score[2] > best[2]:
best = score
else:
if score[2] < best[2]:
best = score
return best
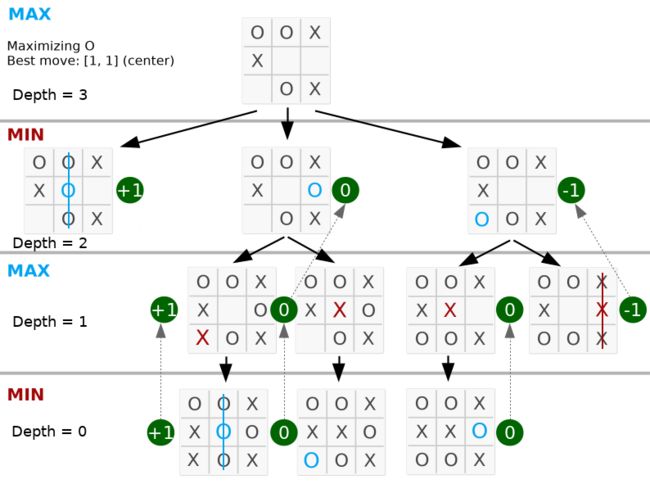
游戏树
下面,最好的移动在中间,因为最大值在左边的第二个节点上。
看看深度是否等于板上的有效移动。完整的代码在py_version/中可用。
简化游戏树:
那棵树有 11 个节点。完整的游戏树有 549.946 个节点!您可以测试它在程序中放置一个静态全局变量,并为每轮的每个 minimax 函数调用递增它。
在更复杂的游戏中,例如国际象棋,很难搜索整个游戏树。然而,Alpha-beta Pruning 是极小极大算法的一种优化方法,它允许我们忽略搜索树中的一些分支,因为他在搜索中剪掉了不相关的节点(子树)。有关更多信息,请参阅:
- 书:George T. Heineman;加里·波利斯;斯坦利·塞尔科夫。算法简而言之。奥莱利,2009 年。
- 维基百科:https ://en.wikipedia.org/wiki/Minimax
- 南洋理工大学:https ://www.ntu.edu.sg/home/ehchua/programming/java/JavaGame_TicTacToe_AI.html