机器学习之手写字体（digits）识别——利用sklearn实现

**

机器学习之手写字体（digits）识别——利用sklearn实现

**

1实验目的

为了进一步地掌握建立机器学习模型的流程,理解机器学习的基本概念,此次实验针对sklearn自带的digits数据集（手写字体识别数据集）进行分类预测。
在此次实验中,我选用了KNN、MLP、Random Forest、Adaboost、SVM、Decision Tree、Logistic Regression这七种机器学习算法模型进行手写字体的识别。
本次项目的实验环境为pycharm + python3.9，经测试，各种算法模型在安装了python3.9的jupyter notebook中均可以正常运行

2实验过程

2.1 查看数据集

首先，将sklearn库中的数据集导入到项目中，其中X为1797*64的二维数组，代表数据集中1797个样本，每一个样本图片均是一维向量，特征维度为64，每个像素点代表1维的特征，其取值范围为0-16；y为样本所对应的标签值，共有10个类别，其取值范围为0-9中的任意一个数字。将数据集导入项目中的代码如下所示：

from sklearn.datasets import load_digits
digits = load_digits()
X = digits.data
y = digits.target

如果要可视化查看数据集，则需要将样本图片转换为二维，然后借助matplotlib包实现，以数据集中的第1796个样本9为例，具体的实现方式，如下所示：

import matplotlib.pyplot as plt
def show(image):
    test = image.reshape((8, 8))  # 从一维变为二维，这样才能被显示
    print(test.shape)  # 查看是否是二维数组
    plt.imshow(test, cmap=plt.cm.gray)  # 显示灰色图像
plt.show()
if __name__ == '__main__':
    show(X[1795])

数字9图片如下图所示：

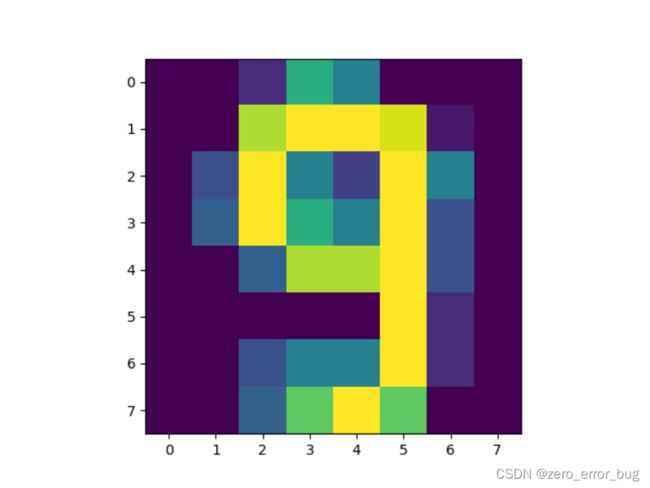
考虑到在后续算法模型的建立过程中，需要用到的样本是一维向量，故show()函数只用来对数据集的查看和检验，并不将数据集全部进行转换。

2.2 数据清理

数据集的预处理主要分为两部分，分别是特征标准化和特征降维。

2.2.1特征标准化

调用sklearn中对数据进行标准化的函数处理样本X，特征标准化的过程如下：

from sklearn.preprocessing import StandardScaler
def standard_demo(data):
    transfer = StandardScaler()
    data_new = transfer.fit_transform(data)
    print(data_new)
    return data_newif __name__ == '__main__':
X_new = standard_demo(X)
if __name__ == '__main__':
    X_new = standard_demo(X)

2.2.2特征降维

考虑到样本中的特征维度为64维，可能包含一些相近的维度或噪音等，这些维度会影响算法模型的性能，容易产生过拟合等现象，因此，在数据清理时，需要对样本进行特征降维。实现代码如下：

from sklearn.decomposition import PCA
def pca_demo(data):
    transfer = PCA(n_components=0.92)
    data_new = transfer.fit_transform(data)
    print(data_new)
    return data_newif __name__ == '__main__':
X_new = pca_demo(X_new)
if __name__ == '__main__':
    X_new = pca_demo(X_new)

其中，在进行降维的过程中，保留原本数据集大小的百分比对与算法的准确率具有较大的影响，此次实验中，以KNN算法为例，从84%一直到96%，实验PCA降维之后算法的准确率，最终实验得到的结果如下表所示：

Percentage(%)	84	85	86	87	88	89	90	91	92	93	94	95	96
Accuracy	0.96	0.96	0.97	0.97	0.96	0.97	0.97	0.97	0.98	0.97	0.97	0.97	0.97

由于这是在调参之后测出的结果，所以在四舍五入之后，它们之间并没有很明显的差距，但是在保留原数据集92%的情况下，准确率依然很明显，故此次实验的降维参数n_components=0.92，特征维度降为34维，由此可见，数据集中的确存在大量的噪音或比较接近的特征维度。

2.3 机器学习建模

数据集已经准备好了，下一步就是建立机器学习算法模型，对模型进行训练。

2.3.1 KNN算法

我第一个选择的算法模型为KNN算法，因为它的原理比较简单，对于这种小数据集来说，理论上看它应该会有不错的表现，模型构建如下：

from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
def knn_demo(data, label):
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, label, random_state=6)
    # 训练模型
    estimate = KNeighborsClassifier(n_neighbors=10)
estimate.fit(X_train, y_train)  # 模型构建好了
if __name__ == '__main__':
    knn_demo(X_new, y)

在模型构建之前，需要先调用train_test_split函数对数据集进行划分，这里采用了数据集默认的划分方式，即训练集：测试集=0.75：0.25，调用KNeighborsClassifier函数构建模型，参数n_neighbors=10代表对每一个样本点进行分类时，都要找到离他最近的10个“邻居”，算法准确率为0.98

2.3.2 MLP算法

第二个算法模型为人工神经网络中的全连接网络，即多层感知机算法(MLP)，模型构建如下：

from sklearn.neural_network import MLPClassifier
def MLP_demo(data, label):
    # 对标签进行独热编码
    label = code_demo(data, label)
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, label, random_state=6)
    # 训练模型
    estimate = MLPClassifier(hidden_layer_sizes=(100,), activation='relu', solver='lbfgs', learning_rate_init=0.001, max_iter=2000)
estimate.fit(X_train, y_train)  # 模型构建好了
def code_demo(data, label):
    numFiles = len(data)
    hwLabels = np.zeros([numFiles, 10]) #用于存放对应的one-hot标签
    for i in range(numFiles):  # 遍历所有的样本
        digit = label[i]
        hwLabels[i][digit] = 1.0  # 将对应的one-hot标签置1
    return hwLabels
if __name__ == '__main__':
MLP_demo(X_new, y)

此次实验中，由于MLP的参数比较多，且对算法的性能影响较大，因此需要对模型的各种参数进行调节，以寻求最优越的分类模型，分别对模型中的隐藏层、激活函数、权重优化器、学习率以及迭代次数进行调节。
隐藏层：

Hidden layer and number of
neurons	(100,)	(1000,)	(100,100)	(1000,1000)	(1000,100)
Accuracy	0.94	0.94	0.93	0.95	0.94

从表中可以看到，上述隐藏层的变化对于模型性能的影响很小，随着隐藏层及神经元的增加，对于硬件设施的要求也高，而且运行效率低，因此，为了一点性能的提升，加大硬件设施的负担，性价比并不高，因此本实验最终选择了一层隐藏层，神经元数量为100，也可以达到较为不错的效果。
激活函数：

Activation	relu	identity	logistic	tanh
Accuracy	0.94	0.88	0.93	0.92

从表中可以看出，relu激活函数在此次实验中具有较为不错的表现，可以提升模型的准确率，因此本算法模型，最终选用relu作为激活函数。
权重优化器：

solver	lbfgs	Adam	sgd 
Accuracy	0.94	0.93	0.89

从表中可以看出，lbfgs权重优化器更适合此次手写字体数据集的识别，因此，本算法模型选择lbfgs作为权重函数优化器。
学习率：

learning_rate_init	0.001	0.0001	0.00001 
Accuracy	0.94	0.93	0.93

从表中可以看出，学习率为0.001时不仅算法模型的准确率高，对硬件设施的负担也较小，故此次MLP模型选择0.001为学习率参数。
迭代次数：

max_iter	200	2000	20000
Accuracy	0.92	0.93	0.93

从性价比方面考虑，选择2000作为最大迭代次数更为优越。
故在对比MLP的一系列参数之后，构建模型的算法准确率为0.94；但是如果不对标签数据进行独热编码，使用MLP模型可以得到0.96的准确率，这也是此次实验的一处疑惑，后文会在总结时进一步分析原因。

2.3.3 RandomForest算法

随机森林是集成学习算法bagging系列的代表算法之一，它使几个弱监督分类器集中起来，可以拥有强监督器的分类能力，而随机森林属于并行式的分类算法，在多分类问题上采用各个分类器投票表决的模式，因此，理论上来看，它在此次数据集的识别上，应该会有比较不错的表现。

from sklearn.ensemble import RandomForestClassifier
def forest_demo(data, label):
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, label, random_state=6)
    # 训练模型
    estimate=RandomForestClassifier(n_estimators=100,criterion='gini', max_depth=20000)
estimate.fit(X_train, y_train)  # 模型构建好了
if __name__ == '__main__':
forest_demo(X_new, y)

该模型的性能主要收森林中树木的数量以及节点分裂函数的影响，对这两个参数进行调整，如下所示。

n_estimators	10	100	1000 	
Accuracy	0.93	0.95	0.95 
criterion	gini	entropy	None	
Accuracy	0.95	0.94	None 
max_depth	200	2000	20000
Accuracy	0.95	0.95	0.96

故随机森林模型的最终参数确定之后，模型准确率达0.96。

2.3.4 Adaboost算法

Adaboost是集成学习算法boost系列的代表算法之一，与随机森林算法不同的是，它是一种串行式的学习算法，在二分类问题上具有极大的优越性，但在多分类问题上，还需要进一步的测试，模型构建如下：

from sklearn.ensemble import AdaBoostClassifier
def Adab_demo(data, label):
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, label, random_state=6)
    # 训练模型
    estimate=AdaBoostClassifier(n_estimators=100, learning_rate=0.1 )
    estimate.fit(X_train, y_train)  # 模型构建好了
if __name__ == '__main__':
Adab_demo(X_new, y)

该模型的性能主要收森林中树木的数量以及学习率的影响，对这两个参数进行调整，如下所示。

n_estimators	10	    100	    1000
Accuracy	   0.34 	0.63	0.56
learning_rate  0.01	    0.1	     1
Accuracy	   0.63	    0.50	0.48

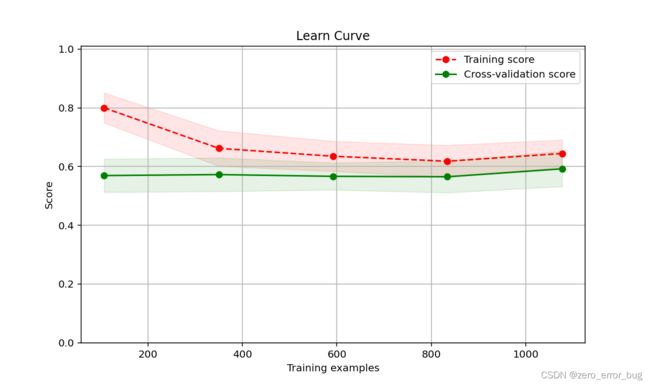
由上表可以看出，Adaboost算法模型在此次实验中的表现比较差，不过也可以理解，根据没有免费的午餐定理，Adaboost在二分类问题上的优越性也决定了它在多分类问题上的局限性，该算法不太适合处理多分类问题。

2.3.5 SVM算法

SVM算法在处理二分类问题上具有比较优越的性能，其在多分类问题上的表现还需进一步的测试，算法构建如下：

from sklearn import svm
def svm_demo(data, label):
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, label, random_state=6)
    # 训练模型
    estimate = svm.SVC()
estimate.fit(X_train, y_train)  # 模型构建好了
if __name__ == '__main__':
svm_demo(X_new, y)

SVM的默认多分类方法为ovr，即一类对另一类，把多分类问题转换为二分类问题，最后再通过投决进行分类。虽然在我看来，这样做会使得数据集分布不均衡，进而影响到分类模型的性能，而且由于svm在二分类上的优越性，我认为它在多分类上应该不会有很好的表现，可是加上svm在多分类问题上依然有着很强悍的性能表现，如下所示：
random_state 默认 6 2
Accuracy 0.97 0.97 0.96
SVM不愧是影响了半个世纪的机器学习算法，它不仅运行效率高，而且在二分类和多分类问题上都有着不俗的表现。

2.3.6 Dicisiontree算法

决策树模型的构建如下所示：

from sklearn.tree import DecisionTreeClassifier
def Tree_demo(data, label):
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, label, random_state=6)
    # 训练模型
    estimate=DecisionTreeClassifier(criterion='entropy',splitter='best', max_depth=200)
estimate.fit(X_train, y_train)  # 模型构建好了
if __name__ == '__main__':
Tree_demo(X_new, y)    # 训练模型

该模型的性能主要受森林中节点分裂函数、树的最大深度、节点拆分策略的影响，对这几个参数进行调整，如下所示。

criterion	gini	entropy	None
Accuracy	0.81	0.84	None
splitter	best	random	None
Accuracy	0.81	0.80	None
max_depth	100	200	500
Accuracy	0.82	0.81	0.81

故该模型的最终参数确定之后，模型准确率为0.84

2.3.7 Logistic Regression算法

逻辑回归算法是处理分类问题的算法，尤其在处理二分类问题方面表现不错，在处理多分类问题主要有两种方式，一种是’ovr’方法，另一种是’multinomial’方法。模型构建如下所示：

from sklearn.linear_model import LogisticRegression
def Logistic_demo(data, label):
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, label, random_state=6)
    # 训练模型
    estimate = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=10000)  # 可以选择多分类方法 ovr 和 multinomial
estimate.fit(X_train, y_train)  # 模型构建好了
if __name__ == '__main__':
Logistic_demo(X_new, y)

该模型主要受采用何种多分类方法以及权重优化器的影响，对比结果如下表所示：

multinomial	sag	Accuracy
	saga	0.94
	lbfgs	0.94
	newton-cg	0.94
ovr	sag	0.94
	saga	0.94
	lbfgs	0.93
	newton-cg	0.93

从运行时长以及算法准确率两个方面综合考虑，此模型应当选择multinational方法处理手写字体识别问题，优化器选择’lbfgs’。

2.4 模型的参数确定

经过对上述机器学习算法的讨论以及各种参数的调整，最终所确定的机器学习算法参数以及在测试集的准确率如下所示：

Model	None	None	None	None	None	Accuracy
KNN	n_neighbors=10	None	None	None	None	0.98
MLP	hidden_layer_sizes=(100,)	activation='relu'	solver='lbfgs'	learning_rate_init=0.001	max_iter=2000	0.96
RandomForest	n_estimators=100	criterion='gini'	max_depth=20000	None	None	0.96
Adaboost	n_estimators=100	earning_rate=0.1	None	None	None	0.63
SVM	decision_function_shape='ovr'	kernel='rbf'	None	None	None	0.97
Dicisiontree	criterion='entropy'	splitter='best',	max_depth=200	None	None	0.84
Logistic Regression	multi_class='multinomial'	solver='lbfgs'	max_iter=10000	None	None	0.94

从表中可以看出，SVM和KNN算法模型在处理该手写数字识别问题数据集时，性能比较优越；而Adaboost算法则不能很好地处理这种多分类问题，在测试集上地准确率较低；决策树算法由于本身的特点，在训练集上可能出现了过拟合的现象，导致测试集上的准确率并不是很突出，调整参数之后，准确率依然达不到0.90以上；而其他各类算法的准确率均能保持在90%以上。

2.5学习曲线的绘制

学习曲线指的是，随着训练样本的增加，模型在训练集上的准确率与交叉验证得到的准确率的变化，画出算法模型各自的学习曲线，实现代码如下：

 cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)  # 10折交叉验证
    fig, ax = plt.subplots(1, 1, figsize=(10, 6), dpi=144)
    plot_learning_curve(ax, estimate, "Learn Curve",
                        X_train, y_train, ylim=(0.0, 1.01), cv=cv)
    plt.show()

此次画图中，采用的是10折交叉验证的方法，训练集与验证集的比例划分为0.8：0.2，最终画出的图像如下所示。
KNN Learning Curve

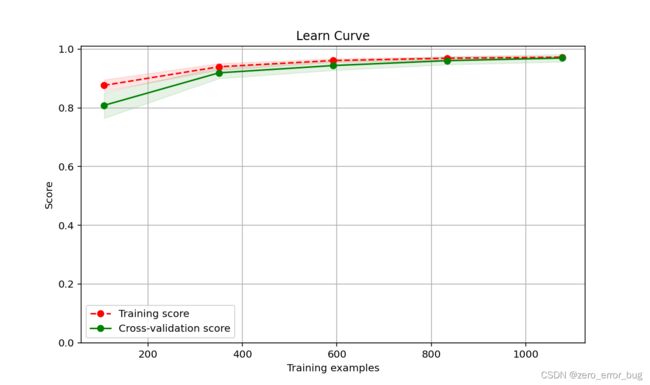
MLP Learning Curve

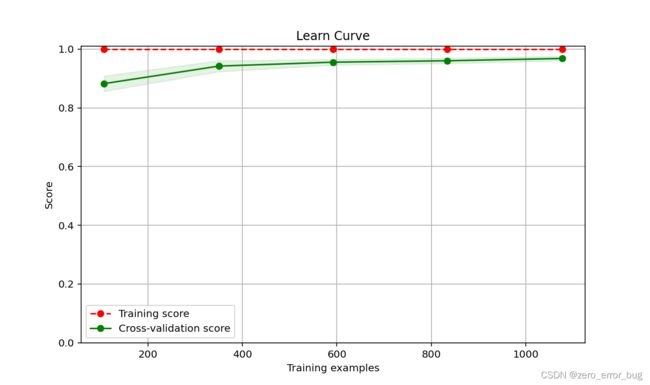
RandomForest Learning Curve

Adaboost Learning Curve

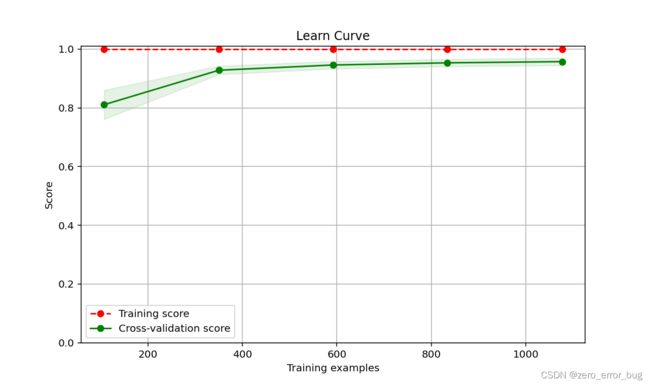
SVM Learning Curve

DecisionTree Learning Curve

LogisticRegression Learning Curve

从学习曲线也可以直观的看出，KNN与SVM的性能更为优越，决策树存在过拟合现象，Adaboost算法存在欠拟合现象，其他各类算法表现较为良好。

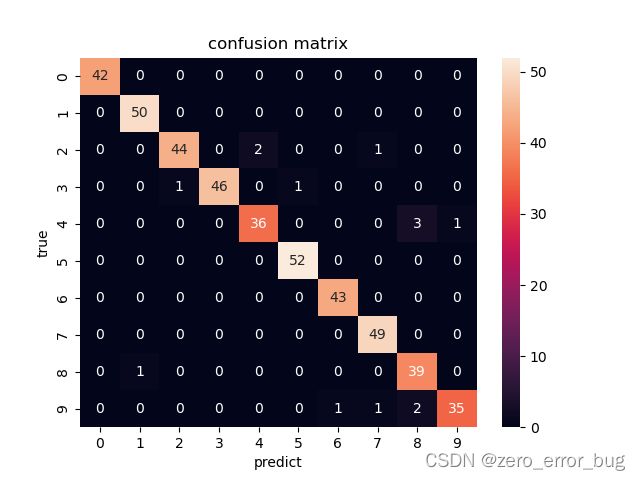
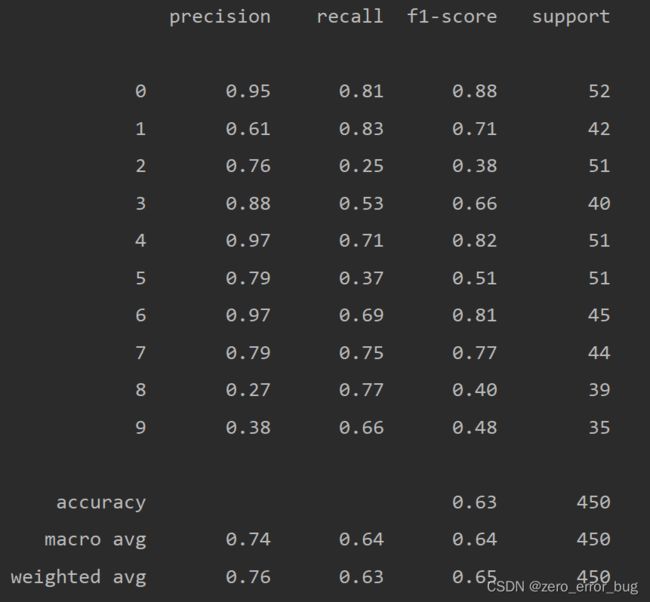
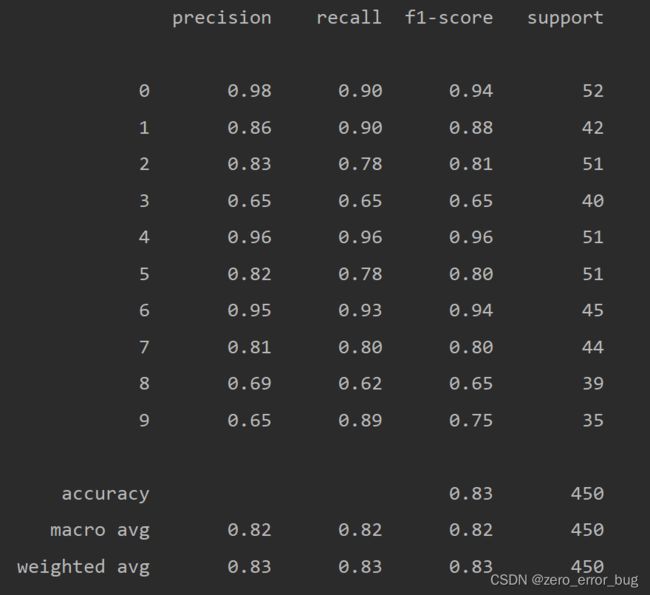
2.6模型性能的衡量

根据上述结果已经可以确定哪些模型在此实验中具有更好的表现，哪些模型不太适合此次的多分类实验，但是为了更进一步的表达算法在样本上的估计率以及针对每一类别，它们的预测效果如何。在本实验中，采用可视化的混淆矩阵和每一类别的精确率与召回率计算结果继续对实验结果进行分析。可视化混淆矩阵以及计算精确率与召回率的实现方式如下：

from sklearn.metrics import confusion_matrix
import seaborn as sn

混淆矩阵

cm = confusion_matrix(y_test, y_predict)
print(cm)
# 可视化显示混淆矩阵
# annot = True 显示数字 ，fmt参数不使用科学计数法进行显示
ax = sn.heatmap(cm, annot=True, fmt='.20g')
ax.set_title('confusion matrix')  # 标题
ax.set_xlabel('predict')  # x轴
ax.set_ylabel('true')  # y轴
plt.show()

计算精确率与召回率

report = classification_report(y_test, y_predict, labels=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9], target_names=['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'])
print(report)

在画混淆矩阵时，没有借助matplotlib实现，而是用seaborn库实现，它是对matplotlib进行二次封装实现的，操作更为简单。在计算精确率与召回率的过程中，将数字0—9分为了10个类别，更加形象与直观。各个算法的混淆矩阵以及精确率和召回率的计算结果如下所示：
混淆矩阵：
KNN Learning Curve

MLP Learning Curve

RandomForest Learning Curve

Adaboost Learning Curve

SVM Learning Curve

DecisionTree Learning Curve

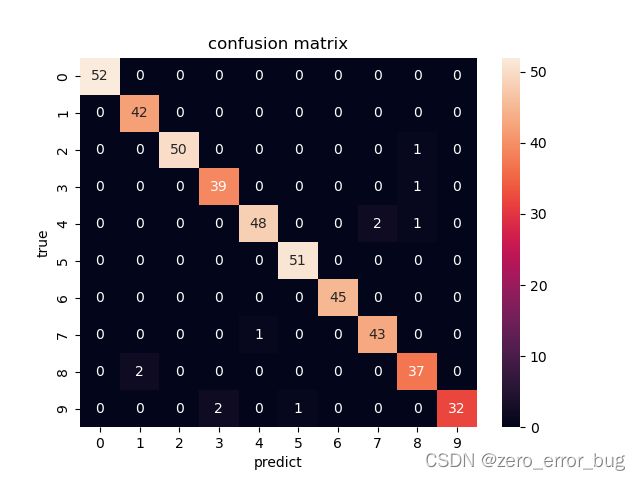
LogisticRegression Learning Curve

精确率与召回率计算：
KNN Learning Curve

MLP Learning Curve

RandomForest Learning Curve

Adaboost Learning Curve

SVM Learning Curve

DecisionTree Learning Curve

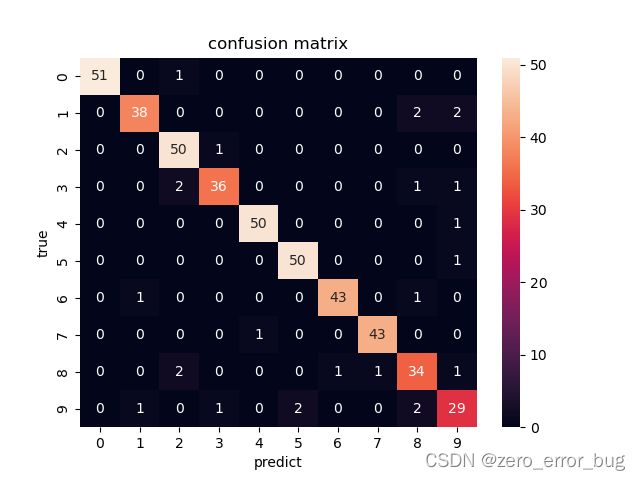
LogisticRegression Learning Curve

从上述结果中不仅可以看出算法整体的准确率，还可以观察到算法对各个类别的识别率，上述结果均是在调参之后得到的数据，由以上信息，我们可以依据这七种算法模型在数据集上的表现进行排序，排序结果如下：

根据天下没有免费的午餐定理，上述排序仅限于在该实验的手写数字识别问题上，如果数据集发生变化，上述结论可能也会发生变化，甚至，让不同的人来进行调参，他们得到的结果也可能不同，毕竟参数有时候对于算法模型的影响是巨大的。总之，在此次实验中，构建的七种模型中，KNN与SVM是最令人满意的。

3实验问题分析

1.此次实验中我遇到的第一个问题是如何让样本以图片的形式显示出来，在数据集里拿到的数据是1797*64的二维数据，每一个样本均是一维的向量，在网上查阅相关问题之后发现，imshow函数的输入必须是二维的，然后我又找到了reshape函数，该函数可以对向量进行转换，我利用它将一维向量转换为了二维向量，最终可以成功的显示数据集中的图片。
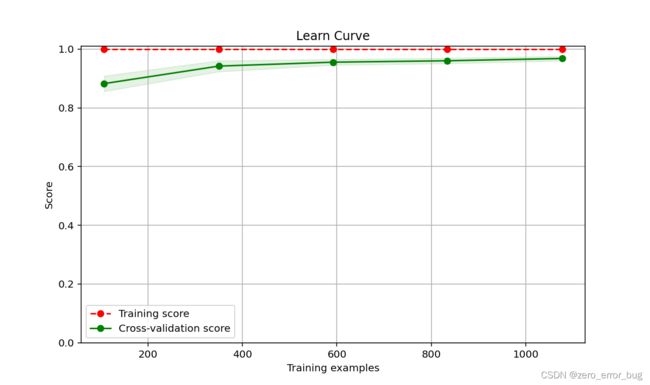
2.在MLP算法模型的建立过程中，最开始我没有想到对标签进行独热编码变换，直接利用数据集分割函数分割数据集，然后用模型训练它们，最终得到了0.96的准确率。构建完MLP模型之后，我在想如果用独热编码会不会提升模型的性能呢，于是我将每一个标签都利用独热编码的规则，转换成了10维的行向量，然后重新构建MLP模型，结果却发现准确率居然不升反降，这个问题困扰了我好久，在网上也搜集了很多资料，都没有相关的介绍，直到我构建完七个模型之后，我大概明白了出现这种情况的原因。其实，我认为在此次实验中，对不对标签进行独热编码都是可以的，而且独热编码的确有很大的优越性，在计算方面可能会更加简单，但是MLP是一个全连接的网络，这个模型本身的复杂度已经很高了，我构建的模型更是一个含有100层神经元隐藏层的MLP模型，而我们的数据集总共只有1797个样本，在划分数据集之后，训练集就只有1348个样本左右了，所以，我推测不是独热编码的原因使得准确率下降，而是因为算法模型比较复杂，数据集比较少，该算法在训练集上出现了过拟合导致的，于是，我重新对比了一下对标签进行独热编码和不对标签进行独热编码的结果，如下图所示。从图中可以直观的看出，在对标签数据进行独热编码的情况下，模型确实出现了一定程度的过拟合，由此可以验证我上述的猜想是正确的。
不进行独热编码

进行独热编码

3.在进行实验之前，对于多分类问题，我能想到的解决办法只有KNN与MLP算法，因为在我看来SVM，LogisticRegerssion等算法都是用来处理二分类的，虽然也可以处理多分类问题，但是要构建多个分类器或者对数据集划分等等，操作起来还是很困难的，但是当我真正去尝试的时候，我发现SVM、RandomForest、LogisticRegression等算法对于多分类问题依然可以得到一个而很好的结果。我就非常好奇，然后在网上查阅很多文章，又打开了算法模型的内部函数看了一遍之后，我终于明白这是什么原因了。原来，sklearn库的工作人员也想到了这些问题，SVM和LogisticRegression等算法确实需要通过一对多或一类对另一类的方法实现多分类，但这些都不需要我自己去动手重新搭建，在这些算法模型的类中早就设定好了这些参数，如果你想要实现一个多分类问题，只需要去认为改变这些参数就可以了，于是，我就把这七种算法都尝试了一遍，发现大多算法都可以取得不错的性能。
4.在实验中的几种机器学习算法中，准确率大都可以保持在90%或80%以上，唯有Adaboost算法的准确率在63%，在我调整了学习率和分类器的个数之后还是没有明显的变化，其余六种算法模型在默认的情况下，准确率都在90%和80%以上，而Adaboost算法在默认情况下只有30%多，在经过调参之后，准确率上升到63%，但这显然要远远低于其他算法。查阅相关资料后发现，Adaboost作为一种并行式的算法，是处理二分类问题的利器，但在多分类问题上可能不是很理想，还有一个原因，可能由于数据集的样本数不多，导致该算法出现欠拟合的现象。

4实验心得

在此次实验之前，我在机器学习算法方面的学习，理论知识要多于实践的，但是很多细节我都没有仔细的思考过，在编程的环节中，我不断的实践各种算法，对它们的参数进行调整，以往被我忽略的一些问题，我也能重新思考它们，这是理论学习不能带给我的。而且在编程环节的练习，我认为它比理论的教学更有趣一点，不像推导公式那样枯燥，有时候推导一遍之后又忘了，但是当我看到自己构建的模型可以得到一个不错的准确率时，心里还是会有一种小小的成就感的，当然，如果没有理论方面的学习，我可能连实践的心思都没有。之前我自学过一段时间的机器去学习，但是理论知识有点缺乏，所以没有坚持下来，而这学期跟着老师系统的学习一遍，在理论上，我还是有所收获的，几个著名的机器学习算法也不是完全不懂了，在编程上也可以更好的入手与学习了。这门课的学习令我受益匪浅。

5源程序

此次实验用pycharm实现，移植到jupyter里面可正常运行，两种实现方式均打包在下面的压缩文件里了，有需要的可自取（实验环境为pycharm + python3.9）

链接：https://pan.baidu.com/s/1PWQ4vaFm16k-_rBxN4WtCg?pwd=0000 
提取码：0000 
--来自百度网盘超级会员V4的分享