《SCA-CNN：Spatial and Channel-wise Attention in Convolutional Networks for Image Captioning》论文笔记

1. 前言

视觉上的attention已经被成功运用在了结构预测任务中。例如，visual captioning与question answering。现有的视觉attention模型都是基于空间的，既是重新加权最后一个卷积层的feature map。其原理如下图所示，但是这样的或许并不能会很好符合attention的机制。

文章中指出，基于CNN的原理，其所提取的feature map具有spatial、channel-wise（semantic）、multi-layer的属性。但现有的一些image caption方法主要考虑spatial的属性，其中运用的attention机制也都是spatially attentive weight。因而在此基础上论文提出，充分利用CNN以上三个属性来进行image caption的任务，提出利用spatial、channel-wise(semantic)和multi-layer结合的属性进行attention机制的应用，相互影响，相互促进，有很好的效果，取名SCA-CNN。

2. SCA-CNN网络

2.1 网络结构

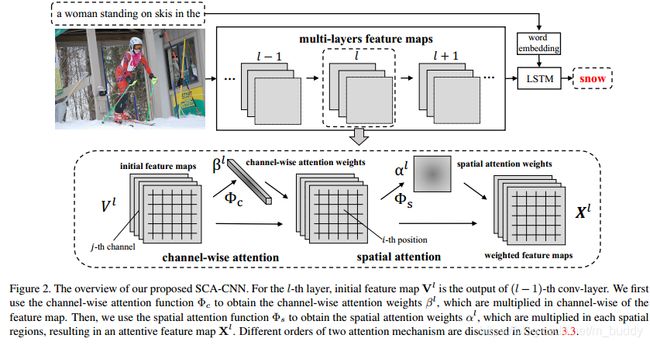
其网络结构如上图，可以看到在每层的feature map上先后做了channel-wise与spatial的attention，里面根据卷积feature map中channel与spatial的特性对其进行加权组合。对于前面两种：spatial、channel-wise的attention比较容易理解，那么如何将其扩展到multi-layer上呢？论文中是使用模块堆叠实现的。也正如上面结构中的$l-1$、$l$、$l+1$特征层。了解了网络的结构，那么接下来就看一下其内部是怎么实现这些的。

2.2 spatial attention

首先，来看一下整个attention的更新方式，其更新方式如下：

其中，$X^{l-1}$是卷积特征层；$V^l$可以看作是SCA-CNN的模块运算中间变量；$h_{t-1}$是$d$维度的上一时刻的LSTM层hidden输出；${\gamma }^l$是attention之后的权重；函数$f$也就是按照权重使得卷积重分布了。最后通过LSTM层得到图片的caption：

其中，$y_t$就是最后输出的图片描述单词了。那么回到正题，spatial中的权重分布是怎么计算得到的呢？也就是下面要求的东西：

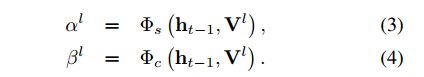
对于spatial上的权重计算（也就是上面的公式3）的计算是通过下面这个算子实现的：
$$a=tanh((W_{s}V+b_s)\oplus W_{hs}{h}_{t-1})$$
$$\alpha =softmax(W_{i}a+b_i)$$

其中，参数$a$就是attention中的score函数；$V=[v_1,v_2,\dots ,v_m]$是向量，其中每个元素的长度是$C$（也就是feature map中的channel数量），$m=W\ast H$（feature map的宽高乘积）；$W_s\in R^{k\ast C},W_{hs}\in R^{k\ast d},W_i\in R^k$。$\oplus$代表的是向量与矩阵的运算。

2.3 channel-wise attention

channel-wise上的attention与spatial上的是类似的。首先，将feature map进行reshape操作得到向量$U=[u_1,u_2,\dots ,u_C]$，它的元素个数是channel的数目，每个元素的维度是$W\ast H$。之后呢，再把每个元素进行average Pooling得到向量$v=[v_1,v_2,\dots ,v_C]$。因而最后的权重计算被表述为：

在论文中还讨论了spatial与channel-wise attention先后顺序的区别，其实验结果为：

结论就是channel-wise在前面要好一些。这篇文章的大体内容如上所述，文章其性能全面领先与其他state-of-the-art，主要原因就是其充分利用CNN的三种重要特性，而这些特性对语义的理解往往又很有效，所以得到较好的效果。这个方案给了我们很多认识，多种有效手段集合，可以获得很好的效果，但这对计算资源有很高的要求。