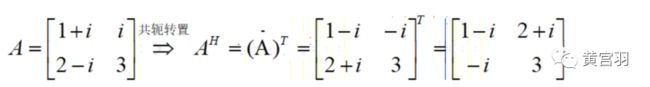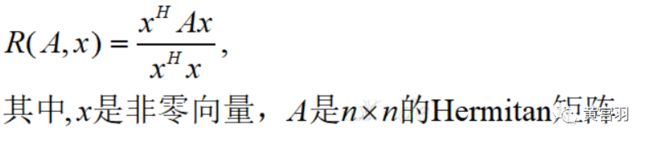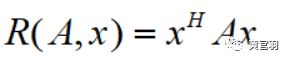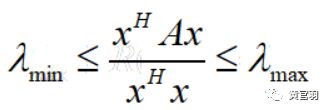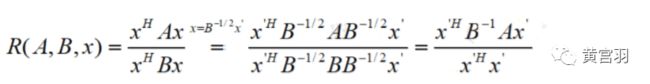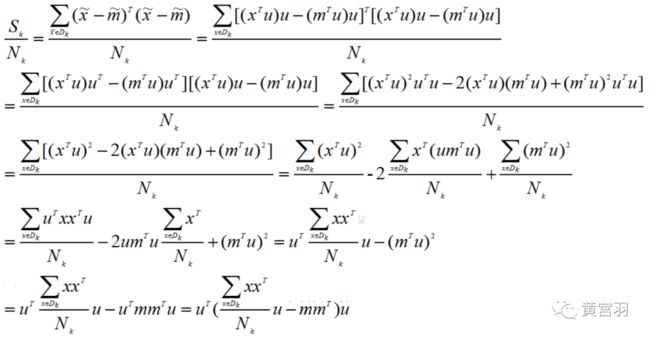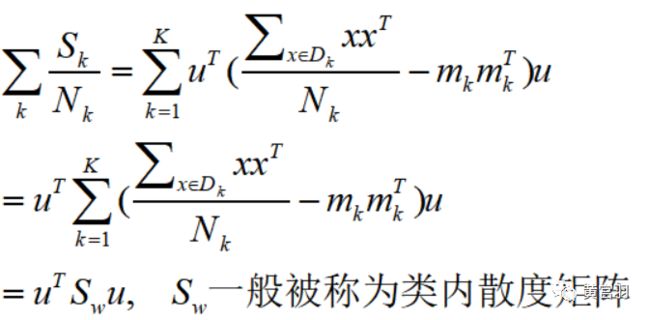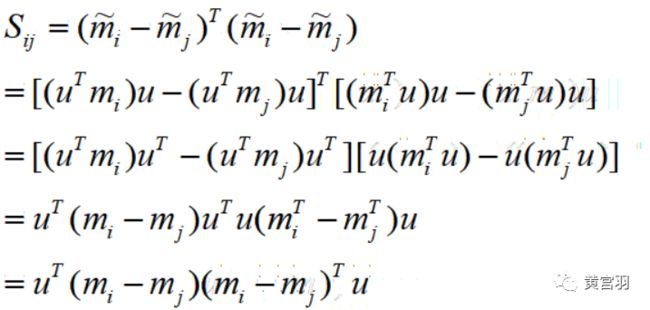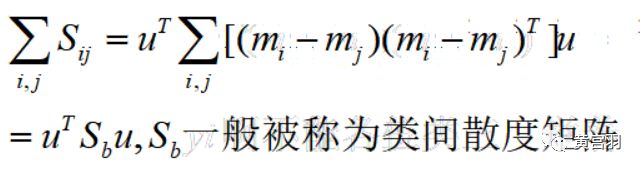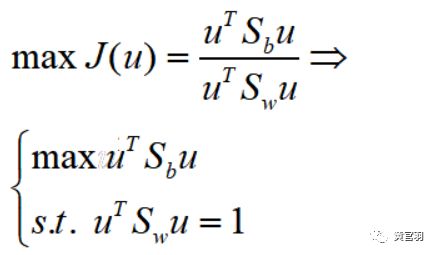特征工程之降维(LDA)
1.LDA是一种特征抽取的技术,用于分类任务的降维方法
2.其目标是向最大化类间差异,最小化类内差异的方向投影
3.LDA算法实现大致有六步:标准化数据集,均值化每个类别向量,计算类内散度矩阵和类间散度矩阵,构造S矩阵求解特征根与特征向量,组合W矩阵,计算降维数据集Z
LDA全称是Linear Discriminant Analysis。它属于一种特征抽取的技术,其目标是向最大化类间差异,最小化类内差异的方向投影,以利于将不同类的样本有效的分开,也就是用于分类任务的降维方法。
它跟PCA很相似,都是都是可用于降低数据集维度的线性转换技巧。它们的异同点如下:
| 降维方法 |
算法模式 |
目标 |
| PCA |
无监督式 |
寻找到方差最大的正交主成分分量轴 |
| LDA |
有监督式 |
最优化分类的特征子空间 |
下面从LDA需要用到的预备知识、算法推导、计算机实现做介绍。
1.预备知识
知识点1:共轭转置矩阵与Hermitan矩阵
共轭转置矩阵:先取共轭,再转置。
比如,对于矩阵A,其共轭为:
特别的,对于实矩阵,其共轭转置矩阵就是矩阵的转置
Hermitan矩阵:共轭转置矩阵和自己相等的矩阵
知识点2:瑞利商(Rayleigh quotient)
瑞利商指这样的函数:
特别的,当向量x是标准正交基时,瑞利商退化为:
该函数有性质,它的最大值等于矩阵 A 最大的特征值,而最小值等于矩阵 A 的最小的特征值:
知识点3:广义瑞利商(genralized Rayleigh quotient)
广义的瑞利商是指这样的函数:
通过将其通过标准化就可以转化为瑞利商的格式:
2.LDA算法推导
step1:假设样本共有K类,每一类的样本个数为N1,N2,...,Nk
step2:设变化后的每个样本为
step3:计算样本均值向量
step4:计算每类样本方差
step5:所有类别的样本方差之和
step6:计算不同类别i,j之间的中心距离
因此所有类别之间的距离之和为:
在已知条件下,求出类内散度矩阵和类间散度矩阵,接下来最大化类间距离,最小化类内方差
step7:利用拉格朗日乘数法求解最优解
step8:
计算矩阵S的最大的d个特征值和对应的特征向量W=(w1,w2,...,wd),即可得到投影矩阵,最后计算降维后的数据集Z = X*(W^T)
上面就是LDA降维算法的推导过程,这里需要注意两点
(1)选取特征值时,如果一些特征值明显大于其他的特征值,则取这些取值较大的特征值,因为它们包含更多的数据分布的信息。相反,如果一些特征值接近于0,我们将这些特征值舍去
(2)由于 W 是一个利用了样本类别得到的投影矩阵,因此它能够降维到的维度d的最大值为 K-1
3.算法实现
基于上一节推导结果,我们得到LDA算法实现流程:
1、对d维数据集进行标准化处理(d为特征数量)
2、对每一类别,计算d维的均值向量
3、构造类间的散度矩阵以及类内的散度矩阵
4、计算矩阵S(S具体定义见推导过程)的特征值所对应的特征向量
5、选取前k个特征值对应的特征向量,构造一个d x k维的转换矩阵W,特征向量以列的形式排列
6、使用转换矩阵W将样本映射到新的特征子空间上
小编用手动编写和调用sklearn内置包实现LDA算法。
首先,我们需要一个生成一个数据集:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets.samples_generator import make_classification
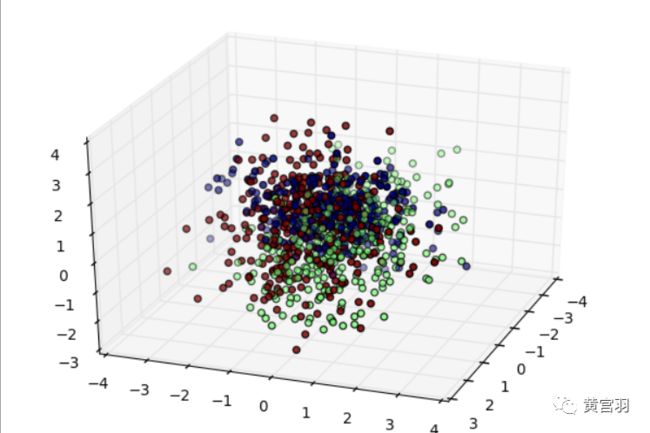
#生成3类3维特征的数据集
X, y = make_classification(n_samples=1000, n_features=3, n_redundant=0, n_classes=3, n_informative=2,
n_clusters_per_class=1,class_sep =0.5, random_state =10)
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o',c=y)
plt.show()数据集长这个样子,一共3类:
手动实现LDA
第一步,标准化数据集
Xmean = X.mean(axis=0)
Xstd = X- Xmean第二步,计算每个类别的向量均值
mean_vec = []
for k in np.unique(y):
mean_vec.append(np.mean(Xstd[y == k],axis=0)) #每一个特征维度的均值,这里规模是3*1第三步,计算类内散度矩阵和类间散度矩阵
d = 3
Sw = np.zeros((d,d)) #类内散度矩阵,规模是d*d(特征维度)
for k in np.unique(y):
#numpy对于一维向量,矩阵相乘需要用reshape得到d*d维矩阵,否则是一个数字
s = (Xstd[y == k].T).dot(Xstd[y == k])/(y[y==k].shape[0]) - (mean_vec[k].reshape(d,1)).dot(mean_vec[k].reshape(d,1).T)
Sw = Sw + s
Sb = np.zeros((d,d)) #类间散度矩阵,规模是d*d(特征维度)
for k in range(len(mean_vec)):
for j in range(k+1,len(mean_vec)):
sm = np.array(mean_vec[k] - mean_vec[j]).reshape(d,1)
Sb = Sb + np.dot(sm,sm.T)第四步,构造S矩阵(Sw逆矩阵乘以Sb矩阵),并求解特征向量和特征根
S = np.dot(np.linalg.inv(Sw),Sb)
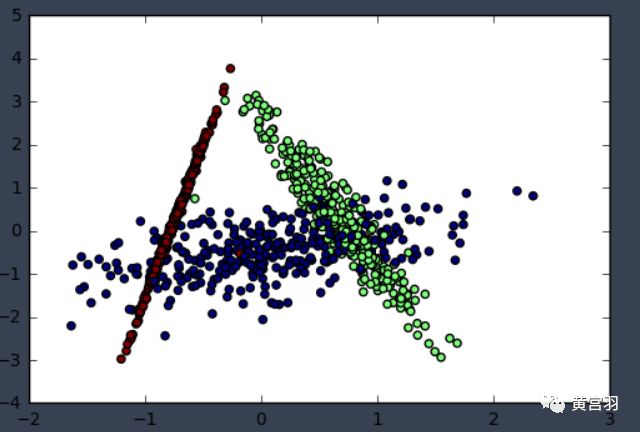
e,v = np.linalg.eig(S) #一列为一个特征向量第五步,组合W矩阵并计算降维后数据集Z
W = np.column_stack((v[:,0],v[:,1])) #向量组合用np.column_stack
Z = -np.dot(Xstd,W) #得到降维后的数据集最后,来看看降维效果
plt.scatter(Z[:, 0], Z[:, 1],marker='o',c=y)
plt.show()sklearn包实现LDA
直接调用sklearn包看看,结果和手动实现是否一致。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(Xstd,y)
X_new = lda.transform(Xstd)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=y)
plt.show()来看看结果
可见,结果是一致的。