清华计算几何大作业（六）:CG2017 PA4-1 Planar Range Query （平面区域查询）

1. 前置知识

计算几何算法：Kd-tree, Range Tree 或 Fractional Cascading ( Layered Range Tree )

推荐Range Tree，因为后面PA4-2要用。算法详见教材 5.2 kd-树(5.2 Kd-Trees)， 5.3 区域树(5.3 Range Trees)，5.6 *分散层叠 (5.6 *Fractional Cascading)

这里给到必要观看的视频课程章节，这些内容对理解和实现 平面区域查询 算法至关重要，标记有绿色√为必看章节（仅包含Range Tree，有兴趣的童鞋可以自己观看其他空间查找树的章节）：

2. 思路分析

问题描述：CG2017 PA4-1 Planar Range Query （平面区域查询）

2.1 Kd-Tree

虽然Kd-Tree的时间复杂度和实现难度要难于后面的Range Tree（不考虑Fractional Cascading），且时间复杂度也不如它，但它如何对空间进行划分思路，是值得我们学习的。所以这里我先介绍一下Kd-Tree相关的内容，如果有童鞋时间有限，想要快速完成这个作业，那推荐实现Range Tree，并且后面PA4-2的作业也需要用到它。

Kd-Tree的概念不难理解，大家可以结合视频课程上面的内容来理解，这里我们把精力放在下面两点上面：

• Degenerate Case（退化情况）；
• Kd-Tree的查询，即某个节点所界定的空间区域；

2.1.1 Degenerate Case

对于二位Kd-Tree，一共有两种退化情况：1）数个点在同一条垂直线上（相同x轴坐标），或2）数个点在同一条水平线上（相同y轴坐标），对于这些点的处理方法和我们在Point Location中的处理方法类似：

假象倾斜位于同一垂直（或水平）线上的点

具体的思路大家可以参考之前关于 Point Location 退化情况处理的文章（点定位（四）：处理退化情况(Point Location: handle degenerate cases)），这里就不再赘述。之前我们只考虑1）的情况，对于2）我们处理的方法类似，这里通过一个比较特殊的退化案例来说明具体的处理思路：

2.1.2 节点所界定的区域判定

Kd-Tree查询里面一个非常重要的概念就是某个节点所界定的范围区域，利用这个区域，我们才能判断是否需要进一步查询这个区域里面的数据点。关于这点教材介绍了相关的方法，就是查看某个节点的父节点，然后计算出该节点相应的界定区域¹：

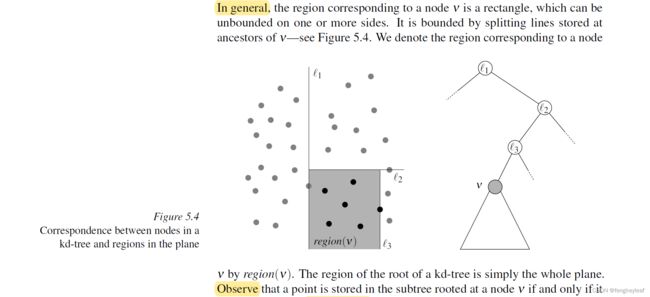
但具体到代码实现上，情况要相对复杂很多，根据笔者自己的观察，总结出下面几条规律：

对于任意节点Pi：

1）最多有三个父节点参与到界定该节点所界定的区域；

2）当参与界定的父节点有三个时，如果处于第二层的父节点与Pi都属于同侧子树，则最上层的父节点则不参与界定Pi所处的范围空间区域；

※ 注意1）中是最多三个父节点，也就是会出现只有两个，一个，甚至零个父节点的情况，比如当Kd-Tree中只有一个节点，则没有父节点，并且这个节点表示整个区域。

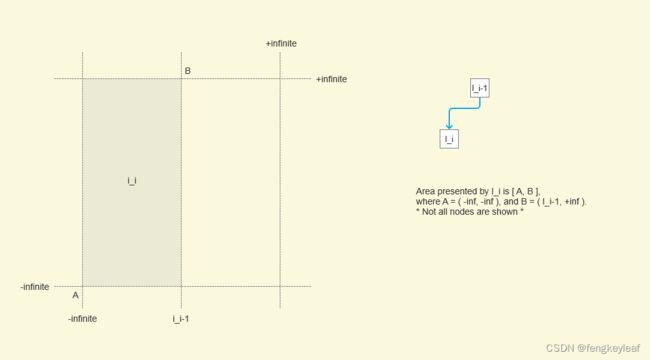
但这样会出现界定区域某一个方向是无限延伸的，这样的情况我们应该如何进行处理呢？答案也很简单，我们按“字面量”来处理，如果是无限延伸，就把这个方向的看成无限点。我们以只有一个父节点，且Pi表示垂直分割线为例：

大家可以看到节点l_i所界定的区域是由A和B两点所构成的正交矩形的部分（灰色区域），该区域的左，下和上边界都是无穷远的，所以我们用相应的无穷量来表示它们。对于这个思路，我们可以使用下面笔者总结的伪代码算法来描述：

算法 FINDBOUNDINGAREA(li)
输入：Kd-Tree某个节点li
输出：该节点li所界定的范围区域R[ A(x1, y1), B(x2, y2) ]，其中A为正交矩形的右下顶点，B为正交矩形的坐上顶点
(* -INF表示负无穷，+INF表示正无穷 * )
1. R <- [ A(-INF, -INF), B(+INF, +INF) ]
2. (* 假设l_i-1, l_i-2, l_i-3分别li的三级父节点，且l_i-3为最上层父节点 *)
3. if li 是奇数节点(* 表示此节点表示水平分割线 *)
    4. (* l_i-1, l_i-2, l_i-3 存在则分别执行相应赋值代码，不存在则保持不变 *)
	5. then if li 是 l_i-1 的左孩子
        6. then x2 <- l_i-1的x坐标值
        7. else x1 <- l_i-1的x坐标值
	8. if l_i-1 是 l_i-2 的左孩子
        9. then y2 <- l_i-2的y坐标值
        10. else y1 <- l_i-2的y坐标值
	11. then if l_i-2 不和 li 处于同一侧子树
        12. then if l_i-2 是 l_i-3 的左孩子
	        13. then x2 <- l_i-3的x坐标值
    	    14. else x1 <- l_i-3的x坐标值
    15. else (* li 是偶数节点, 表示此节点表示垂直分割线 *)
	    5. then if li 是 l_i-1 的左孩子
    	    6. then y2 <- l_i-1的y坐标值
        	7. else y1 <- l_i-1的y坐标值
		8. if l_i-1 是 l_i-2 的左孩子
    	    9. then x1 <- l_i-2的x坐标值
   	        10. else x2 <- l_i-2的x坐标值
		11. then if l_i-2 不和 li 处于同一侧子树
    	    12. then if l_i-2 是 l_i-3 的左孩子
	    	    13. then y2 <- l_i-3的y坐标值
    	    	14. else y1 <- l_i-3的y坐标值    
return R

通过这个方法，我们就能计算出某个节点所节点的空间区域，同样这个方法不仅能计算中间节点（Internal Node）的区域，也能用于计算叶节点（Leaf Node）的区域，但是否需要计算叶节点的区域，需要大家根据自己的实现思路来安排，这里仅提供计算思路。

2.2 Range Tree

相比起Kd-Tree，Range Tree的理解相对更加简单，实现起来也比较简单。大家可以把Range Tree看成多层结构树，每层分别对相应的坐标进行二分查找，所以它并不难。但是这里重点介绍一下教材上面关于Range Tree的高效实现细节²：

根据以上的描述，算法 BUILD2DRANGETREE 的运行时间并没有达到最优的 O(nlogn)。为了证明能够达到这一最优效率，在具体实现时必须有所讲究。如果根据 n 个未经排序的关键码来构造一棵二分查找树，的确需要消耗 O(nlogn)时间。这意味着在第 1 行构造联合结构时，就需要消耗 O(nlogn)时间。然而，由于 Py中的各点已经预先经过了排序，所以可以完成得更快⎯⎯只要按照自底向上的次序来构造二分查找树，总体的构造时间就将是线性的。因此，在构造的过程中，我们将维护对应于整个点集的两个列表：一个按照 x-坐标排序，另一个按照 y-坐标排序。按照这一方法，对于主树T 中的每一个节点，消耗的时间将线性正比于其对应正则子集的规模。这就意味着：总体的时间将与占用空间的规模相同，即 O(nlogn)。鉴于预排序所需的时间也不过是 O(nlogn)，故整个构造算法所需的时间还是 O(nlogn)。

这里的主要意思就是当我们构造Associated Structure（联合结构）时，如果每次都是先排序再去构造，会使每层的时间上限达到O(nlogn)，消耗太高，因为外层还需要进行O(logn)高度的构造，这样总的时间将会变成：O( n(logn) ^2)，并不是最佳的O(nlogn)。解决方法我们需要把每层Associated Structure的时间降为O(n)，这样总的时间就会变成最优。

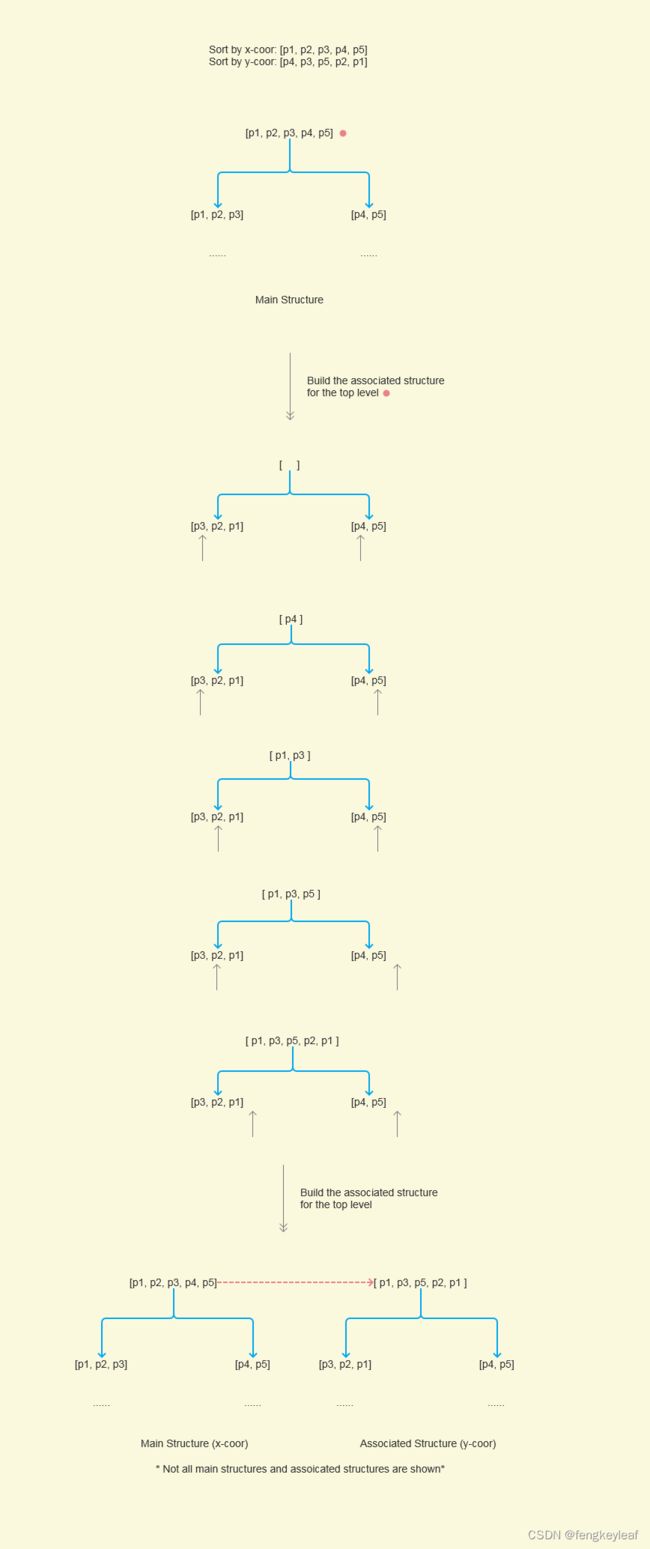
讲解到这里，这个过程不知道大家是否觉得非常熟悉呢？O(logn)的高度消耗，每层消耗O(n)，总的时间复杂度为O(nlogn)，怎么总感觉似曾相识的感觉呢？没错，有一个基础的排序就是利用上述的过程：Merge Sort（归并排序）。所以我们利用Merge Sort里面的归并过程来构造Associated Structure，具体的思路笔者用下面图例来描述：

2.3 Fractional Cascading ( Layered Range Tree )

对于Fractional Cascading，教材上面已经有详尽的说明和图例，所以这里就不再赘述。这里需要提醒一下在搜索结合Fractional Cascading的Range Tree结构的时候（此时的Associated Structure为Fractional Cascading，不再是之前的次一层的Range Tree），需要注意何时已经没有符合查询范围的数据点，也就是节点左或右节点指向Associated Structure为null，即当前位置不再有符合条件的点，所以需要结束查询。

最后这里给到三种空间范围查找树的时间空间复杂度对比表格，大家可以比对一下它们之间的优缺点：

数据结构	构造时间复杂度	查询时间复杂度	空间复杂度
Kd-Tree	O(nlogn)	O(√n+k)	O(n)
Range Tree	O(nlogn)	O(logn * logn + k)	O(nlogn)
Fractional Cascading	O(nlogn)	O(nlogn + k)	O(nlogn)

※ 上面数据结构的复杂度都是在2D情形下成立。

※ n指空间点集的个数，k指查询需要报告的点数。

3. 伪代码

这里只给到Range Tree相关的伪代码，Kd-tree的伪代码请参考教材，并且Fractional Casading教材没有伪代码，可以参考笔者的代码实现。

// 构造 2D Range Tree
Algorithm BUILD2DRANGETREE(P)
算法 BUILD2DRANGETREE (P)
Input. A set P of points in the plane.
Input: 平面点集 P
Output. The root of a 2-dimensional range tree.
Output: 一棵二维区域树的树根
1. Construct the associated structure: Build a binary search tree Tassoc on the set Py of y-coordinates of the points in P. Store at the leaves of Tassoc not just the y-coordinate of the points in Py, but the points themselves.
1. 构造联合结构：令 Py为由 P 中各点的 y-坐标组成的集合，构造一棵存储 Py的二分查找树 Tassoc, Tassoc的各匹叶子，不仅要存储 Py中的 y-坐标，还要存储该坐标所对应的点
2. if P contains only one point
2. if (P 只包含一个点)
	3. then Create a leaf ν storing this point, and make Tassoc the associated structure of ν.
	3. then 生成一匹叶子来存储这个点，并将 Tassoc当作与 v 对应的联合结构
	4. else Split P into two subsets; one subset Pleft contains the points with x-coordinate less than or equal to xmid, the median x-coordinate, and the other subset Pright contains the points with x-coordinate larger than xmid.
	4. else (* 设 xmid为 P 中各点 x-坐标的中值 *) 将 P 划分为两个子集 Pleft和 Pright, eft 由所有 x-坐标小于或者等于 xmid的点组成, right由所有 x-坐标大于 xmid 的点组成
		5. νleft <- BUILD2DRANGETREE(Pleft)
		5. νleft <- BUILD2DRANGETREE(Pleft)
		6. νright <- BUILD2DRANGETREE(Pright)
		6. νright <- BUILD2DRANGETREE(Pright)
		7. Create a node ν storing xmid, make νleft the left child of ν, make νright the right child of ν, and make Tassoc the associated structure of ν.
		7. 生成一个节点 v 以存储 xmid, 将 vleft 做为 v 的左孩子, 将 vright做为 v 的右孩子, 将 Tassoc做为 v 的联合结构
8. return ν
8. return ν

// 查询 2D Range Tree
Algorithm 2DRANGEQUERY(T,[x : x']×[y : y'])
算法 2DRANGEQUERY (T, [x : x'] × [y : y'])
Input. A 2-dimensional range tree T and a range [x : x']×[y : y'].
输入：二维区域树 T，以及待查询区域[x : x'] × [y : y']
Output. All points in T that lie in the range.
输出：T 中位于[x : x'] × [y : y']之内的所有点
1. νsplit ←FINDSPLITNODE(T,x,x')
1. νsplit ←FINDSPLITNODE(T,x,x')
2. if νsplit is a leaf
2. if (vsplit是叶子)
	3. then Check if the point stored at νsplit must be reported.
	3. then 检查 vsplit处所存储的点是否应该被报告出来
	4. else (* Follow the path to x and call 1DRANGEQUERY on the subtrees right of the path. *)
	4. else (* 沿着通往 x 的路径，对路径右侧的每棵子树调用一次 1DRANGEQUERY *)
		5. ν ← lc(νsplit)
		5. ν ← lc(νsplit)
		6. while ν is not a leaf
		6. while (v 还不是叶子)
			7. do if x <= xν
			7. do if x <= xν
				8. then 1DRANGEQUERY(Tassoc(rc(ν)),[y : y'])
				8. then 1DRANGEQUERY(Tassoc(rc(ν)),[y : y'])
				9. ν ← lc(ν)
				9. ν ← lc(ν)
			10. else ν ← rc(ν)
			10. else ν ← rc(ν)
		11. Check if the point stored at ν must be reported.
		11. 检查 v 处所存储的点是否应该被报告出来
12. Similarly, follow the path from rc(νsplit) to x', call 1DRANGEQUERY with the range [y : y'] on the associated structures of subtrees left of the path, and check if the point stored at the leaf where the path ends must be reported.
12. (* 类似地 *) 沿着从 rc(vsplit)通往 x'的路径，对路径左侧的每棵子树所对应的联合结构, 针对区域[y : y']调用一次 1DRANGEQUERY；检查路径终点处的那匹叶子，看看是否应该将存储于其中的点报告出来

// 查询 2D Range Tree 所需要使用的 1D 查询算法
// 查找分叉节点
FINDSPLITNODE(T,x,x')
算法 FINDSPLITNODE(T, x, x')
Input. A tree T and two values x and x' with x <= x'.
输入：树 T，以及两个数值 x 和 x'，x ≤ x'
Output. The node ν where the paths to x and x' split, or the leaf where both paths end.
输出：从树根出发、分别通往 x 和 x'的两条路径的分叉点 v (* 若这两条路径完全重合，则返回它们共同的终点 *)
1. ν ← root(T)
1. v ← root(T)
2. while ν is not a leaf and (x' <= xν or x > xν )
2. while (v 还不是叶子) 且 (x' ≤ xv 或 x > xv)
	3. do if x' <= xν
	3. do if (x' ≤ xv)
		4. then ν <- lc(ν)
		4. then ν <- lc(ν)
		5. else ν <- rc(ν)
		5. else ν <- rc(ν)
6. return ν
6. return ν

// 1D Range Query
Algorithm 1DRANGEQUERY(T,[x : x'])
算法 1DRANGEQUERY (T, [x : x'])
Input. A binary search tree T and a range [x : x'].
输入：二分查找树 T，待查询区域[x : x']
Output. All points stored in T that lie in the range.
输出：存储于 T 中、落在[x : x']内的所有点
1. νsplit <- FINDSPLITNODE(T,x,x')
1. νsplit <- FINDSPLITNODE(T,x,x')
2. if νsplit is a leaf
2. if (vsplit是叶子)
	3. then Check if the point stored at νsplit must be reported.
	3. then 检查 vsplit对应的点是否应该被报告
	4. else (* Follow the path to x and report the points in subtrees right of the path. *)
	4. else (* 沿着通往 x 的路径，报告路径右侧每一子树内的所有点 *)
		5. ν <- lc(νsplit)
		5. ν <- lc(νsplit)
		6. while ν is not a leaf
		while (v 还不是叶子)
			7. do if x <= xν
			do if (x ≤ xv)
				8. then REPORTSUBTREE(rc(ν))
				8. then REPORTSUBTREE(rc(ν))
					9. ν <- lc(ν)
					9. ν <- lc(ν)
				10. else ν <- rc(ν)
				10. else ν <- rc(ν)
		11. Check if the point stored at the leaf ν must be reported.
		11. 检查叶子 v 对应的点是否应该被报告
12. Similarly, follow the path to x', report the points in subtrees left of the path, and check if the point stored at the leaf where the path ends must be reported.
12. 类似地，沿着通往 x'的路径，报告路径左侧每一子树内的所有点检查该路径终点（叶子）对应的点是否应该被报告

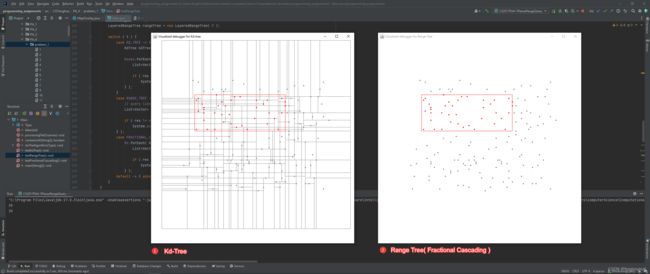
4. 可视化结果示例

这里给到三种空间范围查找树的可视化结果示例，因为Range Tree和Fractional Cascading在可视化上面没有区别，所以两者共用一个可视化结果：

5. 项目代码（待更新完整）

个人作业项目代码：Algorithm

6. 拓展（Follow-ups）

• 实现其他空间范围查找树结构：Kd-Tree, Factional Cascading
• 让Range Tree（包括Fractional Cascading）有查找无穷范围( [-INF, -INF]x[+INf, +INF] )的能力，即报告出所有数据点（后面正交矩形窗口查询算法需要使用） - 笔者代码已实现

---

上一节：CG2017 PA3-2 Which wall are you looking at （你在看哪面墙）

下一节：CG2017 PA4-2 Orthogonal Windowing Query （正交矩形窗口查询）

系列汇总：清华计算几何大作业思路分析和代码实现

7. 参考资料

1. Computational Geometry: Algorithms and Applications
2. 计算几何 ⎯⎯ 算法与应用, 邓俊辉译，清华大学出版社
3. 计算几何 | Computational Geometry

8. 免责声明

※ 本文之中如有错误和不准确的地方，欢迎大家指正哒~
※ 此项目仅用于学习交流，请不要用于任何形式的商用用途，谢谢呢；

---

---

1. Computational Geometry: Algorithms and Applications ↩︎

2. 计算几何 ⎯⎯ 算法与应用, 邓俊辉译，清华大学出版社 ↩︎