李沐动手学深度学习V2-转置卷积和代码实现

一.转置卷积

1. 介绍

卷积神经网络层中卷积层和汇聚层，通常会减少下采样输入图像的空间维度（高和宽）。 然而如果输入和输出图像的空间维度保持相同，在以像素级分类的语义分割中将会很方便，输出像素所处的通道维可以保存有输入像素在同一位置上的分类结果。
为了实现这一点，尤其是在空间维度被卷积神经网络层缩小后，可以使用另一种类型的卷积神经网络层，它可以增加上采样中间层特征图的空间维度。下面介绍转置卷积（transposed convolution）， 用于逆转下采样导致的空间尺寸减小。

2. 转置卷积计算

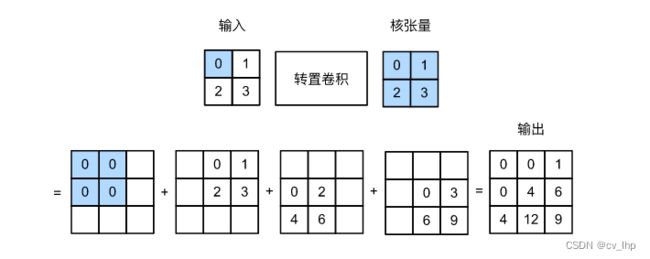
先暂时忽略通道（通道为1），从基本的转置卷积开始，设步幅为1且没有填充。假设有一个$n_h\times n_w$的输入张量和一个$k_h\times k_w$的卷积核，以步幅为1滑动卷积核窗口，每行$n_w$次，每列$n_h$次，共产生$n_h{n}_w$个中间结果。每个中间结果都是一个$(n_h+k_h-1)\times (n_w+k_w-1)$的张量，初始化为0。为了计算每个中间张量，输入张量中的每个元素都要乘以卷积核，从而使所得的$k_h\times k_w$张量替换中间张量的一部分。注意每个中间张量被替换部分的位置与输入张量中元素的位置相对应。最后，所有中间结果相加以获得最终结果。
如下图所示解释了如何为$2\times 2$的输入张量计算卷积核为$2\times 2$的转置卷积。

3.实现基本转置卷积计算

对输入矩阵X和卷积核矩阵K实现基本的转置卷积运算，与通过卷积核“减少”输入元素的常规卷积相比，转置卷积通过卷积核“广播”输入元素，从而产生大于输入的输出。

import torch
import d2l.torch
from torch import nn
#此实现是基本的二维转置卷积运算。
def transposed_conv(X,K):
    h,w = K.shape[0],K.shape[1]
    Y = torch.zeros(size=(X.shape[0]+h-1,X.shape[1]+w-1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i:i+h,j:j+w] += X[i,j]*K
    return Y
X = torch.tensor([[0.0,1.0],[2.0,3.0]])
K = torch.tensor([[0.0,1.0],[2.0,3.0]])
#构建输入张量X和卷积核张量K验证上图实现输出
transposed_conv(X,K)

当输入X和卷积核K都是四维张量时，可以使用高级API获得相同的结果。

X = X.reshape(1,1,2,2)
K = K.reshape(1,1,2,2)
conv_transpose2d = nn.ConvTranspose2d(in_channels=1,out_channels=1,kernel_size=2,bias=False)
conv_transpose2d.weight.data = K
Y = conv_transpose2d(X)
Y

4. 填充、步幅和多通道

1. 与常规卷积不同，在转置卷积中，填充被应用于的输出（常规卷积将填充应用于输入）。 例如当将高和宽两侧的填充数指定为1时，转置卷积的输出中将删除第一和最后的行与列。

conv_transpose = nn.ConvTranspose2d(1,1,kernel_size=2,padding=1,bias=False)
conv_transpose.weight.data = K
conv_transpose(X)

2. 在转置卷积中步幅用于转置卷积结果移动的步数，而不是作用于输入，如下图所示。
   

#步幅为2的转置卷积的输出
conv_transpose = nn.ConvTranspose2d(1,1,kernel_size=2,stride=2,bias=False)
conv_transpose.weight.data = K
conv_transpose(X)

3. 对于多个输入和输出通道，转置卷积与常规卷积以相同方式运作。假设输入有$c_i$个通道，且转置卷积为每个输入通道分配了一个$k_h\times k_w$的卷积核张量。当指定多个输出通道时，每个输出通道将有一个$c_i\times k_h\times k_w$的卷积核。
   同样，如果将$\mathsf{X}$代入卷积层$f$来输出$\mathsf{Y}=f(\mathsf{X})$，并创建一个与$f$具有相同的超参数、但输出通道数量是$\mathsf{X}$中通道数的转置卷积层$g$，那么$g(Y)$的形状将与$\mathsf{X}$相同，如下面示例代码。

X = torch.rand((1,10,16,16))
conv2d = nn.Conv2d(in_channels=10,out_channels=20,kernel_size=5,padding=2,stride=3)
tconv2d = nn.ConvTranspose2d(in_channels=20,out_channels=10,kernel_size=5,padding=2,stride=3)
tconv2d(conv2d(X)).shape == X.shape

5. 与矩阵变换的联系

下面代码定义了一个 3×3 的输入X和 2×2 卷积核K，然后使用corr2d（）函数计算卷积输出Y。

X = torch.arange(9.0).reshape(3,3)
K = torch.tensor([[1.0,2.0],[3.0,4.0]])
Y = d2l.torch.corr2d(X,K)
Y

将卷积核K重写为包含大量0的稀疏权重矩阵W，权重矩阵的形状是(4,9)，其中非0元素来自卷积核K。

def kernel2matrix(K):
    k,W = torch.zeros(5),torch.zeros((4,9))
    k[0:2],k[3:5] = K[0,:],K[1,:]
    W[0,:5],W[1,1:6],W[2,3:8],W[3,4:] = k,k,k,k
    return W
W = kernel2matrix(K)
W

将输入X变为一维向量，再与权重矩阵W进行矩阵乘法，与上面使用corr2d（）函数实现卷积的结果相同

Y == torch.matmul(W,X.reshape(-1)).reshape(2,2)
'''
输出结果：
tensor([[True, True],
        [True, True]])
'''

同样可以使用矩阵乘法来实现转置卷积，如下面代码中将上面的常规卷积 2×2 的输出Y作为转置卷积的输入，想要通过矩阵相乘来实现它，只需要将权重矩阵W的形状转置为 (9,4) 。

Z = transposed_conv(Y,K)
Z == torch.matmul(W.T,Y.reshape(-1)).reshape(3,3)
'''
输出结果如下：
tensor([[True, True, True],
        [True, True, True],
        [True, True, True]])
'''

抽象来看，给定输入向量$\mathbf{x}$和权重矩阵$\mathbf{W}$，卷积的前向传播函数可以通过将其输入与权重矩阵相乘并输出向量$\mathbf{y}=\mathbf{W}\mathbf{x}$来实现。
由于反向传播遵循链式法则和${\nabla }_{\mathbf{x}}\mathbf{y}={\mathbf{W}}^{\top }$，卷积的反向传播函数可以通过将其输入与转置的权重矩阵${\mathbf{W}}^{\top }$相乘来实现。
因此，转置卷积层能够交换卷积层的正向传播函数和反向传播函数：它的正向传播和反向传播函数将输入向量分别与${\mathbf{W}}^{\top }$和$\mathbf{W}$相乘。

6.小结

• 与通过卷积核减少输入元素的常规卷积相反，转置卷积通过卷积核广播输入元素，从而产生形状大于输入的输出。
• 如果我们将$\mathsf{X}$输入卷积层$f$来获得输出$\mathsf{Y}=f(\mathsf{X})$并创造一个与$f$有相同的超参数、但输出通道数是$\mathsf{X}$中通道数的转置卷积层$g$，那么$g(Y)$的形状将与$\mathsf{X}$相同。
• 可以使用矩阵乘法来实现卷积和转置卷积，转置卷积层能够交换卷积层的正向传播函数和反向传播函数。
• 转置卷积也是一种卷积
• 注意转置卷积的卷积核的权重形状（基于Pytorch中nn.ConvTranspose2d()函数）为：(in_channels,out_channels,height,width)，而卷积的卷积核的权重形状为：(out_channels,in_channels,height,width)，两者权重形状大小不要弄混了。

7.全部代码

import torch
import d2l.torch
from torch import nn

def transposed_conv(X, K):
    h, w = K.shape[0], K.shape[1]
    Y = torch.zeros(size=(X.shape[0] + h - 1, X.shape[1] + w - 1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i:i + h, j:j + w] += X[i, j] * K
    return Y

X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
transposed_conv(X, K)
X = X.reshape(1, 1, 2, 2)
K = K.reshape(1, 1, 2, 2)
conv_transpose2d = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=2, bias=False)
conv_transpose2d.weight.data = K
Y = conv_transpose2d(X)
Y
conv_transpose = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
conv_transpose.weight.data = K
conv_transpose(X)
conv_transpose = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
conv_transpose.weight.data = K
conv_transpose(X)
X = torch.rand((1, 10, 16, 16))
conv2d = nn.Conv2d(in_channels=10, out_channels=20, kernel_size=5, padding=2, stride=3)
tconv2d = nn.ConvTranspose2d(in_channels=20, out_channels=10, kernel_size=5, padding=2, stride=3)
tconv2d(conv2d(X)).shape == X.shape
X = torch.arange(9.0).reshape(3, 3)
K = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
Y = d2l.torch.corr2d(X, K)
Y


def kernel2matrix(K):
    k, W = torch.zeros(5), torch.zeros((4, 9))
    k[0:2], k[3:5] = K[0, :], K[1, :]
    W[0, :5], W[1, 1:6], W[2, 3:8], W[3, 4:] = k, k, k, k
    return W


W = kernel2matrix(K)
W
Y == torch.matmul(W, X.reshape(-1)).reshape(2, 2)
Z = transposed_conv(Y, K)
Z == torch.matmul(W.T, Y.reshape(-1)).reshape(3, 3)

二. 李沐老师对转置卷积的第二种讲法

下面是李沐老师对转置卷积的第二种讲法的截图

注意下图第三步表示：对变化后的输入和卷积核始终使用填充为0，步幅为1的卷积核进行计算得到输出，填充和步幅不是使用转置矩阵的填充和步幅。

注意下图第三步表示：对变化后的输入和卷积核始终使用填充为0，步幅为1的卷积核进行计算得到输出，填充和步幅不是使用转置矩阵的填充和步幅。

注意下图第三步表示：对变化后的输入和卷积核始终使用填充为0，步幅为1的卷积核进行计算得到输出，填充和步幅不是使用转置矩阵的填充和步幅。

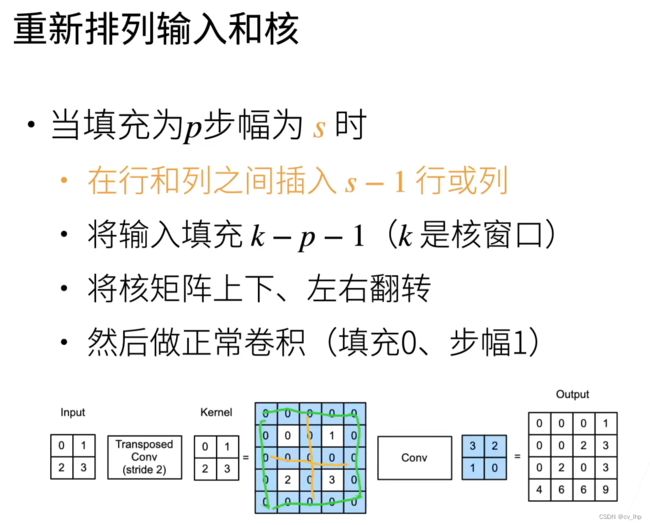
转置卷积是一种变化了输入和卷积核的卷积，来得到上采样的目的。变化了的输入是指上图2，3，4中对输入进行变换，变化了的卷积核是指将该卷积核上下左右进行翻转。

三. 卷积和转置卷积输出尺寸的计算公式如下图所示