基于算法概念的可解释推理AAAI2022(用于组合优化问题)
目录
- 摘要
- 1.Introduction
- 2.Related Work
-
- 2.1.GNN Explainability
- 2.2.基于概念的解释
- 2.3.Combinatorial Optimisation for GNNs
- 3.Methodology
-
- Encode-process-decode
- Explicitly relational GNN architecture
- Extracting node-level algorithm rules
- Extracting node-level algorithm rules
- 实验
- 个人理解
- 附加内容:基于概念的解释
摘要
最近对图神经网络(GNN)模型的研究成功地将GNN应用于经典图算法(classical graph algorithms)和组合优化问题(combinatorial optimisation problems)。这有许多好处,例如允许在不满足前提条件时应用算法,或者在没有足够的训练数据或无法生成足够的训练数据时重用(reusing)学习模型。不幸的是,这些方法的一个主要障碍是缺乏可解释性,因为GNN是无法直接解释的黑盒模型。在这项工作中,我们通过将基于概念解释方面的现有工作应用于GNN模型来解决这一局限性。我们介绍了概念瓶颈GNN(CBGNN,concept-bottleneck GNNs),它依赖于对GNN读出机制的修改。通过三个案例研究,我们证明:
- 我们提出的模型能够准确地学习概念,并根据每个目标类的概念提取命题公式(propositional formulas);
- 我们基于概念的GNN模型实现了与最先进模型的比较性能;
- 我们可以导出全局图概念(global graph concepts),而无需对图级概念进行任何明确的监督。
1.Introduction
图形神经网络(GNNs)已成功应用于涉及不规则结构数据的问题,如量子化学、药物发现、社交网络和物理模拟。GNN研究的最新领域之一集中于使用GNN模拟经典算法(2021年兴起)。特别是,本研究探索了GNN在迭代算法、基于指针的数据结构,甚至规划任务中的应用。重要的是,这些工作表明GNN能够很强地推广到比训练期间看到的图大得多的输入图。
不幸的是,在上述所有情况下,这些最先进的GNN模型都是黑箱,其行为无法直接解释。在实践中,这可能导致对此类模型缺乏置信度,使得在医疗保健等安全关键应用中使用这些模型具有挑战性。此外,这种缺乏可解释性的情况也使得提取此类模型所学知识变得困难,这妨碍了用户更好地理解相应的任务。
最近关于可解释AI(XAI,Explainable AI)的研究引入了一种新型的卷积神经网络(CNN)解释方法,称为基于概念的可解释性(concept-based explainability)。基于概念的解释以人类可以理解的单位提供模型解释,而不是单独的特征或像素(例如,车轮和车门的概念对于检测汽车很重要)。尤其是,概念瓶颈模型(CBM)的研究依赖于概念,并引入了一种新型的可解释CNN,它分两个不同的步骤执行输入处理:从输入计算一组概念,然后从概念计算输出标签。
本文通过引入基于概念瓶颈的图神经网络,将CBMs的思想应用到GNN模型中。特别是,我们依赖encode-process-decode范式,并在GNN模型输出之前应用概念瓶颈层(见图1)。通过这样做,我们能够为步骤级组合优化方法的步骤更新提取"更新/终止规则"(update/termination rules)。
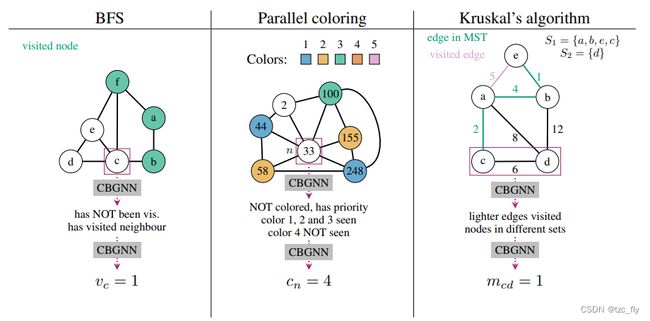
- 图1:我们的概念瓶颈图神经网络(CBGNN)方法概述。重要的是,可以训练CBGNN模型来提取给定任务的概念信息以及算法规则。我们给出了3种算法的示例,展示了CBGNN如何从输入数据中提取概念,然后使用这些概念计算输出。
重要的是,我们表明,通过依赖一组合适的概念并对其进行监督,我们能够推导出经典算法的规则,如广度优先搜索和Kruskal算法,以及更高级的启发式算法,如图着色(parallel graph coloring)。此外,我们还提出了一种利用节点级概念提取图级规则的方法。我们的评估实验表明,我们提取的所有规则都能很好地推广到5倍更大的图。
综上所述,我们在这项工作中做出了以下贡献:
- 提出了一种基于概念处理的概念瓶颈图神经网络(CBGNN)。据我们所知,这是首次将概念瓶颈方法应用于GNN。
- 使用三个不同的案例研究(BFS、图着色和Kruskal)对我们的方法进行定量评估,结果表明,我们的CBGNN方法能够实现与现有最先进技术相当的性能。
- 定性评估我们的方法,演示如何使用CBGNN模型的概念来总结CBGNN所学启发式的规则。
2.Related Work
2.1.GNN Explainability
GNN解释性最近的工作开始探索XAI技术在GNN环境中的应用。例如,将用于CNN的特征重要性和基于梯度(feature-importance gradient-based)的方法(如类激活映射Class Activation Mappings或分层相关性传播Layer-wise Relevance Propagation)改到GNN上,以找到负责预测的最重要节点或者子图。或者,Ying等人(2019年)的工作;Vu和Thai(2020年);Luo等人(2020年)专注于GNN解释性特有的更复杂方法,例如基于互信息最大化的方法,或特征解释的马尔可夫覆盖条件概率。重要的是,这些工作专注于GNN任务和涉及社交网络、化学或药物发现的benchmark,而不是专注于组合优化任务,这是本工作的重点。此外,这些工作侧重于以事后的方式解释预先训练的GNN,而我们侧重于构建基于设计的解释GNN模型。最后,这些工作侧重于基于特征重要性的解释方法(即识别输入节点/子图的重要性),而我们依赖基于概念的解释方法。
2.2.基于概念的解释
基于概念的可解释性一系列现有的研究已经探索了,各种应用于CNN模型的基于概念的解释。例如,Ghorbani等人(2019年)的工作;Kazhdan等人(2020年);Yeh等人(2019年)介绍了以无监督或半监督方式从预先训练的CNN中提取概念的方法。Chen等人(2020年)的工作;Koh等人(2020年)依靠概念引入设计解释的CNN模型,分两个不同的步骤进行处理:概念提取和标签预测。关于概念的其他工作包括研究概念与可分离学习(concepts and disentanglement learning)之间的联系,Kazhdan等人以及Wijaya等人将概念用于数据分布转移(data distribution shifts)。重要的是,这些工作仅在CNN背景下探索概念,Kazhdan等人是唯一在RNN模型背景下探索概念的工作。在这项工作中,我们关注GNNs基于概念的解释性,其中,与Koh 等人的工作类似,概念是人为指定(human-specified)的。
2.3.Combinatorial Optimisation for GNNs
GNN的组合优化遵循Cappart等人定义的层次结构,我们的工作分类为步骤级方法。我们直接扩展了Velickovic等人的工作,因此我们使用这些工作中提出的模型作为baseline。我们不会将我们的模型与算法级组合优化方法或单位级方法进行比较,原因如下:算法级方法通常为每个数据样本提供一个输出(而不是每个步骤一个输出),但给定算法的规则/不变性(invariants)来自于迭代的方式,使得算法级组合优化不太适合概念瓶颈。单元级学习侧重于学习基本的计算单元,例如获取最大值或合并列表,然后手动组合这些列表-在这一级进行解释不会有很大好处。据我们所知,只有Velickovic等人试图使用GNNexplaner解释GNN预测。然而,他们的模型无法通过设计进行解释,并且要对单个样本进行进一步优化,以给出局部解释。之前的所有其他工作都是以黑匣子的方式运作的,没有考虑所学模型的可解释性。
3.Methodology
Encode-process-decode
CBGNN通过encode-process-decode架构对图进行计算。对于每个算法 A A A,encoder network f A f_{A} fA将特定于算法的节点级输入 z i ( t ) z_{i}^{(t)} zi(t)编码到latent space。使用processor network P P P 处理这些节点embedding,通常是一个GNN。processor取 Z ( t ) = { z i ( t ) } i ∈ V Z^{(t)}=\left\{z_{i}^{(t)}\right\}_{i\in V} Z(t)={zi(t)}i∈V和edge index E E E生成latent features H ( t ) = { h i t ∈ R ∣ L ∣ } i ∈ V H^{(t)}=\left\{h_{i}^{t}\in R^{|L|}\right\}_{i\in V} H(t)={hit∈R∣L∣}i∈V,其中 ∣ L ∣ |L| ∣L∣是latent维数。对比以前的工作,我们首先通过decoder network g A ′ g_{A}' gA′传递latent embedding计算输出,deocoder生成每个节点的概念 C ( t ) = { c i ( t ) ∈ ( 0 , 1 ) ∣ C ∣ } C^{(t)}=\left\{c_{i}^{(t)}\in(0,1)^{|C|}\right\} C(t)={ci(t)∈(0,1)∣C∣},其中 ∣ C ∣ |C| ∣C∣是概念的数量。然后这些概念通过concept decoder g A g_{A} gA生成节点级输出 Y ( t ) = { y i ( t ) } Y^{(t)}=\left\{y_{i}^{(t)}\right\} Y(t)={yi(t)}。
在适用的情况下,我们还利用终止网络 termination network T A T_A TA来决定何时停止。然而,与之前的工作相比,我们观察到,如果我们基于潜在的下一步embedding计算终止概率(即,关于迭代执行后的状态的置信度),那么训练会更加稳定。此外,我们发现使用平均节点embedding作为 T A T_A TA的输入是不够的。相反,我们选择使用具有一个注意力头的自适应 PrediNet 架构的输出。PrediNet用于表示基本命题的连接,因此它可以(理论上)捕获终止规则的逻辑偏差。整个过程总结在图2以及以下方程式中:
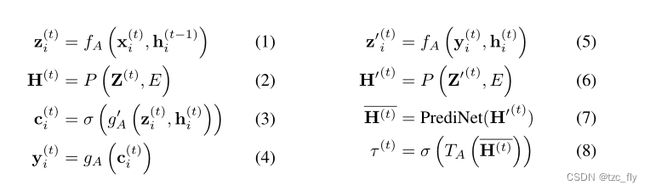
其中, σ \sigma σ是logistic sigmoid函数。当使用 T A T_{A} TA,如果 τ ( t ) > 0.5 \tau^{(t)}>0.5 τ(t)>0.5,公式(1)-(8)会重复。
- 图2:我们的GNN结构。左边:公式(1)-(4),为了生成节点级输出,消息从邻居节点 m i j m_{ij} mij结合当前节点表示 h b h_{b} hb,生成更新的节点表示 h b ′ h_{b}' hb′。然后从更新的表示中提取概念 c b c_b cb,并从概念中提取节点级输出 y b y_b yb。右边:公式(5)-(8), 通过将节点embedding通过PrediNet得到图级embedding( h G h_G hG)。我们直接从潜在状态 h G h_G hG中提取图级输出 y G y_G yG(在我们的例子中是终止概率),图级概念是通过节点概念上的完全枚举方法提取的。
编码输入与给定节点的潜在状态的组合不仅包含关于给定步骤的输出的足够信息,而且还包含:
- 1.节点的当前状态;
- 2.对其邻居中其他节点状态的观测;
如果我们的概念被设计为获取1和2的知识,然后,我们可以提取有意义的算法输出解释,而无需提供关于算法如何工作的任何明确信息(定理、不变量等)。
Explicitly relational GNN architecture
一些图级任务(例如决定算法是否终止)可以简化为图中所有节点的逻辑公式。本文中,上述消息传递的迭代的终止规则可以简化为具有特定属性的节点的存在。作者提出了一个终止网络 T A T_{A} TA,以节点embedding作为输入,利用改编的带有单个注意力头的PrediNet模型生成图级概念 h G h_{G} hG,从而输出迭代终止的概率,即图级输出 y G y_{G} yG。
Extracting node-level algorithm rules
由于CBGNN主要对GNN的读出阶段作修改,因此作者主要聚焦于decode阶段的实现。概念解码器 g A g_{A} gA的权重 W W W决定了算法的节点级输出公式(权重越大,代表其对应的概念越重要)。为实现上述输出目标,CBGNN使用了开源包logic_explained_networks,该包以解码器的权重、训练数据的预测概念和训练数据的真实标签作为输入,输出概念之间的析取范式作为逻辑解释。进一步地,为获得简明的逻辑解释规则,CBGNN在损失函数中添加一个正则化项,以删除占比较低的概念:
![]()
其中, Ⅱ Ⅱ Ⅱ是指示函数, W 1 W^{1} W1是第一层的权重。
Extracting node-level algorithm rules
为决定算法何时终止迭代,作者采用枚举的方法,在每次迭代中,提取图中的节点概念,当其均满足预定的终止规则时,即可停止算法迭代。
实验
本文选择三个典型的图算法作为案例研究,其对应的概念解释示例如下,即对于给定算法,输入图数据,在更新节点消息后,提取节点对应概念,利用概念组合而成的逻辑公式进行推理,从而输出预测结果:

- 表1:算法与对应的概念,以及ground truth的解释示例。
实验的训练数据使用人工构造(根据某个图算法定义生成对应的数据集)。
CBGNN是在推理过程中实现可解释的,可以针对算法和人为定义的概念(节点级概念),推广到相同算法处理的问题,并提取概念之间的逻辑关系。
实验证明CBGNN可以在保证模型性能的前提下准确学习节点级概念,并将其组合为析取范式以推断输出。进一步地,CBGNN还可以对某些图级任务执行无监督的规则提取(例如决定算法何时终止),提取的规则依然是可解释的,不会严重影响模型的准确性。
个人理解
这是GNN在组合优化问题下的可解释应用,合理的原因在于,在GNN推理过程中人工设计了概念处理这个层(瓶颈),从而增加了网络在学习组合优化问题数据集分布中的约束。
附加内容:基于概念的解释
目前我们熟知的可解释是在模型中间输出上做工作,观察特征的重要程度,找到某些特征图的含义等等。其实这些工作本质也是在找到可解释的概念。
2018年,谷歌将可解释性原则总结如下,这些总结或许对我们未来的工作有指导:
- 理解隐藏层做了什么:深度学习模型中的大部分知识是在隐藏层中形成的。要解释深度学习模型,必须要从宏观角度理解不同隐藏层的功能。
- 理解神经元节点是如何激活的:可解释性的关键不是理解网络中单一神经元的功能,而是要理解在同一空间位置一起激活的互相连接的神经元组。通过互相连接的神经元组分割网络可以从更简单的抽象层次来理解其功能。
- 理解概念是如何形成的:深度神经网络如何形成可组装成最终输出的一个个概念。
如前所述,可解释性的一般方法应该是根据深度模型所考虑的输入特征来描述其预测结果。一个经典例子就是 logistic 回归分类器,一般会把分类器中的系数权重解释为每个特征的重要性。但大部分深度学习模型在特征层面(如像素值)的运算,无法和人类能轻易理解的高级概念对应。此外,模型的内部值(例如神经元激活)是无法理解的。尽管像显著性图(saliency map)这样的技术可以有效测量特定像素区域的重要性,但它们依然很难和更高级的概念相对应。
CAV(概念激活向量)的核心思想是度量模型输出中概念的相关性。对概念来说,CAV 是概念示例集的值方向上的一个向量。在他们的论文中,谷歌研究团队还提到了一种名为 TCAV(Testing with CAV)的新型线性可解释性方法,这种方法用方向导数(directional derivatives)来量化模型预测对 CAV 学习到的底层高级概念的敏感度。
TCAV 方法分为三个基本步骤:
- 给模型定义相关概念;
- 理解预测结果对这些概念的敏感度;
- 全局定量解释每个概念对每个模型预测类的相对重要性。
TCAV可以看作是添加了人为定义的概念作为约束,进一步提升了人类理解上的可解释。

