Kmean聚类算法原理python实现
Kmean聚类算法原理python实现
Kmean聚类算法是基于距离对对象进行分类的算法,该算法实现步骤如下:
1、确定初始数据簇质心,质心的数量与需要分的类的数量一致;
2、将数据集中的每一个对象与不同质心计算距离,并将其分类到最近的质心簇中;
3、更新数据簇质心,迭代计算,直到数据簇质心不再变化或者分类精度达到要求时,停止算法。
代码如下:
(1)创建数据集代码:
import matplotlib.pyplot as plt
import numpy as np
import random
def make_data():
data_list = []
data_list1 = []
data_list2 = []
data_list3 = []
for _ in range(30):
data1 = []
data2 = []
data3 = []
for _ in range(4):
data1.append(random.randint(0, 10))
data2.append(random.randint(15, 30))
data3.append(random.randint(55, 70))
data_list1.append(data1)
data_list2.append(data2)
data_list3.append(data3)
data_list.append(data1)
data_list.append(data2)
data_list.append(data3)
return data_list, data_list1, data_list2, data_list3
if __name__ == '__main__':
data, _, _, _ = make_data()
# print(data)
data_x = []
data_y = []
for i in data:
print(i)
data_x.append(np.sqrt(i[0] ** 2 + i[1] ** 2 + i[2] ** 2))
data_y.append(i[3])
plt.scatter(data_x, data_y)
plt.show()
(2)Kmean算法实现分类
# kmean算法原理演示
import numpy as np
import matplotlib.pyplot as plt
import creat_data
import sys
sys.setrecursionlimit(1000000)
def kmean_test(cornel_list, data_list):
"""
:param data_list: [[],[],[],[],...,[]]
:param cornel_list: [[],[],[],...,[]],内部元素数量与需要分类的个数有关
:return: 新内核[[],[],[],...,[]]和分类的数据[[[],[],...,],[[],[],...,],...,]
"""
table_list = []
for _ in cornel_list:
table_list.append([])
# 将列表转换为numpy数组
data_list_array = np.array(data_list)
cornel_list_array = np.array(cornel_list)
for data_item in data_list_array:
distance_list = []
for cornel_item in cornel_list_array:
distance = np.sqrt(np.sum((data_item - cornel_item) ** 2))
distance_list.append(distance)
min_value_index = distance_list.index(min(distance_list))
table_list[min_value_index].append(data_item.tolist())
table_list_array = np.array(table_list)
# 计算新核
new_cornel_list = []
for table in table_list_array:
sum_cornel = np.zeros((1, len(data_list_array[0])))
for item in table:
sum_cornel += item
new_cornel_list.append((sum_cornel / len(table)).tolist())
KM.cornel_list_a = new_cornel_list
KM.table_list_b = table_list
return table_list, new_cornel_list
class KM:
cornel_list_a = None
table_list_b = None
def __init__(self, a, b):
self.count = 0
self.loop(a, b)
def loop(self, cornel_list, data_list):
table, new_cornel = kmean_test(cornel_list, data_list)
if new_cornel == cornel_list:
# print("迭代%d次寻找到最佳分组如下:" % self.count)
# for table0 in table:
# for item in table0:
# print(item)
# print("#################")
return table, new_cornel
else:
self.count += 1
self.loop(new_cornel, data_list)
if __name__ == '__main__':
km = KM
data, list1, list2, list3 = creat_data.make_data()
list1_x = []
list1_y = []
list2_x = []
list2_y = []
list3_x = []
list3_y = []
for i in list1:
list1_x.append(np.sqrt(i[0] ** 2 + i[1] ** 2 + i[2] ** 2))
list1_y.append(i[3])
for j in list2:
list2_x.append(np.sqrt(j[0] ** 2 + j[1] ** 2 + j[2] ** 2))
list2_y.append(j[3])
for k in list3:
list3_x.append(np.sqrt(k[0] ** 2 + k[1] ** 2 + k[2] ** 2))
list3_y.append(k[3])
cornel_list1 = [[1, 3, 4, 5], [5, 6, 2, 3], [5, 3, 8, 4]]
km(cornel_list1, data)
cornel1 = km.cornel_list_a
table1 = km.table_list_b
cornel_list0 = [[40, 10, 36, 5], [33, 55, 74, 21], [9, 13, 18, 4]]
km(cornel_list0, data)
cornel2 = km.cornel_list_a
table2 = km.table_list_b
init_cornel1_x = []
init_cornel1_y = []
init_cornel2_x = []
init_cornel2_y = []
cornel1_x = []
cornel1_y = []
cornel2_x = []
cornel2_y = []
for h in cornel_list1:
init_cornel1_x.append(np.sqrt(h[0] ** 2 + h[1] ** 2 + h[2] ** 2))
init_cornel1_y.append(h[3])
for h1 in cornel_list0:
init_cornel2_x.append(np.sqrt(h1[0] ** 2 + h1[1] ** 2 + h1[2] ** 2))
init_cornel2_y.append(h1[3])
for i in cornel1:
cornel1_x.append(np.sqrt(i[0][0] ** 2 + i[0][1] ** 2 + i[0][2] ** 2))
cornel1_y.append(i[0][3])
for j in cornel2:
cornel2_x.append(np.sqrt(j[0][0] ** 2 + j[0][1] ** 2 + j[0][2] ** 2))
cornel2_y.append(j[0][3])
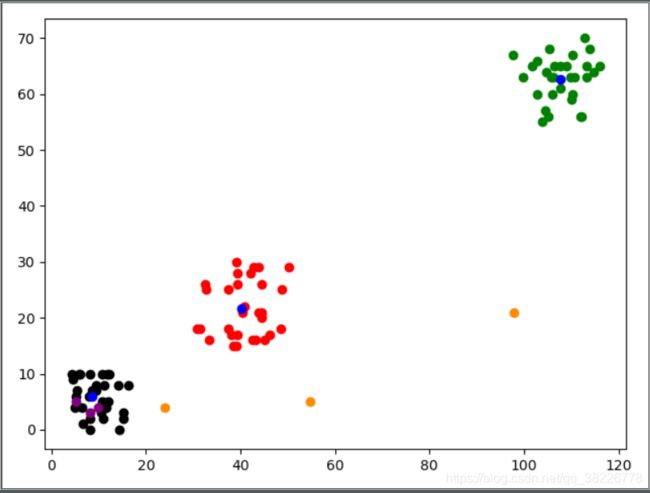
plt.scatter(list1_x, list1_y, color='black')
plt.scatter(list2_x, list2_y, color='red')
plt.scatter(list3_x, list3_y, color='green')
plt.scatter(cornel1_x, cornel1_y, color='blue')
plt.scatter(cornel2_x, cornel2_y, color='yellow')
plt.scatter(init_cornel1_x, init_cornel1_y, color='purple')
plt.scatter(init_cornel2_x, init_cornel2_y, color='darkorange')
plt.show()
运行结果如下:
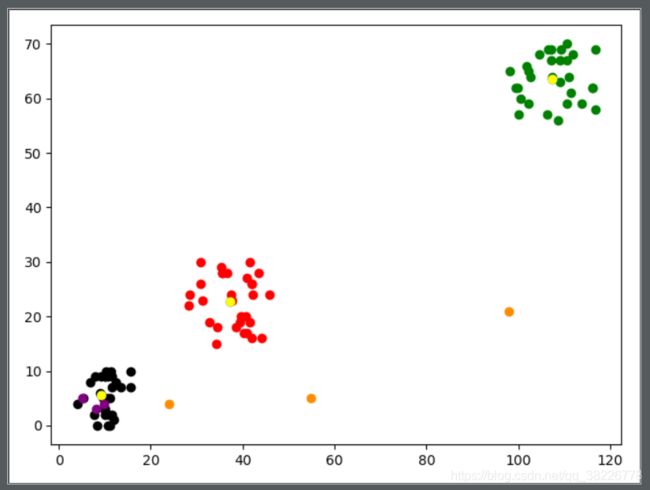
图中用不同颜色标记不同数据点,黑色、红色和绿色分别是不同簇的数据,橙色和紫色为初始设置的质心(初始设置了两个不同的质心,分别对同一组数据进行分类,以说明初始质心的选择对分类结果的影响。)黄色和蓝色分别为初始质心确定的最终分类质心的结果,由于初始两个质心最终确定的分类质心相同,导致蓝色质心被覆盖。当对其中一个最终质心不描绘时,就可以看到另一个蓝色质心了,如下: