基于Iterative映射和非线性拟合的鲸鱼优化算法
文章目录
- 一、理论基础
-
- 1、鲸鱼优化算法
- 2、改进的鲸鱼优化算法
-
- (1)Iterative映射初始化
- (2)非线性拟合的收敛因子和惯性权重
- (3)NWOA算法流程图
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、鲸鱼优化算法
请参考这里。
2、改进的鲸鱼优化算法
(1)Iterative映射初始化
WOA算法采用随机生成的方式来初始化种群。然而,这种方式可能会破坏种群的多样
性。研究表明混沌序列具有很好的随机性和遍历性,因此本文采用Iterative映射的方法对种群进行初始化,其方程式如下 x i + 1 = sin ( b π x i ) (1) x_{i+1}=\sin\left(\frac{b\pi}{x_i}\right)\tag{1} xi+1=sin(xibπ)(1)其中, b ∈ [ 0 , 1 ] b\in[0,1] b∈[0,1],本文取值为 b = 0.5 b=0.5 b=0.5。
(2)非线性拟合的收敛因子和惯性权重
本文采用非线性拟合的策略调控收敛因子 a a a,表达式为 a ( t ) = − μ ⋅ log ( t / M a x _ i t e r ) (2) a(t)=-\mu\cdot\log\left(t/Max\_iter\right)\tag{2} a(t)=−μ⋅log(t/Max_iter)(2)其中, t t t为当前迭代次数, M a x _ i t e r Max\_iter Max_iter为最大迭代次数, μ \mu μ是一个常数。
受粒子群算法中惯性权重的启发,本文提出一种基于非线性拟合的惯性权重,其数学模型如下 w ( t ) = − ( w max − w min ) ⋅ t η + w min (3) w(t)=-(w_{\max}-w_{\min})\cdot t^\eta+w_{\min}\tag{3} w(t)=−(wmax−wmin)⋅tη+wmin(3)其中, w max w_{\max} wmax和 w min w_{\min} wmin分别为惯性权重的最大值和最小值, η \eta η是一个常数参数。
更新之后的位置更新公式为 L ( t + 1 ) = w ⋅ L ∗ ( t ) − A ⋅ D (4) L(t+1)=w\cdot L^*(t)-A\cdot D\tag{4} L(t+1)=w⋅L∗(t)−A⋅D(4) L ( t + 1 ) = w ⋅ L ∗ ( t ) − D ′ ⋅ e b l ⋅ cos ( 2 π l ) (5) L(t+1)=w\cdot L^*(t)-D'\cdot e^{bl}\cdot\cos(2\pi l)\tag{5} L(t+1)=w⋅L∗(t)−D′⋅ebl⋅cos(2πl)(5)
(3)NWOA算法流程图
在WOA算法的基础上,根据上述两方面改进了该算法。改进后的算法流程图如图1所示。

二、仿真实验与结果分析
将提出的NWOA算法与基本WOA算法和EWOA算法[2]进行对比,种群规模为30,最大迭代次数为500,每个算法独立运行50次,以文献[1]中表1的F3~F5(单峰/30维)、F10~F12(多峰/30维)为例。
结果显示如下:





函数:F3
WOA:最差值: 62778.735,最优值:18296.8035,平均值:44200.012,标准差:10511.9817
EWOA:最差值: 4.7397e-164,最优值:8.9189e-241,平均值:9.4795e-166,标准差:0
NWOA:最差值: 0,最优值:0,平均值:0,标准差:0
函数:F4
WOA:最差值: 88.8641,最优值:9.084e-05,平均值:42.5267,标准差:28.0707
EWOA:最差值: 6.8794e-93,最优值:2.1478e-124,平均值:2.5974e-94,标准差:1.0232e-93
NWOA:最差值: 0,最优值:0,平均值:0,标准差:0
函数:F5
WOA:最差值: 4.6217e-144,最优值:2.7675e-175,平均值:1.798e-145,标准差:8.8953e-145
EWOA:最差值: 0,最优值:0,平均值:0,标准差:0
NWOA:最差值: 0,最优值:0,平均值:0,标准差:0
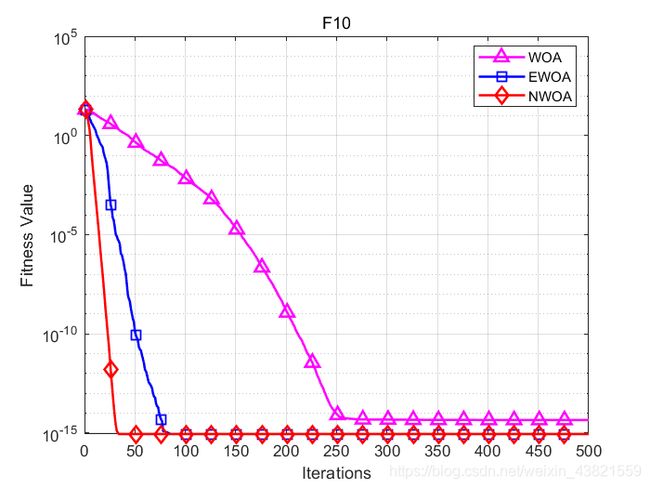
函数:F10
WOA:最差值: 7.9936e-15,最优值:8.8818e-16,平均值:4.5119e-15,标准差:2.2111e-15
EWOA:最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0
NWOA:最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0
函数:F11
WOA:最差值: 0.17588,最优值:0,平均值:0.0035176,标准差:0.024873
EWOA:最差值: 0,最优值:0,平均值:0,标准差:0
NWOA:最差值: 0,最优值:0,平均值:0,标准差:0
函数:F12
WOA:最差值: 0.043371,最优值:1.6813e-08,平均值:0.006283,标准差:0.0079899
EWOA:最差值: 0.042565,最优值:1.9314e-07,平均值:0.0058794,标准差:0.0070446
NWOA:最差值: 0.030029,最优值:1.9198e-05,平均值:0.0065448,标准差:0.0062094
结果表明,NWOA算法与WOA和EWOA算法相比,寻优精度显著提高且稳定性较强。
三、参考文献
[1] 李赛宇, 鞠传香, 丁航奇. 基于Iterative映射和非线性拟合的鲸鱼优化算法[J/OL]. 重庆大学学报: 1-17 [2021-08-20].
[2] 钟明辉, 龙文. 一种随机调整控制参数的鲸鱼优化算法[J]. 科学技术与工程, 2017, 17(12): 68-73.